一种滚动轴承-转子系统非线性响应不确定性量化方法

本发明属于滚动轴承-转子系统领域，具体涉及一种滚动轴承-转子系统非线性响应不确定性量化方法。

背景技术：

1、传统滚动轴承的设计和分析大多基于确定性的模型，即分析对象的参数始终保持一致而不存在波动性。事实上，工程中复杂机械系统不可避免地存在各类不确定性因素。在滚动轴承中，不确定性存在于其生命的整个周期，包含设计、制造到安装、服役等各个阶段。零件加工误差、安装间隙、材料分布不均匀、以及接触界面之间的磨损等，都是典型的不确定性源，均会造成滚动轴承的动力学行为呈现非确定特性。不确定性会导致原本符合要求的设计方案失效，甚至出现毁灭性的事故。因此，对滚动轴承在考虑不确定性时的动力学行为进行研究和评估，以准确估计不确定性的影响，对于避免重大安全事故并提升效益具有重要意义。

2、目前，传统的滚动轴承不确定性量化方法存在以下两方面的缺陷：第一，在工程问题中，往往不是所有不确定性参数都包含足够的统计信息，也不是都没有任何先验认知。即它们部分可用随机变量来建模，部分则必须用非概率区间变量来描述。当前，绝大部分针对以上问题的研究采用单-的非概率方法。然而，在以上情形下，已有的部分认知信息被忽略，未充分利用有利条件，不能获得更为精细的不确定性分析结果；第二，传统滚动轴承在进行考虑非线性因素的响应分析时，常采用时域积分或牛顿迭代法，计算时间长，且无法获得完整的幅频响应曲线，求解效果差。

3、综上，需要开发一种滚动轴承-转子系统非线性响应不确定性高精度量化方法。

技术实现思路

1、要解决的技术问题：

2、为了避免现有技术的不足之处，本发明提供一种滚动轴承-转子系统非线性响应不确定性量化方法，在滚动轴承-转子系统的振动模型基础上，考虑混合不确定性，并分别开展考虑随机参数和区间参数的动力学特性分析，得到滚动轴承-转子系统非线性动力学响应的均值区间和方程区间，及完成不确定性量化；其中结合打靶法、弧长法、多项式代理模型等方法，针对滚动轴承的非线性稳态响应，建立代理模型，评估非线性响应的不确定性，解决了现有技术中计算时间长且不确定性分析结果精度低的问题。

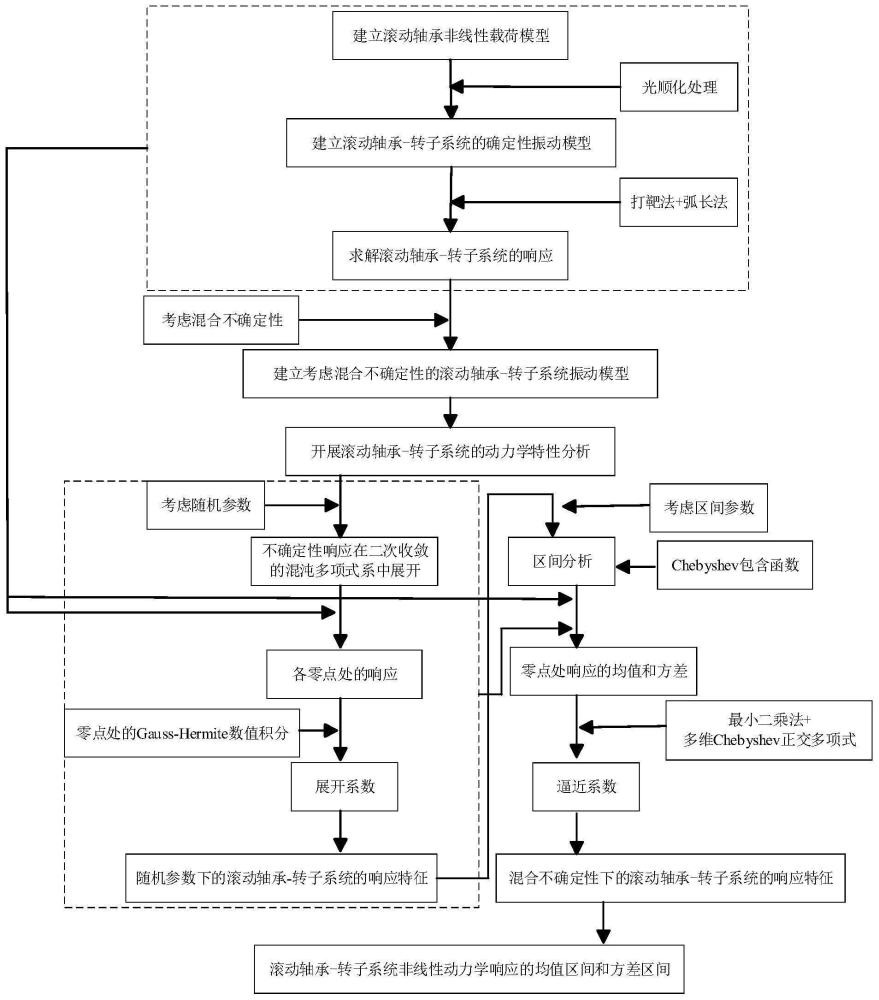
3、本发明的技术方案是：一种滚动轴承-转子系统非线性响应不确定性量化方法，具体步骤如下：

4、建立滚动轴承非线性载荷模型；

5、对所述滚动轴承非线性载荷模型进行光顺化处理，得到滚动轴承非线性载荷的光滑模型；

6、将所述滚动轴承非线性载荷的光滑模型加入转子振动模型中，得到滚动轴承-转子系统的确定性振动模型；并求解滚动轴承-转子系统的响应；

7、在所述滚动轴承-转子系统的确定性振动模型的基础上，考虑混合不确定性，得到考虑混合不确定性的滚动轴承-转子系统振动模型；

8、对考虑混合不确定性的滚动轴承-转子系统振动模型开展考虑随机参数的滚动轴承-转子系统的动力学特性分析，得到随机参数下的滚动轴承-转子系统的响应特征；

9、对所述随机参数下的滚动轴承-转子系统的响应特征开展考虑区间参数的滚动轴承-转子系统的动力学特性分析，得到混合不确定性下的滚动轴承-转子系统的响应特征；

10、获得滚动轴承-转子系统非线性动力学响应的均值区间和方差区间，即完成滚动轴承-转子系统非线性响应不确定性量化。

11、本发明的进一步技术方案是：所述滚动轴承包括多个滚动体，当滚动体与滚道的接触变形量≤0时，滚动轴承产生的轴承载荷为0；当滚动体与滚道的接触变形量＞0时，滚动轴承产生在x和y轴向上的轴承载荷。

12、本发明的进一步技术方案是：所述光顺化处理方法为，将由于部分滚动体与滚道接触产生变形量、部分滚动体与滚道不接触不产生变形量得到的分段函数采用可导函数表示，即将连续但不可导的分段非线性力处理为连续且可导的力，，便于非线性求解。

13、本发明的进一步技术方案是：所述滚动轴承-转子系统的响应的求解方法为，首先假设滚动轴承-转子系统的响应具有周期性特点，即滚动轴承-转子系统的位移和速度向量满足周期性条件；然后，对滚动轴承-转子系统的响应进行预测，根据已有的状态对下一状态解进行预估，得到预估解；之后，将预估解通过逐步校正的方式，使其接近正确的状态解,校正过程需满足校正方向与预测方向相垂直的条件，反复迭代得到收敛的状态解，即得到滚动轴承-转子系统的响应。

14、本发明的进一步技术方案是：所述滚动轴承-转子系统的确定性振动模型为：

15、

16、式中，m为质量矩阵；c为阻尼矩阵；k为刚矩阵；fext为外部振力向量；fbrn为轴承载荷向量，fbrn为滚子轴承的载荷，u为位移向量；

17、所述滚动轴承-转子系统的响应满足以下收敛条件时，即得到满足要求的响应：

18、

19、式中，ε为迭代收敛容差，为位移向量，i为迭代步数。

20、本发明的进一步技术方案是：所述考虑混合不确定性的滚动轴承-转子系统振动模型为：

21、

22、式中，abi＝[a；bi]代表系统存在的所有不确定性，a为随机变量，bi为区间变量。

23、本发明的进一步技术方案是：所述开展考虑随机参数的滚动轴承-转子系统的动力学特性分析的方法为：

24、将所述考虑混合不确定性的滚动轴承-转子系统振动模型中的不确定性响应在二次收敛的混沌多项式系中展开；

25、将随机参数替换为零点参数代入所述滚动轴承-转子系统的确定性振动模型，并进行求解得到各零点处的确定性响应；

26、结合零点处的gauss-hermite数值积分，计算所述二次收敛的混沌多项式的展开系数；

27、获得随机参数下的滚动轴承-转子系统的不确定性响应特征。

28、本发明的进一步技术方案是：所述随机参数下的滚动轴承-转子系统的不确定性响应的均值和方差表示为：

29、

30、式中，μ为均值，σ为方差，为两个相同混沌项乘积的期望。

31、本发明的进一步技术方案是：所述开展考虑区间参数的滚动轴承-转子系统的动力学特性分析的方法为：

32、采用chebyshev包含函数对所述滚动轴承-转子系统的不确定性响应特征开展区间分析，分别建立随机响应中均值和方差的代理函数y1和y2；

33、将区间参数替换为零点参数代入所述滚动轴承-转子系统的确定性振动模型，并进行求解得到各零点处的确定性响应；

34、采用所述开展考虑随机参数的滚动轴承-转子系统的动力学特性分析的方法，获得区间参数下的滚动轴承-转子系统的响应随机特征，即零点处响应的均值和方差；

35、通过最小二乘法计算chebyshev包含函数中的展开系数；

36、获得区间参数下的滚动轴承-转子系统的不确定性响应特征。

37、本发明的进一步技术方案是：所述区间参数下的滚动轴承-转子系统的不确定性响应的均值和方差表示为：

38、

39、式中，l表示下限，u表示上限。

40、有益效果

41、本发明的有益效果在于：

42、(1)本发明对滚动轴承非线性载荷模型进行了光顺化处理，避免了分段函数连续不可导特性所导致滚动轴承-转子系统非线性响应求解容易发散的问题，提高了求解方法的稳定性。

43、(2)本发明采用打靶法和弧长法相结合的方法求解滚动轴承-转子系统非线性响应，一方面打靶法无需假设解的形式，避免了谐波平衡法的分析结果依赖谐波截断阶数、假设级数形式的问题，另一方面，弧长法的引入可以保证打靶法能够追踪非线性系统中的多解现象/跳跃现象，拓宽了数值方法的适用性。

44、(3)本发明考虑了工程实际中的不确定性因素，使得求解结果的覆盖范围较传统确定性设计更广，使得设计阶段对安全性的考虑更加完备。而且，本发明同时考虑了不确定性参数中的概率信息和非概率信息，未舍去不确定性因素的统计信息，可以获得更为精细、更符合工程实际情况的不确定性分析结果。

45、(4)基于该项发明提供的方法，可以有效评估滚动轴承的非线性响应不确定性量化，加深对滚动轴承-转子系统运行可靠性的理解，提高其设计水平。