基于时间序列预测与深度学习互补的短期负荷预测方法与流程

本技术涉及负荷预测，尤其涉及一种基于时间序列预测与深度学习互补的短期负荷预测方法。

背景技术：

1、智能电网的高速发展对电力负荷预测精度的要求与日俱增，精准的电力负荷预测为电力系统的规划调度、经济运行提供了重要依据。电力负荷短期预测可以在满足用户需求的前提下，有效地保障系统安全运行，指导电力调度计划，提高电网运行效益。但是，短期电力负荷受诸多不确定性因素影响，负荷时间序列呈非平稳的随机过程，预测难度较大。电力负荷预测实质是时间序列预测问题，存在非平稳性和影响因素的复杂性。因此，针对如何提高短期电力负荷预测精度的研究具有十分重要的意义。

技术实现思路

1、针对上述存在的技术问题，本发明的目的在于解决ari ma在光伏负荷序列预测中存在两方面的不足：在使用差分整合移动平均自回归法(ari ma)进行短期电力负荷预测时，电力负荷数据可使用线性和非线性成分叠加表示。为弥补传统ari ma时间序列预测法忽略非线性的缺陷，引入了长短时记忆神经网络(lstm)挖掘数据残差非线性规律。为解决负荷数据序列因非平稳特性而导致难以预测的问题，本发明提供一种基于时间序列预测与深度学习互补的短期负荷预测方法。通过改进蜣螂优化算法优化ari ma模型，利用改进后的蜣螂优化算法对差分整合移动平均自回归模型参数p和q进行定阶，实现对短期负荷的预测。并将lstm预测残差与ari ma预测结果相叠加重构，达到更高的精度。

2、鉴于短期电力负荷的预测时间的间隔较短、气象条件变化不显著，本发明在开展预测工作时仅考虑电力负荷历史数据。

3、本发明的目的是通过以下技术方案来实现的：

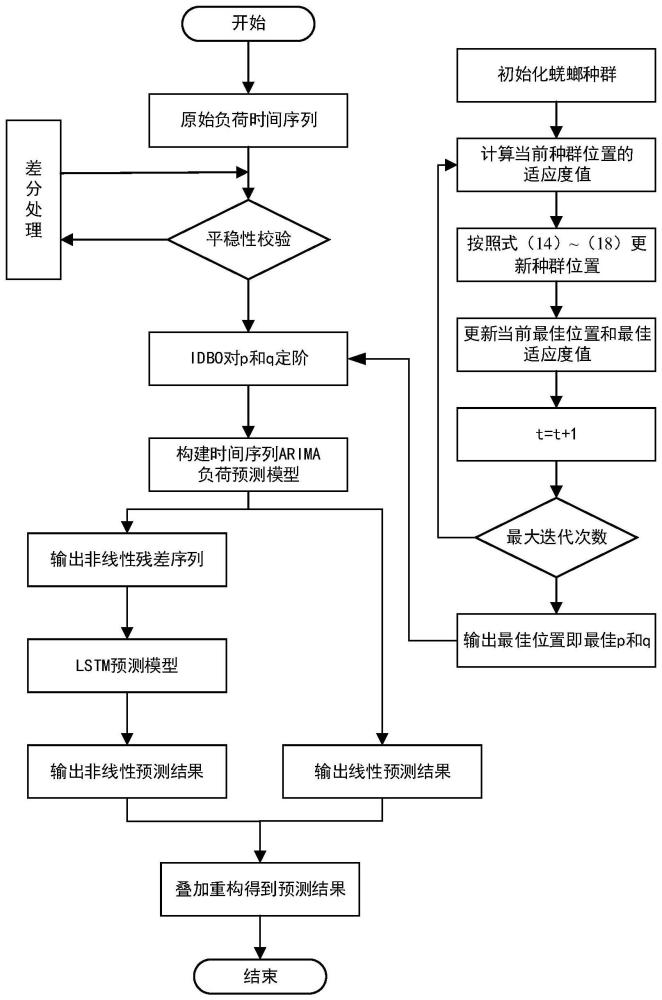
4、本发明一种基于时间序列预测与深度学习互补的短期负荷预测方法，包括如下步骤：

5、s1：对多元历史负荷数据样本序列进行平稳性检验，得到的平稳序列数据进行步骤s3；

6、s2：对所述步骤1中不平稳的数据，进行差分运算，得到平稳的序列数据进行步骤s3；

7、s3：由所述步骤s1和s2中得到的平稳数据，通过改进的蜣螂优化算法对arima模型的参数p和q定阶；

8、s4：根据s3中的参数p和q构建idbo-arima模型，由所述idbo-arima模型，对负荷序列进行短期预测，得到线性序列和非线性序列；

9、s5：由所述步骤s4中的idbo-arima模型预测后的非线性序列，使用lstm网络对其进行预测，得到非线性序列结果；

10、s6：由所述步骤s4和步骤s5中的负荷序列预测结果，将线性预测和非线性预测叠加重构，得到短期负荷预测的结果。

11、进一步地，所述步骤s1中对多元历史负荷数据样本序列进行平稳性检验，采用adf与kpss联合检验。

12、进一步地，所述步骤s1中的差分运算是将非平稳的时间序列进行平稳化的运算方法，通过差分运算使序列转换为平稳序列为止。

13、进一步地，所述步骤s2中的改进的蜣螂优化算法，是引入周期性突变机制，使改进后的优化算法在解空间中能够进行较大范围的周期性跳跃，以实现算法更为充分的寻优。

14、进一步地，所述周期性突变机制如下式所示：

15、xi(t+1)＝xi(t)×[1+a×(0.5-rand)×σ]

16、

17、式中：a为突变幅度；rand表示按照均匀分布n(0，1)随机生成的实数；t为突变周期，其值小于最大迭代次数；σ是根据突变周期从一个区域搜索到另一个区域的冲量。

18、进一步地，得到的改进后的优化算法:

19、在滚球行为中，蜣螂的位置进行更新为：

20、

21、式中：t表示当前的迭代次数；xi(t)为第i只蜣螂在第t次迭代中的位置信息；k为偏转系数，取值范围为(0，0.2]；b为一个常数，取值范围为(0，1)；a为自然系数，取值1或者-1，1表示无偏差，-1表示偏离原来方向；xworst表示全局最差的蜣螂位置；△x用于模拟光强的变化；

22、在跳舞行为中，蜣螂的位置进行更新为：

23、

24、式中：θ为偏转角，取值范围为[0，π]，当θ＝0，π/2或π时，蜣螂的位置不进行更新；

25、在繁殖行为中，卵球的位置变化为：

26、

27、式中：bi(t)为第i个卵球在第t次迭代时的位置信息；b1和b2表示两个大小为1×d的独立随机向量，d表示优化问题的维数；

28、在觅食行为中，蜣螂的最佳觅食区域以及觅食过程中的位置变化为：

29、

30、式中：xb表示全局最优位置；lb和ub为最佳觅食区域的下界和上界；xi(t)表示第i只小蜣螂在第t次迭代中的位置信息；c1表示遵循正态分布的随机数；c2表示(0，1)范围内的随机向量；

31、在偷窃行为中，小偷蜣螂的位置更新为：

32、

33、式中：xi(t)为第i个小偷蜣螂在第t次迭代时的位置信息，g为大小为1xd的服从正态分布的随机向量，s为常数值；

34、以贝叶斯信息准则评价，并将其最小值作为idbo算法的适应度函数，bic的数值计算公式如下：

35、bic＝-2×ln(l)+(p+q+1)×ln(n)

36、式中：l为似然函数；n为样本数量；p和q分别是自回归项阶数和移动平均项阶数。

37、进一步地，所述步骤s3中对arima模型的参数p和q定阶，通过改进后的蜣螂优化算法对arima模型进行定阶，设置蜣螂种群为30个，其中，滚球和跳舞蜣螂6个，繁殖蜣螂6个，觅食蜣螂7个，小偷蜣螂11个，以概率的方式分别进行滚球行为和跳舞行为，具体方法为：在0～1之间取一个随机数，若小于0.9，则进行滚球行为，否则进行跳舞行为；在滚球行为中的a取值同样采用概率的方式，若随机数大于0.1，a取值1，否则取值-1；偏转系数k取值0.1；参数b取值0.3；参数s取值0.5；突变幅度a取值1；突变周期t取值5；选取bic的最小数值为算法的适应度函数；通过训练得到最优阶数p和q。

38、进一步地，所述步骤s4中，通过所述步骤s3中的最优阶数构建idbo-arima模型,对线性负荷序列进行短期预测，以时间序列分析方法中的arima模型为基础，运用所建立的模型以及现在、过去的时间序列的观测值，求出对未来时间序列的最佳预测值；

39、其中，arima模型通常写作arima(p，d，q)，给定一维电力负荷时间序列，对其进行d次差分处理后得到平稳序列xt(t＝1,2,…,n)，然后将该平稳序列线性拟合为arma(p，q)模型，模型的表达式为

40、

41、式中：p和q分别为自回归阶数、滑动平均阶数；εt为白噪声序列；为自回归系数；θ1,…,θq为滑动平均系数。

42、进一步地，所述步骤s5中使用lstm网络对其非线性序列进行预测，arima模型的残差是lstm机器学习模型的输入，得到预测非线性数据计算公式为：

43、l＝f(△f1,△f2,△f3,…,△fn)

44、式中：f(…)为lstm的非线性建模，△f1,△f2,△f3,…,△fn为拟合残差序列。

45、进一步地，对所述步骤s6中得到的短期负荷预测结果进行性能评价，采用均方根误差、平均绝对误差、平均绝对百分比误差以及确定系数(r2)4类指标评价idbo-arima-lstm预测模型的准确性；4类指标的计算公式分别如下式所示：

46、

47、

48、

49、

50、式中：为预测值；xi为实际值；为实际样本的平均值。

51、本发明的有益效果为：

52、1.本发明的预测方法，通过adf检验和kpss检验对历史负荷数据序列进行平稳性检验，若不平稳则进行差分处理直至信号平稳。再通过在蜣螂优化算法中引入周期突变机制以提升算法的寻优能力，并利用改进后的蜣螂优化算法对差分整合移动平均自回归模型参数p和q进行定阶，实现arima对负荷的预测。然后，使用lstm将arima预测的非线性的残差序列进行预测。最后，将得到的负荷预测结果进行校验，大幅度提升模型的预测准确率，得到更为精确的短期负荷预测结果。

53、2.本发明通过改进蜣螂优化算法优化arima模型，利用改进后的蜣螂优化算法对差分整合移动平均自回归模型参数p和q进行定阶，实现对短期负荷的预测。并将lstm预测残差与ari ma预测结果相叠加重构，达到更高的精度。