基于非连续壳-弹簧模型的盾构管片安全评估方法

本发明涉及盾构隧道结构安全评估，尤其涉及一种基于非连续壳-弹簧模型的盾构管片安全评估方法。

背景技术：

1、随着城市轨道交通里程的增加和城市的快速发展，附近建设活动造成的弃土现象越来越普遍，地面堆土会增加盾构管片内力与变形，从而降低了盾构隧道结构安全稳定性。因此，为保障盾构隧道结构安全，对盾构管片进行安全性评估显得十分必要。

2、目前，关于盾构管片结构的安全性评估，还没有统一的计算模型，常用的方法有惯用法、修正惯用方法、多铰圆环法、梁-弹簧模型法。不同模型计算的盾构管片结构内力及变形不同，从而对盾构管片结构设计与工程造价造成较大影响。目前大多采用一维曲梁单元模拟盾构管片，假设盾构管片环为平面应变状态，但在盾构管片错缝拼装的条件下，盾构管片的应力状态为非平面应变状态，认为梁单元上某一点的应力集中对盾构管片宽度方向均有影响，实际上是夸大了局部的加强效应，因此采用一维曲梁单元模拟盾构管片并不能充分反映错缝拼装条件下盾构管片的真实应力状态，无法准确地计算盾构管片结构在地层中的结构力学响应特征。

3、申请号为cn202310741374.8的发明公开了一种地铁错缝盾构隧道的结构安全评估方法，包括以下步骤：步骤1：建立安全评估参考标准；步骤2：查询评估区间隧道的地层抗力系数；步骤3：利用grp5000移动式激光扫描测量系统每间隔4-6个月对评估区间隧道进行连续扫描一次，获得评估区间隧道最新的现实隧道椭圆度；步骤4：根据步骤2步骤3得到的信息，对照步骤1中的安全评估参考标准得出安全评价结果。但上述结构安全评估方法对盾构隧道整体的椭圆度进行检测，不能准确模拟盾构管片真实受力情况，不能充分反映错缝拼装条件下盾构管片的真实应力状态。

技术实现思路

1、本发明的目的在于为解决现有技术中的缺陷，而提供一种基于非连续壳-弹簧模型的盾构管片安全评估方法，解决了现有计算模型不能准确模拟盾构管片真实受力情况，不能充分反映错缝拼装条件下盾构管片的真实应力状态，无法准确地计算错缝盾构管片结构在地层中的结构力学响应特征，难以准确评估地层中盾构管片安全性的问题。

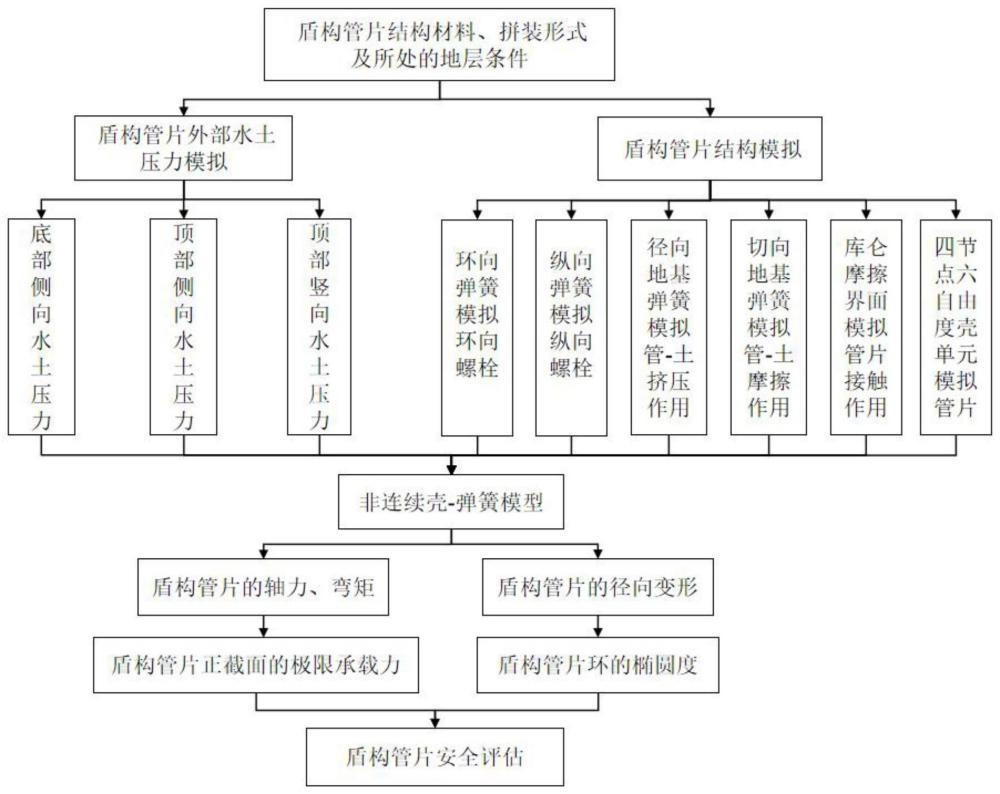
2、为实现上述目的，本发明提供基于非连续壳-弹簧模型的盾构管片安全评估方法，包括以下步骤：

3、s1、根据盾构管片的结构材料、拼装形式和结构尺寸，及盾构管片所处地层条件，得到盾构管片环和盾构管片的物理参数；

4、s2、根据步骤s1中得到的盾构管片环和盾构管片的物理参数建立非连续壳-弹簧模型；

5、s3、根据盾构管片所处地层条件得到盾构管片的外部水土压力，将盾构管片的外部水土压力施加在非连续壳-弹簧模型上，得到盾构管片环不同角度的轴力、弯矩和径向位移；

6、s4、计算盾构管片正截面的极限承载力，根据步骤s3中盾构管片环不同角度的轴力和弯矩，确定盾构管片的最不利正截面，并根据最不利正截面的轴力和弯矩，得到最不利正截面的极限承载力；

7、s5、根据步骤s4中最不利正截面的极限承载力和轴力，得到盾构管片的极限承载力安全系数，判定盾构管片的承载力安全等级；

8、s6、根据步骤s3中径向位移，得到盾构管片环的水平收敛值和竖向收敛值，根据盾构管片环的水平收敛值和竖向收敛值得到盾构管片环的椭圆度，判断盾构管片环变形是否在安全范围之内。

9、本发明提出了基于非连续壳-弹簧模型的盾构管片安全评估方法，非连续壳-弹簧模型不仅能模拟盾构管片间的错缝拼装形式，还能反映盾构管片结构螺栓处局部的应力集中现象以及横、纵向结构力学响应，较真实地反映了盾构管片的实际受力情况。

10、非连续壳-弹簧模型具有建模简单、计算效率高、能更好地模拟盾构管片的应力状态等优点，运用非连续壳-弹簧模型可以更全面的反映盾构隧道衬砌盾构管片的力学性态，以准确地计算盾构管片结构在地层中的结构力学响应特征，准确评估地层中盾构管片安全性的问题。

11、可选的，所述非连续壳-弹簧模型包括盾构管片结构模型与盾构管片外部水土压力。

12、可选的，所述盾构管片结构模型包括环向弹簧、纵向弹簧、地基弹簧、库仑摩擦界面以及四节点六自由度的壳单元，所述地基弹簧包括径向地基弹簧与切向地基弹簧。

13、可选的，所述步骤s3中，盾构管片的外部水土压力包括外部土压力和外部水压力，所述外部土压力包括顶部竖向土压力、顶部侧向土压力与底部侧向土压力，所述外部水压力包括盾构管片环顶部水压力、盾构管片环底部水压力。

14、可选的，所述外部土压力的计算公式为：

15、

16、

17、

18、

19、

20、其中，p1为顶部竖向土压力(kpa)；p2为顶部侧向土压力(kpa)；p3为底部侧向土压力(kpa)；rc为盾构管片环半径(m)；b为隧道围岩自然拱的净宽(m)；h为盾构管片埋深(m)；γ为土层平均重度(kpa/m)；c为土层平均粘聚力(kpa)；为土层平均内摩擦角(°)；hi为土层厚度(m)；γi为土层重度(kpa/m)；ci为土层粘聚力(kpa)；为土层内摩擦角(°)；k为侧压力系数；q为地面荷载(kpa)。

21、可选的，所述外部水压力公式为：

22、pw1＝λ×γw×hw

23、pw2＝λ×γw×(hw+2rc)

24、其中，pw1为盾构管片环顶部水压力(kpa)；pw2为盾构管片环底部水压力(kpa)；λ为地层渗透系数；γw为水的重度(kpa/m)；hw为地下水到盾构管片环顶部的距离(m)。

25、可选的，步骤s4中盾构管片最不利的正截面确定公式为：

26、

27、其中，ekmax为盾构管片正截面最大偏心距(mm)；mk为盾构隧道k角度管片的正截面弯矩(kn·m)，nk为盾构隧道k角度管片的正截面轴力(kn)。

28、可选的，步骤s4中盾构管片正截面的极限承载力计算包括大偏心受压与小偏心受压判断、大偏心受压极限承载力计算与小偏心受压极限承载力计算。

29、可选的，所述大偏心受压与小偏心受压判断的公式为：

30、

31、h0＝h-as

32、

33、若e0＞e0b，则为大偏心受压；若e0＜e0b，则为小偏心受压；

34、其中，e0为轴向力对截面重心轴的偏心距(mm)；e0b为界限偏心距(mm)；h为截面高度(mm)；b为截面宽度(mm)；h0为截面有效高度(mm)；ξb为相对界限受压区高度；as'为盾构管片受压主筋合力点至截面受压区边缘距离(mm)；as为盾构管片受拉主筋合力点至受拉边缘距离(mm)；fy为主筋抗拉强度(kpa)、fy'为主筋抗压强度(kpa)；fc为盾构管片混凝土抗压强度(kpa)；as为受拉主筋截面面积(mm2)、as'为受压主筋截面面积(mm2)；m为弯矩(kn·m)；n为轴力(kn)；

35、所述轴向力作用点至受拉主筋合力点之间的距离的计算公式为：

36、

37、l0＝0.54·l

38、

39、ei＝e0+ea

40、

41、

42、e1＝η·ei+h/2-as

43、其中，η为偏心增大系数；l0为计算长度(mm)；l为盾构管片圆弧线长度(mm)；θ为盾构管片圆弧线角度(°)；e1为轴向力作用点至受拉主筋合力点之间的距离(mm)；ei为初始偏心距(mm)；ea为附加偏心距(mm)；ξ1为荷载偏心率对截面曲率的影响系数；ξ2为构件长细比对截面曲率的影响系数。

44、所述大偏心极限承载力的计算公式为：

45、ncu＝α1·fc·b·x+fy'·as'-fy·as

46、

47、其中，α1为混凝土强度调整系数；x为盾构管片混凝土受压区高度(mm)；ncu为盾构管片正截面的极限承载力(kn)。

48、所述小偏心极限承载力的计算公式为：

49、ncu＝α1·fc·b·x+fy'·as'-σs·as

50、

51、

52、

53、其中，σs为小偏心受压时受拉钢筋应力(kpa)；ξ为相对受压区高度(mm)。

54、可选的，所述步骤s5中盾构管片的极限承载力安全系数计算公式为：

55、s＝ncu/γ0γrn

56、其中，s为盾构管片的极限承载力安全系数；ncu为盾构管片正截面的极限承载力(kn)；γ0为结构重要性系数；γr为抗力分项系数；n为轴力(kn)。

57、可选的，所述步骤s6中盾构管片环椭圆度计算公式为：

58、x＝｜x1+x2|

59、y＝｜y1+y2|

60、

61、其中，x1为拱腰左侧水平位移(mm)；x2为拱腰右侧水平位移(mm)；y1为拱顶竖向位移(mm)；y2为拱底竖向位移(mm)；x为盾构管片环水平收敛值(mm)；y为盾构管片竖向收敛值(mm)；rc为盾构管片环半径(mm)；e为盾构管片环的椭圆度。

62、可选的，所述步骤s1中盾构管片结构材料包括盾构管片混凝土材料、盾构管片间环向螺栓与纵向螺栓材料。

63、可选的，所述步骤s1中盾构管片拼装形式包括盾构管片分块数量与盾构管片环间错缝角度。

64、可选的，所述步骤s1中盾构管片结构尺寸包括盾构管片内直径、厚度与宽度。

65、可选的，所述步骤s1中盾构管片所处地层条件包括盾构隧道埋深、地下水位以及各土层物理力学参数。

66、可选的，所述各土层物理力学参数包括土层厚度、重度、内摩擦角、黏聚力与泊松比。

67、有益效果：

68、本发明提出了基于非连续壳-弹簧模型的盾构管片安全评估方法，非连续壳-弹簧模型不仅能模拟盾构管片间的错缝拼装形式，还能反映盾构管片结构螺栓处局部的应力集中现象以及横、纵向结构力学响应，较真实地反映了盾构管片的实际受力情况。

69、非连续壳-弹簧模型具有建模简单、计算效率高、能更好地模拟盾构管片的应力状态等优点，运用非连续壳-弹簧模型可以更全面的反映盾构隧道衬砌盾构管片的力学性态，以准确地计算盾构管片结构在地层中的结构力学响应特征，准确评估地层中盾构管片安全性的问题。