一种基于多维信号分析神经网络的测井数据解释方法

本发明涉及测井数据解释，具体涉及一种基于多维信号分析神经网络的测井数据解释方法。

背景技术：

1、多维信号分析在很多领域都有着广阔的应用前景。例如，测井数据解释就是一种典型的多维信号分析任务。测井数据通常由多条测井曲线组成，包括自然电位测井曲线、伽马测井曲线等等，每个测井曲线记录了井眼的地球物理性质。通过对多条测井曲线进行综合分析，可以预测井眼地质信息，包括岩性、孔隙度等等。随着深度学习的兴起，深度神经网络在多维信号分析领域展示出强大的生命力。然而，现有的方法还存在以下两个主要问题：

2、1、缺少针对多维信号分析的神经网络，已有的网络往往关注不同维度信号的融合，而忽略了信号本身的物理意义，也就是说，需要设计一种网络，不仅能有效地捕捉多个信号维度之间（inter-log）的复杂关系，也能很好地突出单一信号在其维度内（intra-log）的重要特征。

3、2、缺少针对连续信号的迁移学习方法，已有的迁移学习往往关注分类任务（classification），即输出信号是离散的，而对于输出信号取值连续的情况，需要研究回归任务（regression），这在已有研究中尚不充分。

技术实现思路

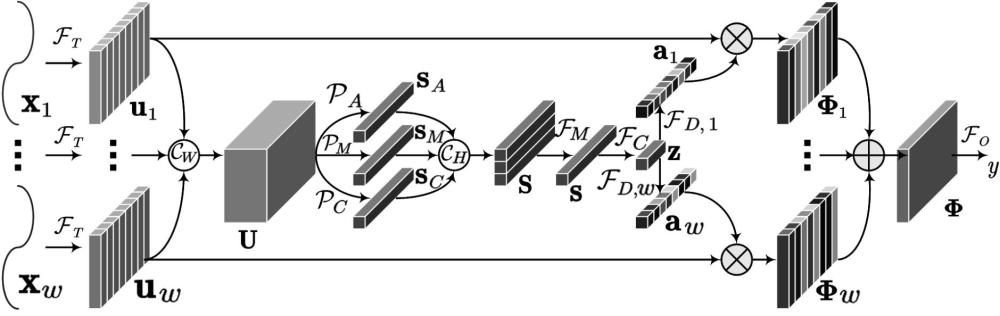
1、为解决上述技术问题，本发明提供一种基于多维信号分析神经网络的测井数据解释方法。神经网络包括单一信号转换、多维信号融合、增强并输出，通过迁移学习方法对该神经网络进行训练，其损失函数包括跨域尺度差异度量函数、跨域角度差异度量函数、奇异值均衡函数和源域监督学习损失函数四个部分。

2、为解决上述技术问题，本发明采用如下技术方案：

3、一种基于多维信号分析神经网络的测井数据解释方法，通过测井数据解释模型对测井数据样本进行解释，得到井的地质信息；具体包括以下步骤：

4、步骤一、单一信号转换：

5、测井数据样本包括同一深度上的多个测井曲线，对测井曲线进行特征变换，得到测井曲线的特征图；表示测井数据样本的第i个测井曲线，表示对应的特征图；h表示测井曲线的视窗长度；表示测井数据样本中测井曲线的数量；表示特征变换模块，c是的特征通道数；表示实数域；

6、步骤二、多维信号融合：

7、将测井曲线的特征图，通过连接操作得到测井曲线的整体特征图；通过全局统计池化获取整体特征图在通道上的统计信息，得到池化结果；将池化结果通过压缩网络得到压缩向量；

8、步骤三、增强并输出：

9、使用扩张网络对变换，获得不同测井曲线的特征图对应的通道注意力，具体表达如下：

10、；

11、将各测井曲线的特征图与对应的通道注意力按通道相乘并相加，得到综合测井曲线特征图：

12、；

13、其中，表示按通道相乘；

14、通过将输入到输出网络，得到井的地质信息。

15、进一步地，步骤一中，所述特征变换模块由一维卷积与relu激活函数组成。

16、进一步地，步骤二中，所述将测井曲线的特征图通过连接操作得到测井曲线的整体特征图，具体包括：

17、；

18、其中，表示按照宽度维度进行连接。

19、进一步地，步骤二中，所述全局统计池化包括全局平均池化、全局最大池化和全局协方差池化；步骤二中，所述通过全局统计池化获取整体特征图在通道上的统计信息，得到池化结果，将池化结果通过压缩网络得到压缩向量，具体包括：

20、全局平均池化通过计算每个通道的平均值来度量整体特征图的中心趋势，得到全局平均池化结果，具体表达如下：

21、；

22、的第k个通道元素为：

23、；

24、表示整体特征图第k个通道特征图，；

25、全局最大池化通过计算每个通道的最大值来度量整体特征图的最显著特征，得到全局最大池化结果，具体表达如下：

26、；

27、的第k个通道元素为：

28、；

29、表示取最大值；

30、全局协方差池化利用协方差矩阵从整体特征图中融合互补信息，得到全局协方差池化结果，具体表达如下：

31、；

32、其中，协方差矩阵，为对进行变形后的整体特征图，中间变量，上标表示转置，分别表示单位阵和全1阵；

33、第k个通道元素为：

34、；

35、表示协方差矩阵中的元素；

36、对进行连接，得到池化连接结果：

37、；

38、其中，表示按照高度维度进行连接；

39、通过融合网络将池化连接结果中三种不同的池化结果进行融合，得到融合后的池化结果：

40、；

41、将池化结果输入至压缩网络，得到压缩向量：

42、；

43、其中，表示relu激活函数，表示批归一化，表示压缩变换矩阵，r表示压缩率。

44、进一步地，所述融合网络由二维卷积与relu激活函数组成。

45、进一步地，所述压缩网络和扩张网络均为全连接网络，且压缩网络和扩张网络组成瓶颈结构。

46、进一步地，所述输出网络是一个全连接网络。

47、进一步地，步骤三中，所述使用扩张网络对变换，获得不同测井曲线的特征图对应的通道注意力，具体包括：

48、不同的测井曲线特征图，通过对应的扩张网络，得到对应的通道注意力：

49、；

50、其中，表示扩张网络对应的扩张变换矩阵；所有的通道注意力之和为全1向量。

51、进一步地，设计损失函数，并对所述测井数据解释模型进行训练，具体包括：

52、对于一个测井数据样本，通过测井数据解释模型能够得到综合测井曲线特征图，将拉平后得到拉平特征，中间变量；对于一批包含b个测井数据样本的训练批，能够得到特征矩阵；表示对应的拉平特征，对特征矩阵的gram矩阵进行特征值分解：

53、；

54、其中，为特征值矩阵，的对角元素为的奇异值的平方，为的右奇异矩阵；上标表示转置，表示对角矩阵，表示特征值矩阵中的第p个特征值，表示右奇异矩阵中的第p个特征性向量；

55、设计跨域尺度差异度量函数：

56、；

57、其中，表示源域的特征矩阵对应的特征值矩阵，表示目标域的特征矩阵对应的特征值矩阵，和分别由源域测井数据样本的训练批和目标域测井数据样本的训练批得到；表示源域第个测井数据样本，表示目标域第个测井数据样本；表示l2范数；

58、设计跨域角度差异度量函数：

59、；

60、其中，表示l1范数，表示角度差向量；

61、；

62、；

63、其中，表示第p’个角度差，表示源域测井数据样本对应的第p’个特征向量；表示目标域测井数据样本对应的第p’个特征向量；

64、分别对源域的特征矩阵和目标域的特征矩阵的最大的e个奇异值进行抑制，得到奇异值均衡函数：

65、；

66、表示源域测井数据样本对应的第e大的特征值，表示目标域测井数据样本对应的第e大的特征值；

67、使用源域的标签信息进行监督学习，源域的监督学习损失为：

68、；

69、其中，和分别是训练批第b个源域测井数据样本的预测结果和标签；

70、收集训练样本，训练样本包括有标签的源域测井数据样本和无标签的目标域测井数据样本；计算综合损失函数：

71、；

72、表示权重参数；通过训练样本和综合损失函数，朝着综合损失函数最小化的方向训练测井数据解释模型，直到综合损失函数收敛或达到训练次数上限。

73、与现有技术相比，本发明的有益技术效果是：

74、（1）本发明设计了一种针对多维信号分析的神经网络，能有效捕获多维信号，即测井数据样本，之间的复杂关系，同时能够突出单一信号内部的重点特征；（2）设计了一种训练神经网络的迁移学习方法，在提升特征学习的可迁移性的同时，能够保持特征对预测目标的敏感性。