一种基于拉格朗日松弛的易碎品物流仓储调度方法及系统

本发明属于物流运输，具体涉及一种基于拉格朗日松弛的易碎品物流仓储调度方法及系统。

背景技术：

1、易碎品仓储是现代物流运输的一个重要组成部分，也是物流运输行业的一大难题。由于其商品的特殊性，易碎品仓储对仓储环节中货箱的稳定性有较高的要求，导致其对仓储环境有着较为严格的限制，单位仓储空间成本较高。因此，易碎品仓储时的空间规划显得尤为重要。优秀的运输空间规划算法可以避免大量的空间浪费，进而减少运输成本，提高经济效益。易碎品由于其商品特殊性，不允许堆叠仓储，因此易碎品仓储问题可以被描述为维度由商品的长宽二维组成的二维装箱问题的变式。

2、装箱问题属于经典的np-hard问题，无法在线性时间内给出问题的最优解。经典的装箱问题描述为，把一批具有多个种类、每种类有多个的物品装入容量相同的箱子内，使得每个箱子中的物品占据的总容量不超过箱子的容量，同时要求装入所有物品消耗的箱子总数最少。

3、对于装箱问题，目前已经存在许多简单易行的求解算法，比较具有代表性的有：

4、first fit：将空闲箱体链以地址递增的顺序连接；在进行容量分配时，从链首开始顺序查找，直到找到一块箱体的大小可以满足需求时，按照该作业的大小，从该箱体中分配出容量，将剩下的空闲箱体仍然链在空闲箱体链中；

5、next fit：分配容量时不是从链首进行查找可以分配容量的空闲箱体，而是从上一次分配容量的空闲箱体的下一个箱体开始查找，直到找到可以为该进程分配容量的空闲箱体；

6、best fit：将空闲箱体链中的空闲箱体按照空闲箱体由小到大的顺序排序，每次从链首进行查找合适的空闲箱体为作业分配容量；

7、random fit与best fit算法相反，将空闲箱体链的箱体按照从大到小的顺序排序形成空闲箱体链，每次查找时检查第一个空闲箱体是否满足；

8、least full first：剩余空间最大且满足所选货物空间需求的箱体优先放置。

9、most full first：剩余空间最小且满足所选货物空间需求的箱体优先放置。

10、此外，还有很多非基于fit的装箱放置算法。具有代表性的有数学规划法、数值优化方法和现代优化方法。数学规划法主要由分枝定界法、动态规划法、整数规划法和线性规划法等方法构成。现代优化方法以遗传算法和模拟退火法为代表。

11、相比于传统装箱问题，易碎品仓储问题产生了新的变式。首先，由于现代物流各分区间货架容量不统一，传统装箱的“箱体容量相同”这一条件不再满足。同时，由于不同容量的货架耗费的仓储空间成本不统一，增加仓储空间导致的成本增加也不能再简单由“箱体数量增加”作为衡量。加之，针对现有的装箱模型的装箱fit算法在仓储需求接近仓库最大容量时，表现出的性能不尽人意。因此，需要对传统的装箱问题模型进行修正，建立更适配实际运行场景应用的装箱模型。

12、近年来，随着物流运输行业需求的变化，仓储空间调度方法也迎来了新的挑战。首先是在调度中，仓储分区数量显著增加，求解规模显著增大，这使得非fit类算法的求解难度显著上升，求解时间也随之增加。其次，由于降低运行成本的需要，调度方法可行解的优度要求也逐渐提高。面对上述问题，现有的方法暴露了显著的弊端。fit类算法能够保证求解速度，但在优度上难以保证，所得的可行解与最优解的间隙较大，而非fit类算法虽然能保证求解优度，但求解时间长，难以满足物流仓储场景大规模、多批次调度需求。因此，为解决易碎品物流仓储调度的实际需求，需要设计新的物流仓储调度方法与系统。

技术实现思路

1、本发明所要解决的技术问题在于针对上述现有技术中的不足，提供一种基于拉格朗日松弛的易碎品物流仓储调度方法及系统，用于解决大规模物流仓储场景下的物流仓储空间快速调度的技术问题，求解时间短，解优度高。)

2、本发明采用以下技术方案：

3、一种基于拉格朗日松弛的易碎品物流仓储调度方法，包括以下步骤：

4、s1、获取易碎品仓储实际运行场景物流调度参数；

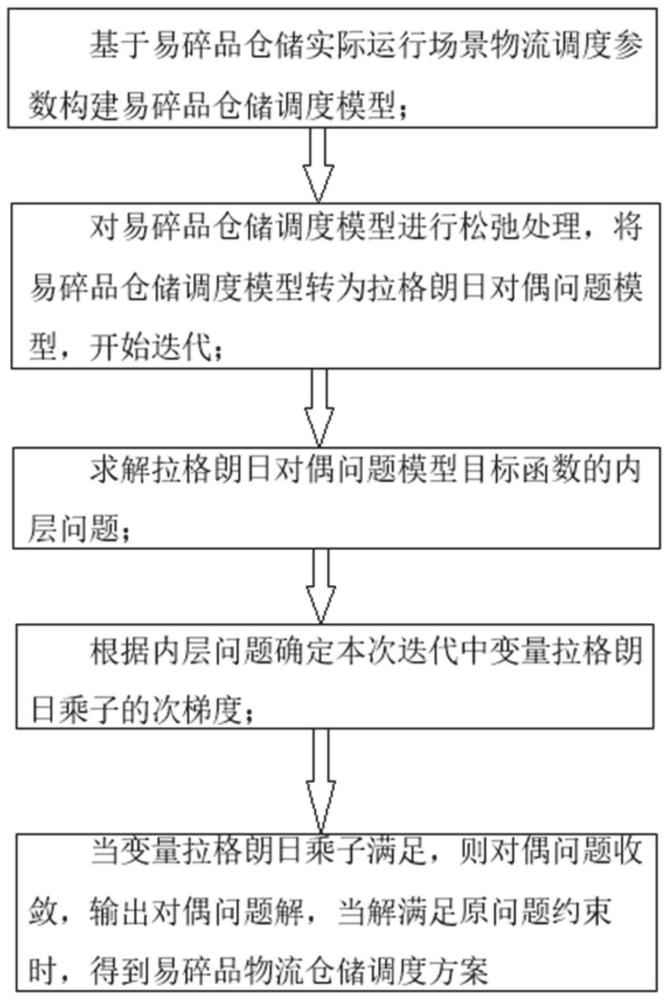
5、s2、基于步骤s1得到的易碎品仓储实际运行场景物流调度参数构建易碎品仓储调度模型；

6、s3、对步骤s2得到的易碎品仓储调度模型进行松弛处理，将易碎品仓储调度模型转为拉格朗日对偶问题模型，开始第x次迭代，x初始值为0；

7、s4、求解步骤s3得到的拉格朗日对偶问题模型目标函数的内层问题；

8、s5、根据步骤s4得到的内层问题确定本次迭代中变量拉格朗日乘子的次梯度；

9、s6、当步骤s5中变量拉格朗日乘子满足λk+1-λk<ε，则对偶问题收敛，继续执行步骤s7；

10、s7、输出对偶问题解，当解满足原问题约束，得到易碎品物流仓储调度方案。

11、优选地，步骤s2中，易碎品仓储调度模型的目标函数如下：

12、

13、其中，φ为仓储方案产生的总收益，ωi为存储规格为i的包装所能产生的收益，xik为第k个仓储分区上放置规格为i的包装的数量，k为仓储分区的总数，n为包装规格类型总数。

14、更优选地，易碎品仓储调度模型的约束条件包括：

15、需求约束

16、

17、其中，i＝1,2,...,n，ni为用户对规格类型为i的包装的需求量；

18、容量约束

19、

20、其中，k＝1,2,...,k，γ＝1,2,...,υ，ai(γ)为规格类型为i的尺寸参数，rk(γ)为第k个分区可供仓储的空间，υ为尺寸类型；

21、非负整数约束：

22、xik∈ν

23、其中，xik为第k个仓储分区上放置规格为i的包装的数量。

24、优选地，步骤s3中，拉格朗日对偶问题模型的的目标函数包括：

25、内层问题

26、

27、其中，λi为第i项拉格朗日乘子，i＝1,2,...,n，ωi为存储规格为i的包装所能产生的收益，xik为第k个仓储分区上放置规格为i的包装的数量，ni为用户对规格类型为i的包装的需求量；

28、外层问题

29、

30、拉格朗日对偶问题模型的一组次梯度为：

31、

32、优选地，步骤s4中，拉格朗日对偶问题模型目标函数的内层问题具体为：

33、s401、初始化生成一张横坐标为l，纵坐标为h的初始表，表的横坐标为仓库的最大分区长度，纵坐标为最大分区宽度。

34、s402、从占据空间最少的货物类型出发，设其占据的资源为xlyh，x为包装规格类型长度，y为包装规格类型宽度，对表内的每一点(i,j)，取χij；

35、s403、当未迭代的货物类型数量为0，则输出完全背包问题最优解表，不为0则选择下一个迭代的货物类型，继续执行步骤s402。

36、更优选地，步骤s402中，χij为：

37、χij＝max{χij,χ(i-xl)(j-ym)+vxlym}

38、其中，χ(i-xl)(j-ym)为装入一个当前迭代的货物后的剩余空间的最大收益，vxlym为装入一个当前迭代的货物所对应的收益。

39、优选地，步骤s5中，根据次梯度下降法更新拉格朗日乘子λ，迭代公式为：

40、

41、其中，ρk为步长系数，为本次迭代的解带入原问题所得到的一个目标函数值，ul为原问题的一个下界。

42、更优选地，衡量本次迭代性能的参数ρk的取值为：

43、

44、其中，(uk-uk-1)为当前迭代对偶目标减去前次迭代对偶目标的差值。

45、优选地，当对偶问题解不满足原问题约束，将对偶解还原可行解，得到原问题的可行解，得到易碎品物流仓储调度方案，具体如下：

46、s901、将对偶解中为未来预留的空间视为新的分区，依剩余空间升序排序形成新分区链；

47、s902、对未满足需求数量的货物规格类型，依使用空间量降序排列成新需求队列；

48、s903、对新需求队列中每个货物规格类型，从新分区链首开始遍历，直到找到第一个能够放下1个该类型的货物的节点，放入1个货物，重复上述操作，直到所有货物规格类型的货物数量都满足需求。

49、s904、对于还原可行解中未执行过分区化的货物，采用原对偶解放置方案，对于分区化后的货物，生成的新分区中的剩余空间，依剩余空间查询步骤s4生成的完全背包问题最优解表生成余量放置方案，与步骤s903放下的未分区化货物组合，形成最终的放置方案。

50、第二方面，本发明实施例提供了一种基于拉格朗日松弛的易碎品物流仓储调度系统，其特征在于，包括：

51、构建模块，基于易碎品仓储实际运行场景物流调度参数构建易碎品仓储调度模型；

52、迭代模块，对构建模块得到的易碎品仓储调度模型进行松弛处理，将易碎品仓储调度模型转为拉格朗日对偶问题模型，开始第x次迭代，x初始值为0；

53、求解模块，求解迭代模块得到的拉格朗日对偶问题模型目标函数的内层问题，根据内层问题确定本次迭代中变量拉格朗日乘子的次梯度；

54、输出模块，当求解模块中变量拉格朗日乘子满足λk+1-λk<ε，则对偶问题收敛，输出对偶问题解，当解满足原问题约束，得到易碎品物流仓储调度方案。

55、第三方面，一种芯片，包括存储器、处理器以及存储在所述存储器中并可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述基于拉格朗日松弛的易碎品物流仓储调度方法的步骤。

56、第四方面，本发明实施例提供了一种电子设备，包括计算机程序，所述计算机程序被电子设备执行时实现上述基于拉格朗日松弛的易碎品物流仓储调度方法的步骤。

57、与现有技术相比，本发明至少具有以下有益效果：

58、一种基于拉格朗日松弛的易碎品物流仓储调度方法，在拉格朗日松弛框架下，建立原求解模型的拉格朗日对偶问题模型，能够得到原问题的一个质量较好的下界，并最终还原为原问题的一个高质量解；在工程应用中，技术人员可以根据实际仓库的分区种类、各分区规模以及易碎品对象的种类和规模，采用本发明提供的算法快速生成单一批次易碎品调度方案，实现仓储调度成本和运营成本的最大化降低，提升经济效益。

59、进一步的，装箱模型变式解决了原装箱模型目标不能正确表达模型求解需求的问题，修正目标函数后的变式模型能够兼容箱体容量不一的场景；具体的，对于容量不一、耗费成本不同的箱体，变式模型的目标为各箱体依放置方案获得的收益的加和，该目标可以更精确地反映箱体间差异，对于非fit算法而言，采用变式模型可以得到更精确、质量更高的解。

60、进一步的，松弛后的拉格朗日对偶模型具有可拆分的结构特征，进而，本方法可以在求解过程中将一个k个箱体组成的大规模求解问题拆分为k个单箱体小规模完全背包问题求解，显著降低了问题的求解规模；

61、进一步的，将子问题的求解过程转化为了查表过程，基于动态规划法生成拉格朗日对偶问题子问题最优解表，进而，将箱体规模扩大导致的算法求解规模的增加转换成了常数级时间复杂度的规模增加，显著降低了求解规模，进一步增加了本方法的效率和应用时的可扩展性；

62、进一步的，步长迭代方法加入了无理数项，考虑了对偶问题最优解落在无理数域内的可能性，扩大了解空间的搜索范围，提高了解的质量。同时，该方法通过对偶间隙调整步长，相对于传统的定步长搜索法，大大加快了解的收敛速度；

63、进一步的，采用best fit算法还原可行解，在保留了对偶解优度高的性质的同时，采用了启发式方法，保证了求解速度，提高了仓储调度效率。

64、可以理解的是，上述第二方面的有益效果可以参见上述第一方面中的相关描述，在此不再赘述。

65、综上所述，本发明涉及面向物流运输行业的大规模易碎品物流仓储调度问题，可以有效提高易碎品运输批次仓储调度的经济性和效率，为实际物流运输过程中的仓储调度过程的优化规划提供切实有效的调度方案。

66、下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。