一种海上风电场导纳模型聚合方法与流程

本发明属于海上风电场聚合导纳模型，尤其是涉及一种海上风电场导纳模型聚合方法。

背景技术：

1、通常情况下，一个海上风电场内可具有数十台，甚至是数百台风电机组，造成风电场详细模型阶数高。在海上风电场并网系统稳定性检验中，若对海上风电场采用详细模型，通常需耗费大量计算时间，一方面对计算资源和人力需求较高，也就是成本较高；另一方面耗时多，就只能进行简化计算，影响分析结果准确性，因此，需发明一种用于小干扰稳定性检验的风电场小信号模型聚合或降阶方法。

2、当前风电场动态等值的常用方法有容量加权平均法和参数辨识法两种。其中容量加权平均法以一台扩容风电机组代表一个风电场，应用简单，但是用于风电并网系统小干扰稳定性分析时，准确度一般较低。参数辨识法可在一定程度上提高风电场动态等值模型的准确度。等值模型参数的辨识，本质上可看作对一优化问题的求解，其目标函数为相同工况或相同外部扰动作用下等值风电机组和被等值风电场在并网点动态响应的误差最小，待求量为等值风电机组参数。在风电场规划阶段，尚未有风电场并网运行的动态响应数据，若要基于参数辨识法建立风电场动态等值模型，仍需基于全阶模型，通过仿真获取风电场动态响应数据。而且，参数辨识过程涉及非线性优化问题的求解，通常需采用智能优化算法，如粒子群算法和遗传算法等，由此也造成了等值模型参数和被等值风电场内风电机组参数、数量和网络结构之间的关系湮没在对优化问题进行迭代求解的过程中。当风电场内风电机组型号、数量和网络结构发生变化时，均需重新对等值模型参数进行求解。因此，参数辨识法不适用于风电场规划阶段，对不同设计方案进行比选时建立风电场等值模型。因此，有必要针对海上风电项目规划阶段小干扰稳定性检验，提出一种风电场模型聚合或降阶方法。

3、现有类似方法和实现方案主要可分为如下三类：

4、1)基于广义短路比的风电场等值方法。此类研究中，将风电场看作一个自治系统，推导了其小信号模型的等效解耦，其中未考虑风电场的输入输出特性，因此所提方法和所得风电场降阶模型适用于风电场内部稳定性分析。

5、2)现有考虑风电场动态输入输出特性，推导风电场小信号模型等效解耦的研究中，多是以线性化状态空间模型为基础，此类方法仅适用于风电机组详细模型和参数已知的情况，且其中所提风电场单机等值模型仅适用于时域分析。同时，此类研究中大多未考虑风电场线路动态，不适用于对风电场阻抗(导纳)模型的聚合或降阶。而阻抗或导纳模型可在风电机组详细模型和参数未知的条件下，基于测量建立，更具适用价值。

6、3)现有风电场阻抗或导纳模型聚合方法中，多是忽略风电场内部集电网络的影响，将所有风电机组看作对称连接至汇流母线，从而风电场阻抗(导纳)模型可看作所有风电机组阻抗(导纳)模型的并联，实现对风电场阻抗(导纳)模型的聚合。由于未考虑集电网络的影响，此类研究中所提方法无法反映风电场网络结构变化对并网风电场小干扰稳定性的影响。

技术实现思路

1、有鉴于此，本发明旨在提出基于海上风电场详细小信号导纳模型，推导风电场单机等值模型的一般表示形式，可直接根据海上风电场内风电机组型号、数量和网络结构，通过简单计算，建立风电场聚合导纳模型。所建立聚合模型与1台风电机组模型同阶，且可有效反映原风电场的导纳频率特性。

2、为达到上述目的，本发明的技术方案是这样实现的：一种海上风电场导纳模型聚合方法，包括以下步骤：

3、选择风电场内某一台风电机组为代表，建立其小信号模型；

4、根据风电场网络结构和参数建立风电场网络电抗矩阵，并计算其特征值与特征向量；

5、计算海上风电场聚合导纳模型，得到风电场聚合导纳模型。

6、进一步的，假设海上风电场内共n台风电机组，其中风电机组k的小信号模型为，

7、δik＝gk(s)δvk；k＝1,2,...,n   (1)

8、式中，δ表示变量或变量列向量的微小增量；vk＝[vky vky]t，ik＝[ikx iky]t；vkx+jvky和ikx+jiky分别为交流电网公共x-y坐标系下风电机组k的端电压和输出电流；gk(s)为风电机组k的小信号传递函数模型或导纳模型；

9、以海上升压站高压侧母线为参考节点，采用节点阻抗矩阵的形式，海上风电场部分的网络方程为，

10、δv＝zwδi+δvbm    (2)

11、式中，i＝[i1t i2t ... int]t∈r2n×1为风电机组输出电流列向量；v＝[v1t v2t ...vnt]t∈r2n×1为风电机组端电压列向量；vbm＝[vbt vbt ... vbt]t∈r2n×1，vb＝[vbx vby]t，且vbx+jvby为交流电网公共x-y坐标系下海上升压站高压侧母线的电压；zw为海上风电场部分的节点阻抗矩阵，且其通常写为如下形式，

12、

13、由式(1)，得

14、δi＝diag[gk(s)]δv      (3)

15、式中，diag[gk(s)]表示对角线元素为gk(s)的分块对角矩阵，其中，k＝1,2,...,n；

16、将式(2)代入式(3)，消去中间变量δv，可得，

17、δi＝(e2n-diag[gk(s)]zw)-1diag[gk(s)]δvbm    (4.a)

18、令表示海上风电场输出电流，由式(4.a)可得海上风电场导纳模型为，

19、δic＝gw_full(s)δvb     (4.b)

20、式中，ic＝[icx icy]t；

21、若则mij(s)均为2×2的矩阵，i＝1,2,...,n，j＝1,2,...,n；e2n为2n×2n的单位矩阵。

22、进一步的，假设线路电阻可以忽略，则式(2)所示海上风电场部分的网络方程为如下形式，

23、δv＝xwδi+δvbm   (5)

24、式中，假设不考虑线路动态，则表示克罗内克乘积。

25、进一步的，式(5)中矩阵xm的建立原则推导如下：

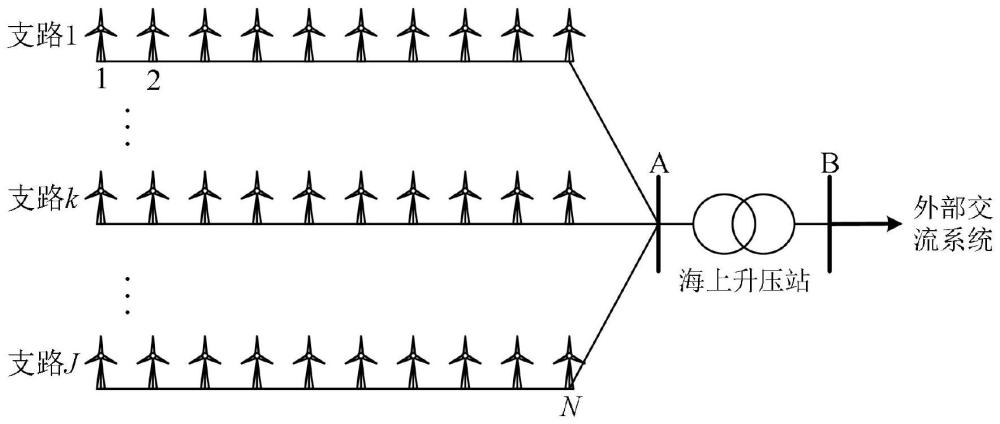
26、海上风电场内共j条支路，j为任意正整数，且所有风电机组按照从支路1到支路j，从左向右递增的顺序编号，且在第j条支路上有nj台风电机组，因此，支路j上风电机组编号范围为至对于支路j上编号为k的风电机组，与其相连的线路电抗为xk，其中流经xk的线路电流ilkx+jilky为风电机组至风电机组k的输出电流之和，即则xk上的电压方程为，

27、δvk＝xke1δilk+δvk+1     (6)

28、当即风电机组k为支路j上最靠近海上风电场汇流母线的风电机组时，

29、

30、式中，vax+jvay为交流电网公共x-y坐标系下海上风电场汇流母线的电压；xl为海上升压站变压器等效电抗；

31、由式(6)和式(7)，

32、

33、式(8)可整理为，

34、

35、由式(9)得，

36、

37、式中，

38、

39、

40、

41、由式(10)，式(5)中矩阵xm中元素xki,i＝1,2,...,n的值根据如下原则计算：

42、若风电机组i不属于支路j，则xki＝xl；

43、若风电机组i在支路j上，且i≤k，则xki为连接风电机组k到海上升压站高压侧母线的线路电抗之和；

44、若风电机组i在支路j上，且i＞k，则xki为连接风电机组i到海上升压站高压侧母线的线路电抗之和。

45、进一步的，根据xm的推导与说明，矩阵xm为一实对称矩阵，且其中的元素均为正实数，若矩阵xm的特征值为ρi，对应的特征向量为ti，其中i＝1,2,...,n，则有如下对角化变换成立，

46、

47、式中，diag[ρi]表示对角线元素为ρi,i＝1,2,...,n的对角矩阵，tn＝[t1 t2 ...tn]为特征向量ti构成的矩阵，且tn∈rn×n；

48、参照式(11)所示相似对角化变换，对海上风电场小信号模型引入如下变量变换，

49、δv＝t2δvy δi＝t2δiy     (12)

50、式中，e2为2×2的单位矩阵；

51、根据克罗内克乘积的性质，有：将式(12)所示变量变换代入式(2)并推导可得，

52、t2δvy＝zwt2δiy+δvbm   (13)

53、对式(13)左右两边同乘t2t可得，

54、δvy＝t2tzwt2δiy+t2tδvbm   (14)

55、式中，

56、结合式(11)，若忽略网络电阻，则根据克罗内克乘积的性质，

57、

58、若海上风电场内风电机组的小信号模型相同，其传递函数矩阵均为gw(s)，则将式(12)代入式(3)可得，

59、t2δiy＝diag[gw(s)]t2δvy   (16)

60、对式(16)左右两边同乘t2t可得，

61、δiy＝t2tdiag[gw(s)]t2δvy   (17)

62、根据克罗内克乘积的性质，t2tdiag[gw(s)]t2＝diag[gw(s)]，因此，式(17)可简化为，

63、δiy＝diag[gw(s)]δvy   (18)

64、结合式(12)，海上风电场输出电流为，

65、

66、由式(14)、式(15)、式(18)和式(19)可知，当采用变量δiy和δvy描述海上风电场动态特性时，原风电场小信号模型解耦为n个相互独立的等效子系统，其中，第i个等效子系统的小信号模型为，

67、

68、式中，δici＝[δicix δiciy]t，icix+jiciy为公共x-y坐标系下，等效子系统i的输出电流；

69、式(20.a)也可以写为如下形式，

70、δici＝gesi(s)δvb      (20.b)

71、式中，gesi(s)＝ti2[e2-ρigw(s)e1]-1gw(s)，为第i个等效子系统的导纳模型。

72、进一步的，根据给出的矩阵xm的形成原则，矩阵xm可进一步写为如下形式，

73、xm＝xnet+xl     (21)

74、式中，

75、式(21)中，矩阵xnet与海上风电场集电网络部分对应，矩阵xl与海上升压站变压器等效电抗对应，集电线路用于功率汇集，通常情况下，相对于海上升压站变压器电抗而言，集电线路电抗很小，而且，根据节点阻抗矩阵的性质，式(21)中矩阵xnet一般为一个稀疏矩阵，尤其是在海上风电场内，风电机组输出功率通过多条出线汇集至汇流母线时，矩阵xnet的稀疏性愈发明显，因此，矩阵xm可看作由矩阵xl主导，若矩阵xl的特征值为ρli，对应的特征向量为tli，其中i＝1,2,...,n，则有如下关系成立，

76、ρli＝0,i＝1,2,...,n-1ρln＝nxl     (22)

77、

78、式中，tlki为列向量tli中的第k个元素；

79、因此，对于矩阵xm的特征值和特征向量近似有如下关系成立，

80、ρn＞＞ρi tn＞＞ti；i＝1,2,...,n-1    (24)

81、由式(19)、式(20)和式(24)，海上风电场整体的动态输出特性集中体现在第n个等效子系统中，即风电场并网运行的主导振荡模式通常体现在第n个等效子系统中，可以根据第n个等效子系统建立风电场单机等值模型，得到海上风电场聚合导纳模型如下，

82、δic≈δicn＝gw_offshore(s)δvb      (25)

83、式中，gw_offshore(s)＝tn2[e2-ρngw(s)e1]-1gw(s)，为海上风电场聚合导纳模型。

84、进一步的，式(25)所示风电场聚合导纳模型是在海上风电场内所有风电机组小信号模型相同的条件下推导得到的,对于这一条件在实际情况下的可成立性作进一步说明如下：

85、实际中一个风电场内通常采用来自同一厂家且同一型号的风电机组，各风电机组初始参数设定相同；若风电场内风速空间分布无显著差异，则各风电机组导纳模型近似相同，在推导风电场聚合模型时，可假设各风电机组导纳模型相同；尤其是在风电场规划阶段，可对所选型号的风电机组采用典型模型，参数和运行状态，此时，各风电机组小信号模型基本完全一致；

86、对于一些大规模风电场，其中可能具有几种不同型号的风电机组，或风电机组稳态运行点可能具有显著分散性，此时，可根据风电机组型号和运行点的相似程度，将风电场划分为若干由型号相同且工况相似的风电机组构成的风电机群，再建立各风电机群的聚合导纳模型。

87、进一步的，根据建立的风电场聚合导纳模型与外部交流系统阻抗模型相乘所获得矩阵特征值的奈奎斯特曲线判定海上风电场并网系统小干扰稳定性。

88、相对于现有技术，本发明所述的海上风电场导纳模型聚合方法具有以下优势：本发明中，基于海上风电场详细小信号导纳模型，推导了风电场单机等值模型的一般表示形式，可直接根据海上风电场内风电机组型号、数量和网络结构，通过简单计算，建立风电场聚合导纳模型。所建立聚合模型与1台风电机组模型同阶，且可有效反映原风电场的导纳频率特性。

89、(1)本发明在考虑风电场输入输出特性的条件下，推导了风电场导纳模型的等效解耦，实现了将n机风电场导纳模型解耦为n个相互独立的等效子系统，且各等效子系统可看作由一台风电机组并网构成；

90、(2)本发明基于所述等效解耦方法，进一步建立了风电场聚合导纳模型，实现了将n机风电场导纳模型，聚合为由1台风电机组并网构成系统的导纳模型。