基于主动学习策略和自构造神经网络的半监督软测量方法

本发明属于人工智能，涉及一种基于主动学习策略和自构造神经网络的半监督软测量方法。

背景技术：

1、数据驱动的建模方法依赖于大量的数据，然而在实际工业过程中，由于标记成本昂贵、采样率低、工业现场环境恶劣等因素，数据的获取非常困难。传统软测量建模的方法大多数只利用有标签样本，而大量蕴含在无标签样本中的有用信息都会被忽略，当有标签样本有限时，提供的先验信息也有限。监督式的建模方法无法保证数据驱动模型的预测性能。

2、本发明设计了一种基于主动学习策略和自构造神经网络的半监督软测量方法，将半监督学习和工业过程软测量建模结合起来，为了对有标签样本进行数据增强，通过主动学习从大量无标签样本中选取最有价值、对模型提升最大的无标签样本，不仅能实现关键质量变量的实时预测估计，同时又能最大程度的提高软测量模型的性能。

技术实现思路

1、发明目的：针对背景技术中指出的问题，本发明提出一种基于主动学习策略和自构造神经网络的半监督软测量方法，通过引入对输入空间划分更为灵活的非对称高斯函数作为隶属函数，对sofnn-hps结构调整、主动学习挑选样本，对出水氨氮数据进行预测，此方法不仅有助于提高模型的计算效率，而且有利于提高模型的分类精度。

2、技术方案：本发明提供了一种基于主动学习策略和自构造神经网络的半监督软测量方法，包括如下步骤：

3、步骤1：利用传感器阵列对污水的水温wt、ph、溶解氧do、高锰酸钾kmno4、总磷tp、总氮tn、电导率ec、浊度tu、叶绿素chl、藻密度acd共10个易测变量进行检测，利用水杨酸分光度法测定对应的氨氮nh3-n含量，生成一批样本输入输出对作为数据集，将该数据集分为有标签数据集和无标签数据集；

4、步骤2：构建sofnn-hps模型，具有四层结构，分别为输入层、隶属函数层、规则层和输出层，引入非对称高斯函数作为隶属函数，增强非线性系统模糊规则的表征能力；

5、步骤3：所述sofnn-hps模型的结构辨识包含三个部分：模糊规则的增长和修剪以及隶属函数和模糊规则的合并，设计模糊规则分层修剪策略，利用其删除冗余模糊规则，同时利用几何增长准则自动生成模糊规则并采用自适应分配策略来设置模糊规则的前件参数；

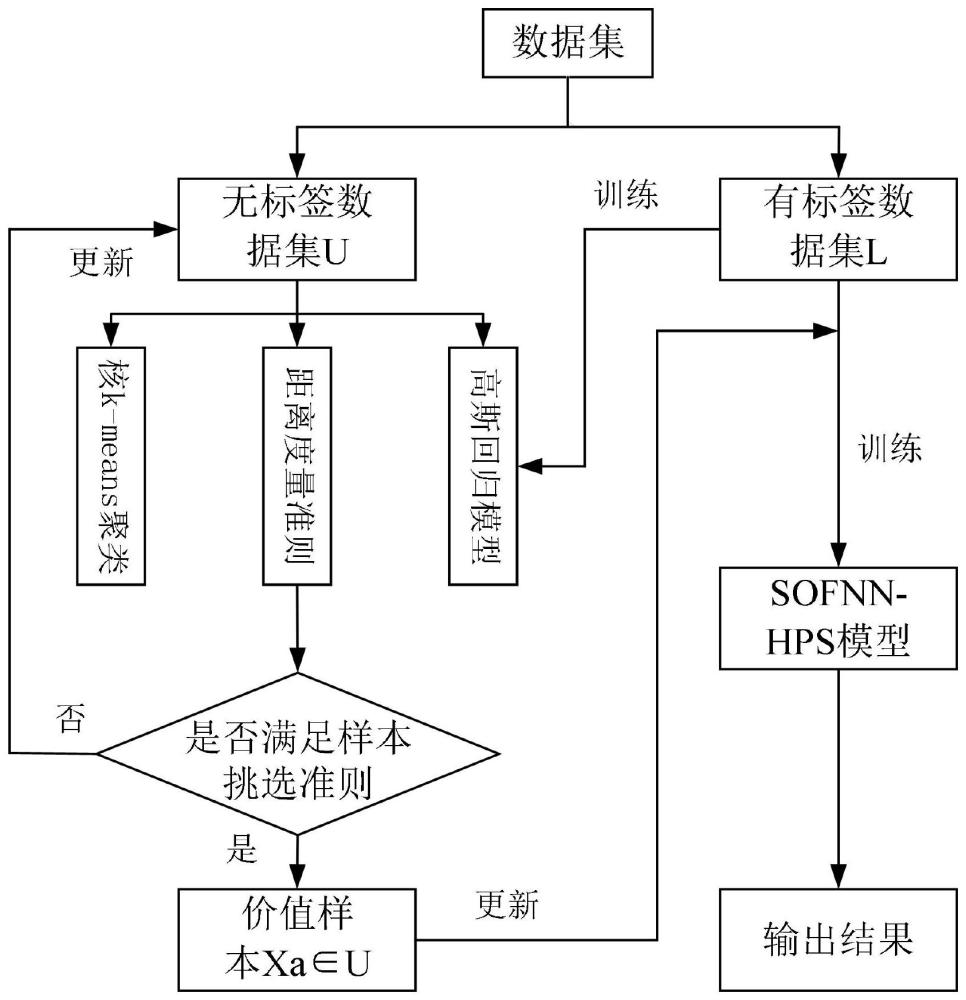
6、步骤4：在主动学习中采用核k-means算法、距离度量准则以及高斯回归模型对无标签数据进行选择，得到价值量较大的样本，将其加入到有标签数据集中，对有标签数据集进行数据增强更新；

7、步骤5：用sofnn-hps模型对已更新有标签数据集进行训练，预测出水氨氮浓度。

8、进一步地，所述步骤2的具体步骤如下：

9、sofnn-hps模型采用非对称高斯函数agf作为隶属函数，gd-fnn中的椭球基函数ebf被扩展为广义椭球基功能gebf；

10、所述sofnn-hps模型等价于一个由以下模糊规则描述的t-s模糊推理系统：

11、t-s模糊神经网络fnn的模糊规则描述如下：

12、rj：ifx1 isa1j,...,xn isanj,theny isf(x1,…,xn)

13、式中，j＝1,2，…，r，r表示模糊规则个数，f(x1，…，xn)是输入变量xi的线性函数；

14、输入层：每个节点与输入量x＝[x1,x2,…,xn]t相连接，n为输入变量个数，即节点个数；

15、隶属函数层：该层中的每个神经元表示执行模糊化操作的隶属函数，使用具有动态宽度的agf，xi的第j个agf模糊集神经元的输出由下式给出：

16、

17、

18、其中，cij、σijl和σijr分别为第j条模糊规则的第i个隶属函数的中心、左宽度和右宽度，当xi位于cij的左侧或右侧时，xi的隶属函数值μij(xi)取值并不一样；

19、规则层：每个神经元代表一个潜在模糊规则中的if部分，即前件参数，因此规则层的神经元数等于模糊规则数：

20、

21、其中，x＝[x1,x2,…,xr]t,cj＝[c1j,c2j,…,crj]t,和σj(x)＝[σ1j(x1),σ2j(x2),…,σrj(xr)]t分别代表输入向量、第j个gebf的中心向量和动态宽度向量；

22、输出层：对于一个多输入单输出系统而言，该层仅有一个神经元代表系统的输出变量，该层的输出使用解模糊运算计算获得，该运算是输入信号的加权和，可以表示为：

23、

24、其中，wj为第j条模糊规则的then部分，即后件参数，对于t-s模型，wj为输入变量的多项式，如下：

25、wj＝a0j+a1jx1+…+arjxr,j＝1,2,…,u,

26、其中，a0j,a1j,…,arj(j＝1,2…,u)为第j条规则中输入变量的权值，每个模糊规则有1+r个后件权值。

27、进一步地，所述步骤3中sofnn-hps模型的结模糊规则的增长如下：

28、对于模糊规则数的增长，引入下述两个判据：

29、(1)系统误差判据

30、对于第k个观测数据(xk，tk)，其中，tk是期望的输出，yk是实际的输出，定义系统误差为：

31、||εk||＝||tk-yk||

32、(2)可容纳边界

33、如果一个新样本位于某个存在的高斯函数的覆盖范围即可容纳边界内，样本就可以用已经存在的高斯函数代表，则无须产生新的高斯函数；

34、对第k个观测数据(xk，tk)计算输入值xk和现有的高斯函数单元的中心cj之间的距离dk(j)，即：

35、dk(j)＝||xi-cj||j＝1,2,...u

36、令dmin＝min(dk(j))，如果dmin＞kd，则要考虑增加一条模糊规则，否则该输入数据由现有的最近的高斯函数表示，kd为可容纳边界的有效变量；

37、当进行模型的离线训练时，对ke和kd进行动态调节：首先设置比较大的ke和kd，确定产生输出误差大而没有被现有模糊规则覆盖的位置，通过网络的训练，不断缩小ke和kd：

38、ke＝max[emax×βi,emin]

39、kd＝max[dmax×γi,dmin]

40、式中：εmax为预先定义好的最大误差；εmin为期望的dfnn精度；β为收敛常数，0＜β＜1；dmax为输入空间的最大长度；dmin为最小长度；γ为衰减常数，0＜γ＜1；

41、基于上述两个指标，考虑以下4种情况：

42、a)当||εk||≤ke，dmin≤kd时，表明sofnn-hps可以完全适应观测结果(xk，tk)，不需要增加模糊规则；

43、b)当||εk||≤ke，dmin＞kd时，表明sofnn-hps这说明该系统具有良好的泛化性，只需要调整权重；

44、c)当||εk||＞ke，dmin＞kd时，表明当前sofnn-hps的泛化性能不好且有规则无法覆盖当前样本时，需要增加一条模糊规则；

45、d)当||εk||＞ke，dmin≤kd时，表明尽管xk可以聚集在已有的高斯函数附近，但覆盖xk的高斯函数泛化能力并不是很好，不需要增加模糊规则，但高斯函数的中心和宽度需要被更新；

46、当第一个观测数据(x1,t1)进入系统后，形成如下第一条模糊规则：

47、

48、其中，ci1、σi1l和σi1r分别是xi的第一个模糊规则的中心、左宽度和右宽度，σ0是预设的宽度常数；

49、当一条新的模糊规则产生后，利用隶属函数的相似性来决定是否给多维输入变量xk的第i维数据xik分配一个新的agf，令xik对应的中心向量为φi＝[ci1,ci2,…,ciu]t，则xik与φi之间的欧氏距离为：

50、

51、此外，通过计算最小欧氏距离，找到最接近xik的agf，如下：

52、

53、如果edi(jn)≤km，则xik可以完全由最近的agf表示，并且新生成的规则不需要在第i个输入维度中生成新的agf；此时，此新规则的第i个模糊集的参数(即中心和动态宽度)设置为与agfjn相同的值，从而使规则库更加透明；

54、

55、其中，ci,u+1、σi,u+1l和σi,u+1r分别是xik样本下新规则的中心、左宽度和右宽度；

56、如果edi(jn)>km，则需要给xik分配一个新的agf，则新生成的u+1条模糊规则的前件参数初始化为：

57、

58、其中，ci,u+1、σi,u+1l和σi,u+1r分别是xik样本下新规则的中心、左宽度和右宽度，ko是重叠因子，ko>1。

59、进一步地，所述步骤3中sofnn-hps模型的规则修剪具体如下：

60、先利用模糊规则密度指标识别出不重要的规则或规则集，再利用误差下降率法剔除最不重要的规则，当第k个样本(xk,tk)到来时，计算gebf神经元的激活强度为：

61、

62、其中，xk＝[x1k,x2k,…,xrk]t为第k个样本的输入向量；

63、然后，计算gebf神经元的激活强度的最大值为：

64、

65、其中，j*表示具有最大激活强度的gebf神经元的索引；模糊规则j*为现有规则库中最重要的规则，其密度更新如下：

66、

67、其中，和分别是规则j*在k-1和k时的密度，对于新产生的模糊规则，其初始密度设置为1；经过δk次迭代后，δk称为修剪周期，辨识出密度值小于预设阈值的规则：

68、jδ＝{j|denj(k)＜dth,1≤j≤u},

69、其中，jδ表示一组不活跃规则，dth为预设的密度阈值，如果jδ中仅有一条模糊规则，则删除该不重要的规则；如果jδ中有多条模糊规则，则基于误差下降率法err计算表征它们的重要性的值，并删除具有最小值的规则，第j条模糊规则被修剪，则其参数设置如下：

70、

71、并且模糊规则数r＝r-1。

72、进一步地，所述步骤3中sofnn-hps模型的隶属函数和模糊规则的合并具体如下：

73、在模糊规则分配前提参数时，会生成具有相同中心的隶属函数，对具有相同中心的隶属函数进行合并操作；对于输入变量xi，假设其有m个隶属函数具有相同的中心cis、不同的左宽度[σi,s1l,σi,s2l,…,σi,snl]和右宽度[σi,s1r,σi,s2r,…,σi,snr]，则新的隶属函数的中心和动态宽度可以通过合并m个agfs获得：

74、ci,new＝ci,s,

75、

76、

77、其中，ci,new、σi,newl和σi,newr分别是执行隶属函数合并操作后的xi的新agf神经元的中心、左宽度和右宽度；这种组合操作在一次执行中只处理输入向量的第i维，将从网络拓扑中删除具有相同中心的m个agf神经元；

78、在执行隶属函数合并操作后，如果模糊规则具有相同的前提参数，将这些相同的模糊规则合并成一个单独的规则，假设规则j和规则j′相同，则新的规则以及规则j和j′的参数定义为：

79、

80、

81、其中，ci,new、σi,newl和σi,newr分别是对规则执行合并操作后的xi的新gebf神经元的中心、左宽度和右宽度。

82、进一步地，所述步骤4中在主动学习中采用核k-means算法、距离度量准则以及高斯回归模型对样本进行选择，得到价值量较大的样本具体操作如下：

83、(1)核k-means算法，将无标签数据集和有标签数据集里面的数据各分成20个聚类，将t个未标记样本映射到高维核空间为再划分为k个簇，首先在高维和空间中的任意样本xi和xj的距离d(xi,xj)为：

84、d2＝(xi,xj)＝||φ(xi)-φ(xj)||2

85、  ＝φ2(xi)-2φ(xi)φ(xj)-φ2(xj)

86、  ＝k(xi·xi)-2k(xi·xj)+k(xj·xj)

87、其中，φ(xi)和φ(xj)分别为样本xi和xj在高维空间中的映射，高维核空间中的簇中心uk为：

88、

89、其中，|ck|为簇ck中的样本数量，且|ck|的数学表达式为：

90、

91、其中，sign()为指示函数具体为：

92、

93、而sign(φ(xi),ck)为高维和空间上的指示函数，样本xi在高维核空间中的映射φ(xi)与簇中心uk的距离为：

94、

95、其中，f(xi,ck)和g(ck)分别为：

96、

97、

98、则上式可以写为：

99、

100、上式中的k(xi,xi)可以被省略因为(xi,xi)对于确定最近的簇没有帮助，对于每一个簇ck，通过下式选择距离中心最近的样本作为该簇类的代表：

101、

102、(2)距离度量准则，将无标签数据集和有标签数据集中的聚类进行距离度量计算，因为有标签样本和无标签样本都含有输入信息，而无标签样本没有标签信息，因此只考虑有标签样本和无标签样本的输入信息，基于欧式距离的度量准则为：

103、

104、其中，dl,p,el表示有标签样本集中第l个聚类和无标签样本集中第p个聚类之间的欧式距离，n表示输入变量的维度，xl,i表示有标签样本集第l个聚类的第i维输入变量，xp,j表示有标签样本集第p个聚类的第j维输入变量，通过选取与所有有标签聚类距离和最大的若干无标签聚类，选择出最有价值的无标签聚类；

105、得到一个无标签聚类和一个有标签聚类之间的距离，把该无标签聚类与所有有标签聚类的距离做累加，得到该无标签聚类和有标签聚类的差异性，最后映射得出无标签的样本数据：

106、

107、其中，dp表示无标签样本集中第p个聚类和有标签聚类的差异性，n表示有标签样本的数目，差异性越大，表示该无标签聚类与有标签聚类中的样本信息越不同，从而选择出来进行标注，然后更新有标签样本数据集，不断迭代，直到满足停止条件为止；

108、(3)高斯回归模型gpr，在采用距离度量准则的主动学习中，计算所有未标注聚类的dp，从大到小排序，选择其中最大值对应的聚类交由专家进行标注后放入训练集中进行训练，将预测方差作为评估回归性能的重要指标，建立高斯过程回归模型得到样本的预测方差作为样本信息度的评估准则，运用gpr模型对已挑选聚类里面的样本数据进行信息容纳冗余的减少。

109、有益效果

110、(1)主动学习策略和自构造神经网络的半监督软测量，首先引入对输入空间划分更为灵活的非对称高斯函数作为隶属函数，增强非线性系统模糊规则的表征能力；建立sofnn-hps模型。

111、(2)本发明主动学习策略的半监督方式，通过核k-means聚类、距离度量准则以及高斯回归模型对大量无标签数据进行数据样本选择，选出价值量较大的样本对有标签数据集进行数据增强，再用sofnn-hps模型对未更新有标签数据集以及已更新有标签数据集进行训练，预测出水氨氮浓度；已更新有标签数据集能够提高软测量模型的性能。