基于离散微分几何理论的光路动力学应力计算方法
本发明涉及光纤动力,特别是涉及一种基于离散微分几何理论的光路动力学应力计算方法。
背景技术:
1、光纤陀螺仪是一种基于萨格纳克效应的角速度传感器,是惯性导航系统的核心部件之一。它以全固态、高精度、高稳定和低成本等优点在航空航天、船舶及军事等领域得到广泛的应用。而光纤线缆作为光纤陀螺的信号传输,其内部应力大小及分布直接影响着光纤陀螺的整体性能。因此,光路的低应力装配是实现光纤陀螺光路自动化装配与大批量生产的关键手段。
2、在光纤陀螺光路的应力研究中,杨远洪等首次提出将布里渊光时域反射原理作为光纤应力分析仪并对光纤进行了应力分析与测试,随后基于这种光纤应力分析仪,尹其其等研究了光纤绕制工艺和固化工艺对光纤应力的影响,而邱红芳则通过理论与实验证明光纤环圈中拐点处的应力更大,对光纤环圈的性能影响更大。然而对于在地震检测及世界时测量等方面的大型光纤陀螺,其光纤环长度可达数千米,应力分析仪很难准确测量;而工程化的微小型光纤陀螺又因其尺寸过小容易造成测量上的误差。
3、此外在光纤陀螺的装配工艺中,王晖等提出了自动微装配技术在微小型光纤陀螺批量装配生产的优势,ge等基于光电器件的精密机械定位方法实现了光纤自动排布与卷绕控制技术,而刘元元等通过建立光路损耗不等式约束条件来避免落入光路损耗区域,提高了光纤装配成功率。目前,对于光纤陀螺的光纤装配仍存在着低应力装配定量控制的难题;进行光纤动力学仿真应力对于实现光纤陀螺光路低应力装配的定量控制至关重要。
技术实现思路
1、基于上述问题,本发明实施例提供了一种基于离散微分几何理论的光路动力学应力计算方法。
2、本发明实施例提供的一种基于离散微分几何理论的光路动力学应力计算方法,包括:
3、s1、建立光纤的几何表示形式,并基于几何特性确定包括光纤拉伸应变、弯曲应变以及扭转应变的光纤运动学框架;
4、s2、将光纤离散化为多个节点和圆柱线段,确定表征离散化后光纤位姿的广义坐标系,并结合光纤运动学框架得到离散化后光纤每个线段上的拉伸应变以及每个节点上的弯曲应变、扭转应变;
5、s3、利用离散化后得到的拉伸应变、弯曲应变和扭转应变分别计算光纤的拉伸弹性势能、弯曲弹性势能以及扭转弹性势能;
6、s4、利用光纤的拉伸弹性势能、弯曲弹性势能以及扭转弹性势能得到描述光纤中每个节点上的拉伸力、弯曲力、扭转力及每条线段上的扭矩,并由节点上的力计算出轴向应力和切向应力;
7、s5、确定广义外力、广义速度阻尼力以及广义质量矩阵,由牛顿定律得到包含广义弹性力、广义外力、广义速度阻尼力以及广义质量矩阵的光纤动力学方程;
8、s6、为保证动力学方程求解的稳定性,基于newmark隐式算法建立当前时刻的广义外力与光纤下一时刻的广义位移、广义速度以及广义加速度之间的运算关系,从而得到下一时刻的广义加速度、广义速度及广义位移;
9、s7、由广义位移与广义坐标系之间的计算关系得到下一时刻光纤的广义坐标系,最后参照s2-s4得到下一时刻光纤节点上的力,以及下一时刻光纤上的轴向应力与切向应力。
10、可选的,s1具体包括:
11、假设光纤由一条中心线和一系列均匀各向筒形的圆形截面组成,且中心线穿过每个圆形截面的几何中心;
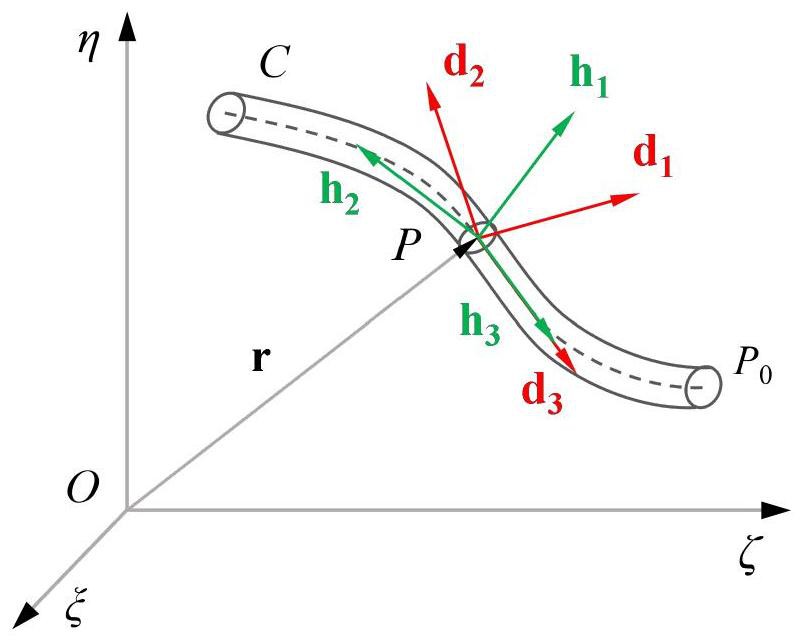
12、在全局坐标系(o-ξζη)中用向量r(s,t)表示光纤的中心线c,其中s是以中心线的一端为原点建立的弧坐标系,t为时间,则中心线的运动学可由其运动速度与变形梯度表示;
13、为描述光纤的弯扭状态,定义一个与刚性横截面固连的材料框架{d1(s,t),d2(s,t),d3(s,t)},三个单位向量dk(k=1,2,3)两两互相垂直,且d3=d1×d2是横截面的单位法向量;
14、对于细长光纤忽略其剪切变形,则光纤横截面始终与中心线正交,即横截面的单位法向量与中心线切线方向的单位矢量t重合:
15、
16、则光纤的拉伸应变εe表示为:
17、εe=r′·d3=|r′|
18、根据无穷小旋转的定义,材料框架{d1,d2,d3}在空间上沿弧长s的变化d′k(k=1,2,3)和在时间上的变化为:
19、d′k=ω×dk,
20、其中,ω表示光纤的弯扭度矢量,ω表示光纤的角速度矢量,具体的:
21、ω=d3×d′3+(d1′·d2)d3
22、
23、在不考虑剪切应变的情况下,弯扭度矢量ω与角速度矢量ω可表示为:
24、ω=t×t′+(d1′·d2)t=kb+ω3t
25、
26、其中,kb=t×t′为中心线副法线曲率,k=|t′|为曲率大小,b=t×t′/|t′|为副法线方向的单位矢量,ω3=d′1·d2为扭转应变,为扭转角速度,则光纤的弯曲应变、扭转应变分别表示为:
27、εb=|ω-(ω·t)t|=k,εt=|ω·t =ω3
28、可选的,s2具体包括:
29、采用中心线和自适应框架组合的方式来表示材料框架的位置和方向,其中,中心线的自适应框架{h1,h2,h3}用空间平行框架和时间平行框架a={a1,a2,t}表示,空间平行框架的弯扭度矢量ωb和时间平行框架的角速度矢量ωa分别表示为:
30、ωb=kb,
31、进一步将光纤离散为n+2个节点(0,1,…n+1)和n+1个圆柱线段(0,1,…n),离散节点均匀分布,节点坐标表示为xi={xi,yi,zi},光纤第i条线段的切向量为si=xi+1-xi,对应单位切向量为ti=si/|si|,每个光纤线段上材料框架与时间平行框架之间的夹角为θi,离散化后光纤位姿的广义坐标系表示为x,x={x0,θ0,x1,θ1,...,xn,θn,xn+1}t,大小为4n+7;
32、离散化后光纤第i条线段的拉伸应变表示为:
33、
34、其中|si|和分别为第i条线段的当前长度和初始长度;
35、离散化后第i个节点的弯曲应变、扭转应变分别表示为:
36、
37、其中为第i个节点的沃洛诺伊图区域长度,即第i-1条线段和第i条线段长度之和的一半;αi为第i个节点的离散扭转角;ki为第i个节点的副法线曲率;κi为第i个节点的离散积分曲率定义为:
38、
39、其中,为相邻线段i-1和i之间的夹角。
40、可选的,
41、为了计算离散扭转角αi,引入平行传递的概念,由于空间平行框架只取决于中心线位置,因此空间平行框架之间的平行传递为:
42、
43、将材料框架{d1,d2,d3}和空间平行框架{b1,b2,t}从第i-1条线段平行传递到第i条线段,得到离散扭转角:
44、
45、其中,和分别为相邻的第i-1条线段和第i条线段上的材料框架与空间平行框架之间的夹角;
46、同理,同一线段上的时间平行框架也具有平行传递关系:
47、
48、将时间平行框架的向量进行空间上的平行传递,得到向量使得向量和夹角为βi-1,即与第i-1条线段上的空间平行框架和时间平行框架之间的夹角保持一致;
49、最后确定第i个节点的离散扭转角计算为:
50、
51、其中,为相邻向量和之间的夹角。
52、可选的,s3具体包括:
53、在不考虑剪切变形的情况下,光纤的弹性势能eel包括拉伸弹性势能ee(el)、弯曲弹性势能eb(el)和扭转弹性势能et(el),离散化形式为:
54、
55、其中,ee、eb和g分别为光纤的拉伸模量、弯曲模量和剪切模量,ai为第i条线段上的横截面积;ii和ip,i分别为第i个节点上的截面惯性矩和极惯性矩;和分别为第i个节点上沃洛诺伊图区域在初始时刻的弯曲应变、扭转应变、离散积分曲率和离散扭转角。
56、可选的,s4具体包括:
57、拉伸弹性势能ee(el)、弯曲弹性势能eb(el)和扭转弹性势能et(el)分别对光纤节点坐标xi求偏导得到拉伸力弯曲力和扭转力扭转弹性势能et(el)对角度θi求偏导得到扭矩
58、
59、计算节点弹性力利用计算得到的节点弹性力计算光纤在第i个节点受到的轴向应力和切向应力
60、
61、其中,分别为第i个节点的轴向弹性力和切向弹性力,a表示节点处的截面面积。
62、可选的,s5具体包括:
63、确定广义弹性力fel的列向量表示为:
64、
65、确定广义外力fext、广义速度阻尼力fd以及广义质量矩阵m,并根据牛顿定律建立总的动力学方程:
66、m·a=fel+fd+fext
67、其中,a为广义加速度的列向量;
68、基于所建立的动力学方程计算当前广义加速度的列向量a。
69、可选的,s6具体包括:
70、将总的动力学方程改写为二阶矩阵形式:
71、
72、其中,u(tn+1)、和分别为下一时刻tn+1的未知广义位移、广义速度和广义加速度,fext(tn)为当前时刻tn已知的广义外力,d为速度阻尼刚度矩阵,即对角线上元素为阻尼系数的对角矩阵,k为弹性刚度矩阵,由广义弹性力fel线性化得到:
73、
74、其中,bel(tn)=fel(tn)-ku(tn)为常数项;
75、采用newmark算法计算下一时刻的广义位移和广义加速度的预测值:
76、
77、
78、其中,取权重系数λ1=1/2和λ2=1/4,得到梯形规则下时间步长的无条件稳定性,并最终得到下一时刻的广义加速度广义速度及广义位移
79、
80、
81、
82、可选的,s7中具体包括:
83、广义位移u包括节点位移和线段扭转角:
84、u={u1,β1,u2,β2,...,un,βn,un+1}
85、其中,ui={ui,vi,wi}为第i个节点的位移,βi为第i条线段的扭转角,因此得到广义位移u与广义坐标系x之间的关系为:
86、{xi(tn+1),θi(tn+1)}={xi(0),θi(0)}+{ui(tn+1),βi(tn+1)}。
87、可选的,s5中确定广义外力的过程包括:
88、确定光纤是否与周围物体产生碰撞,产生碰撞情况下,光纤节点会受到碰撞物体的接触力包括法向支撑力和切向摩擦力
89、
90、其中,法向支撑力使得节点沿接触面法向的受力和速度为零,则碰撞后的法向支撑力和节点切向速度为:
91、
92、
93、其中,为节点重力,为节点弹性力,vi为节点碰撞前的速度,为节点法向速度;
94、对于切向摩擦力若节点碰撞后的速度不为零或者碰撞后节点所受切向力大于最大静摩擦力ks为静摩擦系数,则节点受到切向摩擦力为:
95、
96、其中,kd为动摩擦系数;若节点碰撞后速度为零且碰撞后节点所受切向力小于最大静摩擦,则节点保持静止,切向摩擦力为:
97、
98、最后根据节点受到碰撞物体的接触力和重力确定广义外力。
99、与现有技术相比,本发明的有益效果在于:基于离散微分几何理论建立了光纤运动学框架,能够在简化光纤自由端并降低计算量的同时,保证计算结构具有良好的鲁棒性与精度;随后基于运动学框架由弹性势能推导出描述光纤装配过程中拉伸力、弯曲力、扭转力、扭矩、轴向应力和切向应力的动力学模型;基于newmark隐式算法提出了预测下一时刻光纤位姿的动力学稳定求解方法;此外研究了碰撞检测以及接触力的碰撞响应策略,实现了光纤装配仿真的稳定计算与物理意义上的接触碰撞响应效果。
- 还没有人留言评论。精彩留言会获得点赞!