一种含层理岩体三向应力解算方法

本发明属于岩体应力测量领域，特别涉及一种含层理岩体三向应力解算方法。

背景技术：

1、大量研究表明，岩体应力是引起各种地下工程变形及工程灾害的驱动力，准确监测三向应力的变化是工程围岩稳定性分析，安全生产的前提。

2、目前，岩体应力测量方法分为直接测量法与间接测量法，如水压致裂法、空心包体应变法、声发射法等。但水压致裂只能测得与钻孔轴线垂直截面上的应力分量，无法测得岩体三向应力；声发射法对岩体质量要求较高，且kaiser点存在多解性和应力失效区间，应用较为局限；空心包体应变法仅考虑岩体为均质各向同性，且对温度、黏结材料变形等其他因素考虑较少，仅能测得某一时刻岩体中的应力，不能实现连续测量。

技术实现思路

1、本技术旨在至少在一定程度上解决相关技术中的技术问题之一，本发明实施例提供了一种含层理岩体三向应力解算方法，考虑多重因素，包括黏结材料变形等因素对三向应力进行修正，具体方案如下：

2、一种含层理岩体三向应力解算方法，包括：

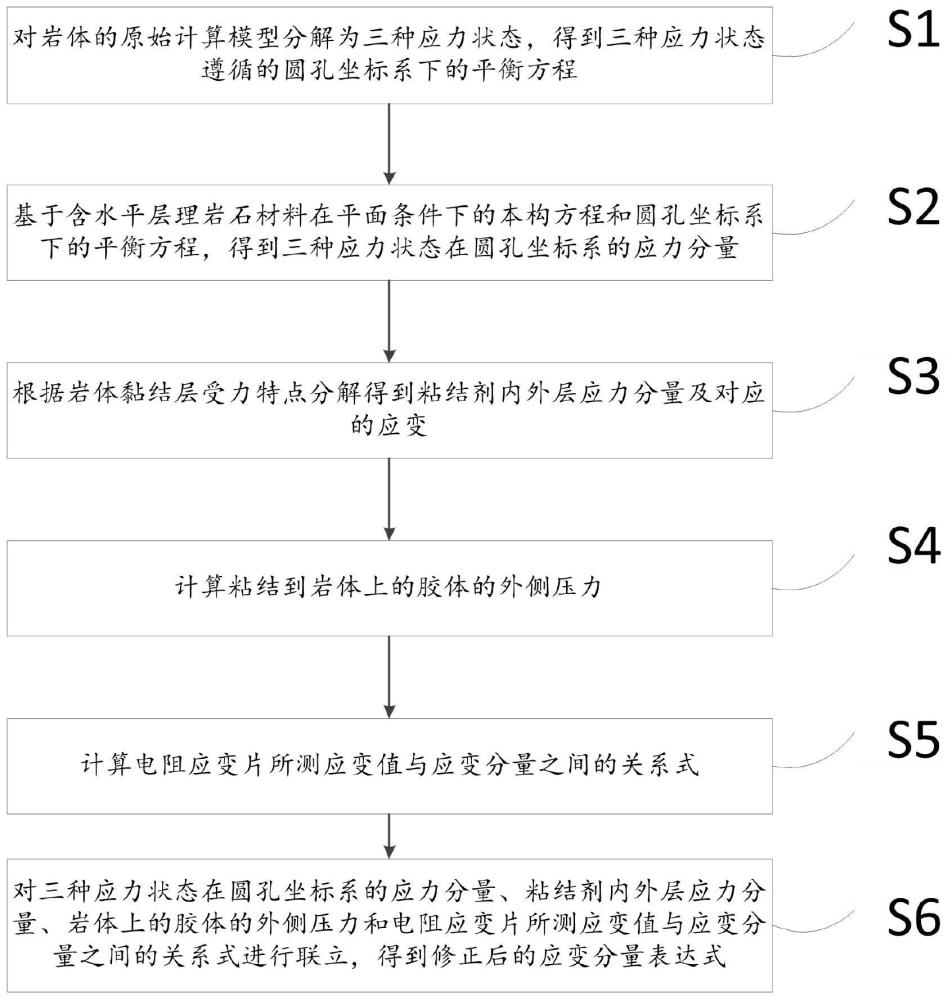
3、s1、对岩体的原始计算模型分解为三种应力状态，得到三种应力状态遵循的圆孔坐标系下的平衡方程；

4、其中，所述三种应力状态包括：yz向正应力与切应力状态、轴向应力状态和纯切应力状态；

5、s2、基于含水平层理岩石材料在平面条件下的本构方程和圆孔坐标系下的平衡方程，得到三种应力状态在圆孔坐标系的应力分量；

6、s3、根据岩体黏结层受力特点分解得到粘结剂内外层应力分量及对应的应变；

7、s4、计算粘结到岩体上的胶体的外侧压力；

8、s5、计算电阻应变片所测应变值与应变风量之间的关系式；

9、s6、对三种应力状态在圆孔坐标系的应力分量、粘结剂内外层应力分量、岩体上的胶体的外侧压力和电阻应变片所测应变值与应变分量之间的关系式进行联立，得到修正后的应力分量表达式；

10、s7、考虑实际的层理倾角，对应力分量进一步修正。

11、可选地，所述s1中的对岩体的原始计算模型分解为三种应力状态，得到三种应力状态遵循的圆孔坐标系下的平衡方程包括：

12、对岩体的原始计算模型分解为yz向正应力与切应力状态、轴向应力状态和纯切应力状态；

13、yz向正应力与切应力状态、轴向应力状态和切应力状态满足圆孔坐标系下的平衡方程为公式(1)：

14、

15、其中，σr为圆孔坐标系下径向应力，σθ为圆孔坐标系下环向应力，τrθ为圆孔坐标系下切应力，为极径r与极角θ的应力函数表达式。

16、可选地，所述s2的基于含水平层理岩石材料在平面条件下的本构方程和圆孔坐标系下的平衡方程，得到三种应力状态在圆孔坐标系的应力分量包括：

17、s201、将yz向正应力与切应力状态定义为横观各向同性体，根据岩石材料的本构方程及广义胡克定律，得到yz向正应力与切应力状态下的含水平层理岩石材料在平面条件下的本构方程，其中，yz向正应力与切应力状态下的含水平层理岩石材料在平面条件下的本构方程的公式为公式(2):

18、

19、其中，σy为y方向的正应力，σz为z方向的正应力，τyz为直角坐标系下yoz平面上的切应力，εy为σy对应的应变，εz为σz对应的应变，γy为τyz对应的应变；

20、其中，

21、

22、

23、其中，ex为沿x坐标轴方向的弹性模量；ey为沿y坐标轴方向的弹性模量；ez为沿z坐标轴方向的弹性模量；μxz、μxy、μyz分别为xz、xy、yz平面下的泊松比；gyz为平行于y-z平面下的剪切模量；

24、s202、对所述yz向正应力与切应力状态进行应力分解，基于所述yz向正应力与切应力状态下的含水平层理岩石材料在平面条件下的本构方程，得到所述yz向正应力与切应力状态下的形变势能表达式；

25、s203、分别构造所述yz向正应力与切应力状态的应力分解后的应力下的孔周应力函数表达式；

26、s204、将所述yz向正应力与切应力状态的应力分解后的应力下的应力函数表达式与所述yz向正应力与切应力状态下的形变势能表达式联立，得到所述yz向正应力与切应力状态的应力分量；

27、s205、计算轴向应力状态和切应力状态下单独受力情况下孔口周边围岩应力分布，得到钻孔坐标系下x向应力及其余切应力。

28、可选地，所述s202的对所述yz向正应力与切应力状态进行应力分解，基于所述yz向正应力与切应力状态下的含水平层理岩石材料在平面条件下的本构方程，得到所述yz向正应力与切应力状态下的形变势能表达式包括：

29、s2021、对所述yz向正应力与切应力状态进行应力分解，将所述yz向正应力与切应力状态下的含水平层理岩石材料在平面条件下的本构方程代入形变势能的表达式，得到应变余能表达式，所述应变余能表达式v为公式(3)：

30、

31、s2022、获取应力函数表达式，应力函数表达式为公式(4)：

32、

33、其中，为设定的函数，大小等于给定应力边界条线下的应力分量；为无面力时应力边界条件下的应力分量；α2为互相独立的两个系数，用来实现形变势能的变分；

34、s2023、根据应变余能表达式v和应力函数表达式进行形变势能变分，得到形变势能表达式，所述形变势能表达式为公式(5)：

35、

36、可选地，所述s203中所述yz向正应力与切应力状态的应力分解后的应力下的的应力函数表达式为公式(6)至公式(9)：

37、

38、

39、

40、

41、其中，分别为yz向正应力与切应力状态的应力分解后的四种情况下的孔周应力函数表达式；p0为钻孔内侧提供的支持力；a为钻孔内侧半径；

42、α1、α2、β1、β2、χ1、χ2和c0为变分系数,通过变分系数实现形变势能的变分；

43、所述s204的将所述yz向正应力与切应力状态的应力分解后的应力下的极径和极角的应力函数表达式与所述yz向正应力与切应力状态下的形变势能表达式联立，得到所述yz向正应力与切应力状态的应力分量包括：

44、s2041、联立所述yz向正应力与切应力状态的应力分解后的应力函数表达式与所述yz向正应力与切应力状态下的形变势能表达式，得到七个变分系数的表达式，所述七个待定系数的表达式分别为公式(10)至公式(16)：

45、

46、

47、

48、

49、

50、

51、

52、其中，所述yz向正应力与切应力状态的应力分解后得到：只受孔内支持力状态、只受拉力状态、一侧受拉力另一侧受压力状态和只受切向力状态；

53、s2042、根据所述七个待定系数的表达式，基于应力叠加原理，得到a＝r时的应力分量表达式，其中，到a＝r时的应力分量表达式包括公式(17)至公式(19)：

54、σr＝σr1+σr2+σr3+σr4＝-p0 (17)

55、σθ＝σθ1+σθ2+σθ3+σθ4＝p0[1-2(α1+α2)sin22θ]-(σy+σz)-2(σy+σz)(β1+β2)cos2θ+(σz-σy)(2+2χ1+2χ2)cos2θ-τyz(4+4c0)sin2θ (18)

56、τrθ＝0       (19)

57、其中，σr1为只受孔内支持力状态的孔口径向应力分量；σr2为只受拉力状态的孔口径向应力分量；σr3为一侧受拉力另一侧受压力状态的孔口径向应力分量；σr4为只受切向力状态的孔口径向应力分量；σθ1为只受孔内支持力状态的切向应力分量；σθ2为只受拉力状态的切向应力分量；σθ3为一侧受拉力另一侧受压力状态的切向应力分量；σθ4为只受切向力状态的切向应力分量。

58、可选地，所述s205中的计算轴向应力状态和切应力状态下单独受力情况下孔口周边围岩应力分布，得到钻孔坐标系下x向应力及切应力包括：

59、钻孔坐标系下x向应力的公式为公式(20)：

60、

61、其中，τyz为直角坐标系下yoz平面上的切应力；ux为与层理平行方向的泊松比；σx′为钻孔坐标系下x向应力，

62、所述钻孔坐标系下x向切应力的计算公式为公式(21)至公式(22)：

63、

64、

65、其中，τθx为环向应力面上沿x方向的切应力；τrx为径向应力作用面上沿x方向的切应力；τyx为直角坐标系下yox平面上的切应力；τxz为直角坐标系下zox平面上的切应力。

66、可选地，所述s3中的根据岩体粘结层受力特点得到粘结剂内外层应力分量及对应的应变包括：

67、外层径向应力分量σr外及径向应变εr外的计算公式为：

68、

69、外层环向应力分量σθ外的计算公式为：

70、

71、其中，e0为黏结剂弹性模量，u0为黏结剂泊松比，r1为黏结层外径，r2为黏结层内径；

72、内层径向应力分量σr内的计算公式为：

73、σr内＝0

74、内层环向应力分量σθ内及内层应变ε′θ内的计算公式为：

75、

76、可选地，所述s4中计算粘结到岩体上的胶体的外侧压力包括：

77、基于应变边界条件：εr外＝εr孔，其中，εr孔为钻孔径向应变，通过获得；u为r-θ平面内泊松比的均值；

78、计算岩体上的胶体的外侧压力p0的计算公式为公式(23)：

79、

80、其中，u为r-θ平面内泊松比的均值，eφ为不同层理倾角对应的弹性模量；

81、其中，eφ的计算公式为公式(24)：

82、

83、其中，

84、e1为平行于层理面的弹性模量；e2为垂直于层理面的弹性模量；μ2为垂直于各层理面方向的泊松比；g2为垂直于各层理面方向的剪切模量；φ表示为层理倾角；f1、f2和f3为岩石弹性模量的修正的待定系数。

85、可选地，所述s5的计算电阻应变片所测应变值与应变风量之间的关系式包括：

86、按照公式(25)计算应变片的形变：

87、

88、化简求得公式(25)得到:

89、

90、其中，eai、ebi、eci分别为第i组应变片φa＝0、时所对应的形变；εθi、εxi、γθxi为第i组应变片对应孔壁位置处的环向应变、轴向应变及切应变。

91、可选地，所述s6中对三种应力状态在圆孔坐标系的应力分量、粘结剂内外层应力分量、岩体上的胶体的外侧压力和电阻应变片所测应变值与应变分量之间的关系式进行联立，得到修正后的应力分量表达式为公式(26)至(31)：

92、

93、

94、

95、

96、

97、

98、其中，

99、

100、

101、eai、ebi、eci分别为第i组不同角度应变片的形变，etφ为与温度及层理倾角有关的岩石弹性模量，由下式确定：

102、etφ＝eφ+ω1t2+ω2t

103、ω1、ω2为温度系数，通过室内试验拟合获得，t为温度；et(0°)、et(120°)、et(240°)分别为t温度下层理为0度、120度及240度时对应的弹性模量。

104、本发明实施例提供的技术方案带来的有益效果至少包括：

105、本方法通过考虑岩体横观各向同性、温度及粘结剂变形的影响，更加准确得到岩体中的三维应力，利用横观各向同性体的弹性力学理论及应力变分法，推导出钻孔地应力测量时孔周应力分部规律，计算粘结层形变，更加准确得到岩体中的三维应力，消除了之前方法仅将钻孔周围岩体视为均质各向同性体所带来的误差，为确定工程岩体力学属性、进行围岩稳定性分析、实现岩石工程开挖设计及地应力场反演提供更为可靠的依据。

106、复杂地应力会对矿井安全生产产生严重影响，与煤与瓦斯突出、冲击地压、矿井突水等矿井地质灾害现象有着非常密切的关系，因此准确掌握矿井地应力的分布特征,对于防控地质灾害、实现矿井布置最优化设计有着极其重要的意义，准确的测量结果可以有效提高工作的安全性。