基于传输线法的三维电磁继电器多场耦合并行计算方法

本发明属于数值计算领域，涉及一种适用于电器产品电磁系统的三维多物理场耦合数值计算方法，具体涉及一种基于传输线法(transmission line method,tlm)的三维多物理场耦合的有限元并行计算方法。

背景技术：

1、航天电磁继电器具有高转换深度、优良的物理隔离性、可多路同步切换等优点，在航天工程中应用量大、面广，是完成信号传递、执行控制、系统配电和保护等功能的关键电子元器件，其技术水平代表了电磁继电器的最高水平。相对其他的电子产品而言，航天电磁继电器是由电磁机构、接触单元构成的复杂机电系统，内部往往包含磁性、弹性、绝缘材料，且工作过程涉及电、磁、热、力、流体等多物理场耦合作用，零部件众多、工艺复杂。航天电磁继电器在所有电子元器件门类中质量与可靠性最差，尤其在耐环境可靠性方面不同产品之间的差异明显，严重制约了航天工程的发展。

2、与传统的实验测量相比，尽管数字样机模型与实验测量相结合的方案可以灵活、有效地测量和评估动态特性，但现有的商用有限元软件在计算三维数字样机模型的动态特性时存在耗时长、收敛性差等问题，极大地影响了航天电磁继电器的设计和生产周期。航天电磁继电器产品设计分为总体设计、参数设计和容差设计三个阶段进行，简称为三次设计。通过三次设计，才能从设计源头保证所设计的产品具有长寿命、高可靠性的特点。三次设计需要不断地对模型参数进行调整，每次调整完后需要重新求解数字样机模型以优化性能参数，优化设计过程中重复的仿真计算需要耗费大量的时间。因此，数字样机模型的计算准确性和求解效率对于航天电磁继电器三次设计至关重要。

3、有限元法(finite element method,fem)作为数字样机模型的核心技术，被广泛应用于电器领域的仿真分析中。有限元法的计算精度和速度很大程度上决定了基于数字样机技术的电器优化设计的效率。相较于二维问题，三维电磁场的求解方法具有较大的差异，并且目前三维多物理场耦合模型的数值算法仍存在计算效率低的问题。因此，将加速算法推广至三维有限元模型的求解中具有重要意义。航天电磁继电器的动作过程涉及电磁-热-力的多物理场耦合计算，不同温度环境对动态特性的影响也非常显著。对单一物理场的求解已不能满足航天电磁继电器的实际生产需求。然而，多物理场耦合的数字样机模型相较于单场模型需要花费更多的时间进行求解，其求解效率直接影响到航天电磁继电器的设计和生产周期。因此，研究多物理场耦合的有限元并行计算具有重要的实际和工程意义。

技术实现思路

1、本发明的目的是提供一种基于传输线法的三维电磁继电器多场耦合并行计算方法，该方法以实现加速求解电器三维多场耦合的数字样机模型为目标，意在填补电器三维数字样机模型电磁-热-力多物理场耦合建模多学科交叉、并行数值计算的空缺。本发明主要针对三维航天电磁继电器多物理场耦合的动态特性进行并行求解，采用棱边有限元法建立了航天电磁继电器的三维电磁-热-力多物理场耦合模型，并将tlm引入到三维多物理场耦合的有限元模型求解中，达到加速求解动态特性的目的。本发明可直接应用于航天电磁继电器的三维数字样机模型的仿真计算，对于提高航天电磁继电器的耐环境可靠性设计具有重要的理论意义，对缩短航天电磁继电器结构设计及参数优化周期也具有借鉴意义。

2、本发明的目的是通过以下技术方案实现的：

3、一种基于传输线法的三维电磁继电器多场耦合并行计算方法，包括如下步骤：

4、步骤一、建立航天电磁继电器的三维电磁-热-力多场耦合数字样机模型：

5、步骤一一、根据航天电磁继电器电磁系统的几何尺寸建立其三维有限元模型，将求解域离散为有限个大小和形状相连的四面体单元，并根据求解精度的需要对其网格数量进行控制，完成有限元模型的网格剖分；

6、步骤一二、将三维有限元模型的网格信息导出并解析，得到包含网格的四面体单元数、节点数和单元所属区域，以及四面体单元的节点坐标和节点编号网格信息，并计算所有四面体单元的棱长；

7、步骤一三、当航天电磁继电器的线圈上电后会产生磁场，瞬态磁场由矢量磁位a进行描述，其控制方程为：

8、

9、式中，a为矢量磁位；ν为磁阻率；σ为电导率；je为线圈电流密度；t为时间；

10、步骤一四、采用棱边有限元法求解三维有限元模型：

11、步骤一四一、将整个三维求解区域ω拆分成许多较小的四面体单元和四面体之间的棱，对于四面体单元ωe内任一点的矢量磁位向量ae(x,y,z)，用已知插值函数的线性组合来近似表示：

12、

13、式中，i为四面体单元的棱边数量；wi(x,y,z)为基于棱边向量的插值函数；为矢量磁位场a(x,y,z)沿着第i条棱边方向上的线积分；插值函数wi仅由四面体单元的四个节点位置坐标决定，wi在棱边i上的投影为1，而在其余所有棱边上的投影则为0；

14、步骤一四二、四面体单元第k(k＝1,2,…,6)条棱所对应的棱边向量形函数wk及其旋度表示为：

15、

16、式中，lij表示节点i和节点j之间的棱长，其正负由方向向量确定；n1、n2、n3和n4表示四面体单元的体积坐标；▽n1、▽n2、▽n3和▽n4表示四面体单元体积坐标的梯度；

17、步骤一四三、四面体单元体积坐标的梯度表示为：

18、

19、式中，ve为四面体单元的体积；为四面体单元六条棱的棱边矢量；

20、步骤一四四、对于一个单独的四面体单元ωe，其四个节点编号用n＝1,2,3,4来表示，则四面体单元的体积v可由下式计算：

21、

22、式中，xn,yn,zn分别是四面体单元中四个节点所对应的x,y,z坐标。

23、步骤一四五、通过galerkin法对残差与6个加权函数wi的乘积进行积分，并强制积分为零，在考虑库伦规范后，得到10×10矩阵形式的单元离散方程：

24、

25、其中

26、

27、

28、式中，ni为四面体单元的体积坐标；je为线圈电流密度，线圈电流可通过场路耦合获得；aj为矢量磁位场a沿着第j条棱边方向上的线积分；

29、步骤一四六、建立三维瞬态磁场的传输线模型，用于求解步骤一四五的磁场方程，具体步骤如下：

30、传输线法将三维非线性系统解耦为线性网络和非线性网络，得到传输线模型的等效电路，该等效电路包含入射阶段和反射阶段的电路模型，两个阶段在线性网络和非线性网络交替进行，直至收敛，从而完成三维非线性系统的求解，其中：

31、(1)步骤一四五的磁场公式中子矩阵[kij]6×6和[dij]6×6等效电路模型的非线性电阻和线性电容表示为：

32、

33、(2)非线性电阻在反射阶段由传输线和反射盒取代，传输线的特征电导由下式表示：

34、

35、(3)线性电容与非线性电阻并联，电磁场的时间导数与电容有关，电容通过后向欧拉法用电阻和上一时刻的电流源代替，导纳和电流源的计算公式为：

36、ycij＝cij/δt,yci＝ci/δt,i,j∈[1,6]

37、

38、

39、(4)在入射阶段，受节点电压ai和支路电压(ai-aj)影响的入射电压进入反射盒，在每个反射盒内，一个端口的入射电压会根据非线性电阻的耦合关系散射到所有端口，反射阶段结束后，入射电压离开反射盒成为反射电压，入射电压和反射电压之间的非线性关系表示为：

40、

41、采用nr迭代来求解这个6×6的方程组，并根据链式法则计算雅可比矩阵：

42、

43、通过nr迭代求解6×6的方程组后，得到单元磁阻率νe的值；

44、(5)在入射阶段，包含单元非线性电阻信息的反射电压返回至全局电路网络，传输线和反射电压由诺顿电路取代，然后通过线性网络更新全局电路网络的节点电压，并根据节点电压求出下一次迭代的入射电压，另外，入射阶段的电路网络是由网格中所有单元导纳和库伦规范装配而成的大规模线性网络，且在每个时间步的迭代过程中保持不变；

45、通过步骤一四六可并行求解获得磁场的矢量磁位分布；

46、步骤一四七、根据棱边元公式，对于每一个四面体单元，磁感应强度b通过矢量磁位a来进行表示，则三维非线性瞬态磁场方程表示为：

47、

48、步骤一五、采用场路间接耦合方案实现继电器电磁场和电路的耦合：

49、步骤一五一、航天电磁继电器线圈的方程表示为：

50、

51、式中，u为线圈电压，i为线圈电流，r为线圈电阻，ψ为励磁线圈的磁链；

52、步骤一五二、将步骤一五一中的公式改写为非线性方程的迭代形式：

53、f(t)＝ir+[ψ(t)-ψ(t-1)]/δt-u＝0

54、式中，ψ(t)为当前时间步的磁链，ψ(t-1)为上一时间步的磁链，δt为离散时间步长；

55、步骤一五三、根据三维fem模型获得线圈单元各条棱边的矢量磁位分布后，通过下式计算获得当前时间步的磁链：

56、

57、其中，ncoil为线圈匝数，scoil为线圈截面积，n为沿线圈电流方向的单位矢量，vcoil为线圈区域单元的体积，n为棱边的数目；

58、步骤一五四、采用牛顿迭代法将步骤一五二中的公式构造成下式的迭代格式，计算得到第(t+1)时刻的电流值i(t+1)，迭代格式如下：

59、

60、获得下一个时刻的电流值i(t+1)后代入瞬态磁场进行迭代计算，获得下一时刻的矢量磁位值，即可实现航天电磁继电器的电磁场和控制电路的场路耦合；

61、步骤一六、采用三维棱边元与单位载荷法相结合的方式推导电磁力和电磁力矩的并行计算方法：

62、步骤一六一、根据单位载荷法理论，电磁力表示为：

63、

64、式中，q为衔铁的位移方向，fq为衔铁在q方向受到的电磁力大小，wmag为磁场能量；

65、步骤一六二、在四面体单元e中节点k在x方向上的电磁力描述为：

66、

67、步骤一六三、结合三维非线性瞬态磁场方程，单元节点力fek化简为：

68、

69、式中，可以通过铁磁材料的b-h曲线获得，可以通过下式获得：

70、

71、步骤一六四、四面体单元的体积ve对xk的偏导数表示为：

72、

73、步骤一六五、在计算获得x方向上的电磁力后，同理计算获得y和z方向上的电磁力；电磁力和电磁力矩采用并行方案进行计算；

74、步骤一七、求解电磁场-机械运动耦合问题：

75、步骤一七一、在获得各个节点的电磁力后，根据下式计算各个节点的电磁力矩：

76、

77、式中，me为第e个单元的电磁力矩，为节点的电磁力大小，为作用点到转动轴的垂直距离，nn为每个单元的节点数目；

78、步骤一七二、将所有轮廓节点的电磁力矩进行累加，得到总电磁力矩：

79、

80、式中，mmag为作用于衔铁上的电磁力矩，ne为四面体单元的数目；

81、步骤一七三、计算获得电磁力矩后，航天电磁继电器的衔铁在旋转运动中的动力学方程描述为：

82、

83、式中，i为转动惯量，α为衔铁的角加速度，θ为衔铁的转动角度，mr为作用于衔铁上的机械阻力转矩；

84、步骤一八、航天电磁继电器的热传导有限元计算：

85、步骤一八一、瞬态温度场的三维偏微分方程表示为：

86、

87、式中，ρ为材料的密度，c为材料的比热容，t为固体或空气的温度，λ为介质的热导率，q为单位体积发热功率；

88、步骤一八二、用四面体的节点温度分布去表征温度场，采用fem的离散过程得到以下方程：

89、

90、上式用后向欧拉法进行时间离散化后，得到以下代数方程：

91、

92、式中，

93、

94、其中l,n＝1,2,3,4；为单元所在区域材料的密度，ce为单元所在区域材料的比热容，λe为单元介质的热导率，ge为内热源强度，pl、ql、rl和sl是与节点坐标x、y和z相关的函数；

95、步骤一八三、航天电磁继电器中的热源主要包含焦耳损耗和涡流损耗，其中涡流损耗peddy在磁场计算完毕后通过后处理的方式获得，表示为：

96、

97、式中，e为电场强度，ωcore为铁磁区域；

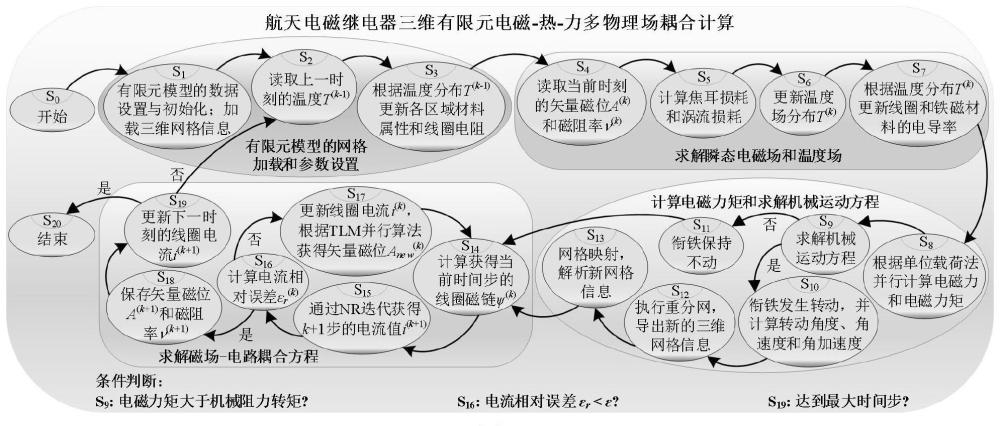
98、步骤二、航天电磁继电器三维有限元模型的电磁-热-力多场耦合数字样机模型的求解：

99、步骤二一、读取上一个时刻的温度分布并更新各个区域的材料属性；

100、步骤二二、读取当前时刻的矢量磁位分布和磁阻率，并计算焦耳损耗和涡流损耗；

101、步骤二三、计算温度场更新温度分布，并更新线圈和铁磁材料的电导率；

102、步骤二四、根据单位载荷法计算衔铁受到的电磁力和电磁转矩；

103、步骤二五、计算机械运动方程，判断衔铁是否发生转动，若发生转动则更新三维电磁-热-力多场耦合数字样机模型的网格信息，若衔铁保持不动则不需要更新网格信息；

104、步骤二六、根据场路耦合计算下一个时间步的线圈电流值，并保存下一个时间步的矢量磁位和磁阻率。

105、相比于现有技术，本发明具有如下优点：

106、(1)二维模型只能适用于对称结构或特定场合，但某些复杂三维几何结构无法在二维空间中进行表征，因此本发明采用棱边有限元法建立了航天电磁继电器的三维电磁-热-力多物理场耦合模型。相较于单场数字样机模型，多物理场耦合的三维数字样机模型可以综合考虑环境温度和内部温升对航天电磁继电器动态特性的影响，更贴近航天电磁继电器的实际工况。同时，将三维数字化建模技术与实验测量相结合的方法为电磁继电器动态特性的测试与评估提供了一种更经济和效率的新方案。

107、(2)本发明提出的三维数字样机模型实现了航天电磁继电器的电磁-热-力多物理场耦合，给出了航天电磁继电器三维多物理场耦合和并行求解的详细实施方案，并分析了温升对电磁继电器动态特性的影响。三维数字样机模型的动态特性评估结果与实验测量结果非常吻合，相对误差控制在4％以内。三维数字样机模型和实验测量相结合的方法为测量和评估航天电磁继电器的动态特性提供了更灵活和高效的方案。

108、(3)在求解三维多物理场耦合的有限元模型时，由于三维模型的网格数量较多，使用商用有限元软件计算动态特性所需的时间较长。本发明将tlm并行算法推广到三维多物理场耦合问题的求解中，将非线性混合网络解耦为线性网络和非线性网络，实现大规模并行计算。与商用有限元软件相比，tlm在求解三维多物理场耦合的动态特性时，计算速度最多提升了2.71倍，证明了所提三维多物理场耦合的动态特性加速方法的正确性和有效性，这将非常有利于快速测量和评估航天电器的动态特性。tlm非常适合三维大规模非线性问题的求解，随着计算机硬件并行计算能力的提升，tlm在三维多物理场耦合问题中的求解效率可得到进一步提升，具有良好的应用前景。

109、(4)本发明的三维数字样机建模的方法可以适用于其他不同结构的继电器和接触器，能广泛应用于电器产品的优化设计、电寿命试验等工程实践，具有较好的通用性和实用性。提出的并行计算方法可以缩短电器动态特性的评估时间，从而缩短产品的生产和优化周期，减小时间成本。另外，本发明可以进行成果转化，开发电器领域专业的三维有限元仿真软件，打破国外对有限元仿真软件的垄断，更进一步突显了本发明的有益效果与应用价值。