一种裂纹弥散特征尺寸协调的断裂相场方法

本发明属于断裂力学，涉及一种断裂相场法，具体涉及一种可以任意调节裂纹弥散特征尺寸使之与结构尺寸、单元尺寸相协调的断裂相场方法。

背景技术：

1、常用于航空航天领域的轻质、高强度材料大多数均为脆性材料。脆性材料在制备及服役过程中在复杂载荷、多物理场耦合效应等作用下，常因裂纹萌生及扩展而导致飞行器的可靠性及服役寿命大幅降低。研究脆性材料的断裂力学行为，对于飞行器的损伤容限设计至关重要。固体的断裂是一个高度非线性的物理过程，脆性材料的断裂往往是突发性的瞬间破坏，如何实现脆性断裂过程的仿真长期以来是一直是一个工程难题。

2、经典的仿真方法将裂纹处理为固体域内的不连续几何特征，如三维空间问题中的裂纹曲面，或二维平面问题内的裂纹曲线，这种具有几何不连续性的裂纹也被称为离散裂纹。基于离散裂纹的断裂力学数值计算手段有拓展有限元方法和重划分网格方法等。当涉及裂纹萌生及扩展问题的仿真时，这些方法需要额外的断裂准则来作为裂纹萌生及扩展的条件判据。然而，施加的断裂准则往往是非普适的，具有一定经验性。

3、断裂力学相场法克服了模拟裂纹萌生及扩展问题对额外的断裂准则的需求，它将经典的离散裂纹弥散化，并采用裂纹弥散特征尺寸参数来表征弥散裂纹区域的大小，使裂纹具备与所研究问题相同的维度。此外，断裂相场法满足热力学一致性，其控制方程由热力学推导获得，不再需要额外的断裂准则，可以通过在有限元网格上求解相场控制方程，自动实现裂纹萌生和扩展的模拟。在断裂相场法中，能量退化函数是刻画材料损伤规律的函数，经典脆性断裂相场法中的二次能量退化函数会导致材料参数与裂纹弥散特征尺寸之间的固定的映射关系。而这种映射关系由偏微分方程组的一维均匀解求得。为了正确地预测材料的极限强度，断裂相场法中的裂纹弥散特征尺寸参数需要按照映射关系取常数，这就限制了弥散裂纹区域的特征尺寸大小。这种对裂纹弥散特征尺寸的限制会导致断裂相场法在计算小尺寸结构时由于弥散裂纹区域尺寸过大而无法辨识裂纹萌生位置及裂纹扩展路径的不足。而对于大尺寸结构，固定的裂纹特征长度尺寸往往意味着庞大的网格数量以及计算代价，使得断裂相场法难以用于计算大尺寸结构。此外，由于弥散裂纹尺寸相对结构尺寸过小，而同样难以辨识裂纹扩展路径。这种裂纹弥散特征尺度与单元尺寸或结构尺寸的不协调，极大限制了断裂相场法在任意尺寸结构中的应用。

技术实现思路

1、为了弥补背景技术中研究存在的不足之处，本发明提供了一种裂纹弥散特征尺寸协调的断裂相场方法。该方法构建了一种材料参数与裂纹弥散特征尺寸之间可调映射关系，从而实现任意尺寸结构与裂纹弥散特征尺寸相协调。协调的裂纹弥散裂纹特征尺度可使得弥散裂纹区域的尺寸不会过大也不会过小，从而避免了网格数量过多或裂纹扩展路径难以识别的问题。本发明通过在相场法中的能量退化函数中引入可调的缩放因子s，来使得材料参数与裂纹弥散特征尺寸之间的映射关系可调，从而实现裂纹弥散特征尺度与结构尺寸、单元尺寸间的协调；基于有限元方法，对该模型进行数值实现，对比经典断裂力学相场法，验证了该方法获得协调的裂纹扩展路径的能力以及处理不同尺寸结构断裂问题的有效性。

2、本发明的目的是通过以下技术方案实现的：

3、一种裂纹弥散特征尺寸协调的断裂相场方法，包括如下步骤：

4、步骤一、建立经典脆性断裂相场法的理论框架：

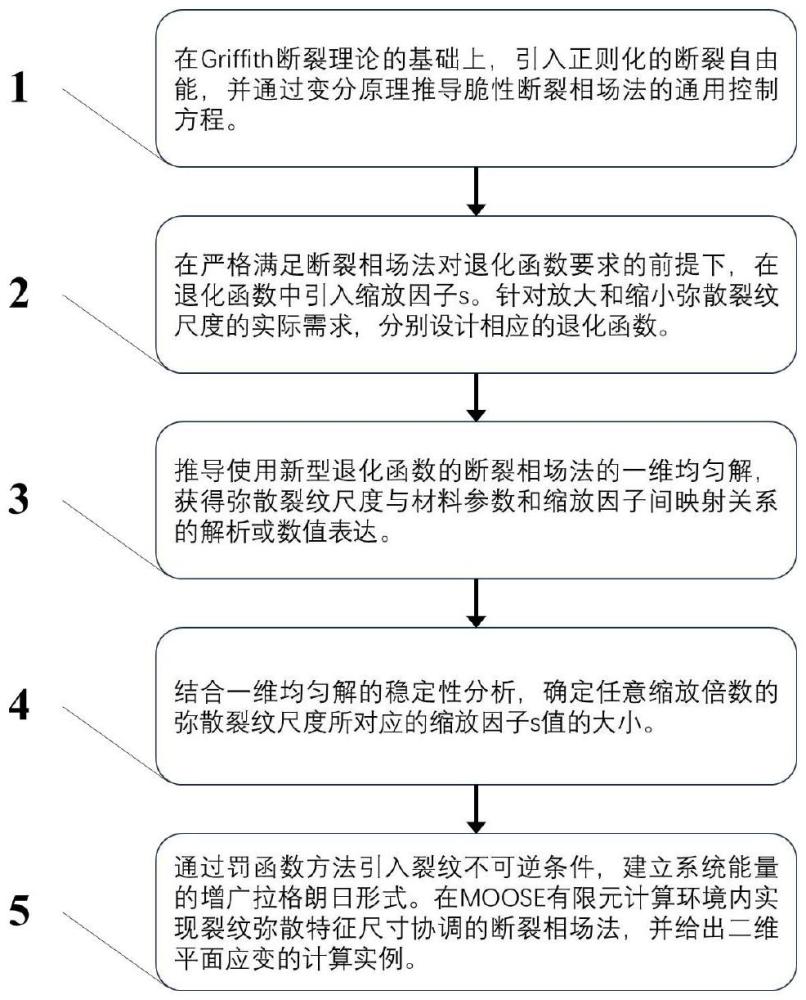
5、在griffith断裂理论的基础上，引入正则化的断裂自由能，建立脆性断裂相场法的能量泛函，并通过变分原理推导脆性断裂相场法的通用控制方程，具体步骤如下：

6、步骤一一、将经典griffith断裂力学的能量泛函弥散化，建立脆性断裂相场法的能量泛函：

7、

8、其中，ε为总势能泛函；u为弹性体的位移场；表示断裂相场的梯度；ω指求解域；g(d)为能量退化函数；为拉伸部分应变能；为压缩部分应变能；gc指临界断裂能量释放率；c0为几何系数；l0为断裂长度尺度；α(d)为几何函数；b指体力；t指面力；dx与ds分别指体积微元和面积微元；

9、步骤一二、通过变分法获得适用于三维脆性断裂问题的控制方程组：

10、力学平衡方程与应力边界条件：

11、

12、裂纹相场演化方程与相场边界条件：

13、

14、步骤二、建立裂纹弥散特征尺寸可调的能量退化函数：

15、在严格满足断裂相场法对退化函数要求的前提下，在退化函数中引入缩放因子s，针对放大和缩小裂纹弥散特征尺寸的实际需求，设计放大型能量退化函数gup(s,d)和缩小型能量退化函数gsd(s,d)：

16、

17、

18、步骤三、基于一维杆软化分析的极限强度解：

19、推导使用步骤二中建立的能量退化函数的断裂相场法的一维均匀解，获得裂纹弥散特征尺寸与材料参数和缩放因子间映射关系的解析或数值表达，具体步骤如下：

20、步骤三一、考虑步骤二中建立的能量退化函数，将步骤一中的控制方程退化为一维情况，可得：

21、

22、

23、式中，σx为轴向应力，εx为轴向应变，e为杨氏模量，为应变能；

24、步骤三二、求解上述一维的控制方程，可得轴向应力应变的解析解：

25、

26、步骤三三、通过对应力解进行一维稳定性分析，求解最大轴向应力对应的临界相场损伤值dc∈[0,1)；

27、步骤三四、求得临界损伤值后，代入轴向应力的解析表达式中即可获得极限强度，其中：

28、对于放大型能量退化函数，临界损伤值dc＝0恒成立，极限强度的表达式为：

29、

30、对于缩小型能量退化函数，若存在非0正数解，则需要根据一阶稳定性分析，计算临界损伤值dc，相应的控制方程为：

31、

32、求得临界损伤值后，带入轴向应力解，极限强度的表达式为：

33、

34、步骤四、特定裂纹弥散特征尺寸的调节：

35、结合一维均匀解的稳定性分析，确定任意缩放倍数的裂纹弥散特征尺寸所对应的缩放因子s值的大小：

36、

37、式中，dc为临界损伤值，l0*为缩放后的裂纹弥散特征尺寸，n为正数；

38、步骤五、裂纹弥散特征尺寸可调断裂相场法的有限元实现：

39、通过罚函数方法引入裂纹不可逆条件，建立系统能量的增广拉格朗日形式，在moose有限元计算环境内实现裂纹弥散特征尺寸可调的断裂相场法，具体步骤如下：

40、步骤五一、根据步骤一中建立的能量泛函，推导脆性断裂相场法积分方程的等效弱形式：

41、

42、式中，和为试函数；

43、步骤五二、为强制裂纹相场的不可逆性，引入额外的罚函数，建立增广拉格朗日形式：

44、

45、式中，γ>>1为拉格朗日乘子；

46、步骤五三、采用交替求解方案，依次求解平衡方程和相场演化方程，即：

47、

48、步骤五四、断裂相场法的有限元实现：

49、基于有限单元法，位移场与断裂相场的有限元插值表达式如下：

50、

51、

52、其中，{ui}代表位移列向量，{ui}＝[ux uy]t；m为一个单元的节点数目；nu为节点位移形函数矩阵；nd为节点断裂相场形函数矩阵；

53、则对应的形函数梯度矩阵为：

54、

55、

56、步骤五五、将有限元插值表达式分别代入步骤五一中的弱形式积分方程，分别得到如下节点力平衡方程和节点断裂相场驱动力平衡方程：

57、节点力平衡方程：kuu{ui}＝fu；

58、节点断裂相场驱动力平衡方程：kdd{di}＝fd；

59、其中，kuu为位移相关的刚度矩阵；kdd为断裂相场刚度矩阵；fu为节点力；fd为节点的断裂相场驱动力；各物理量表达式如下：

60、

61、

62、

63、

64、步骤五六、在开源有限元计算环境moose中编写有限元程序，在moose有限元计算环境内实现裂纹弥散特征尺寸可调的断裂相场法。

65、相比于现有技术，本发明具有如下优点：

66、1、首次系统提出了裂纹弥散特征尺寸任意可调的断裂相场法，打破了材料属性与裂纹弥散特征尺寸间固定映射的限制，使得对于同一种材料的断裂问题，可以采用任意的裂纹弥散特征尺寸进行模拟。

67、2、本发明的方法可以通过调节裂纹弥散特征尺寸使之与结构尺寸和网格尺寸相协调。根据实际计算需求，调整网格数量和弥散裂纹的分辨率。

68、3、本发明的方法具有良好的适用性与稳定性，容易在有限元方法中实现，实现了对二维平面应变下结构相场断裂问题的裂纹弥散特征尺寸调节。该方法可自然推广到三维问题，并可开发成商用程序以灵活适应所需问题的变化。