一种不同保温隔热措施下寒区无砟轨道板时变可靠度分析方法

本发明涉及铁路无砟轨道板，具体地说，涉及一种不同保温隔热措施下寒区无砟轨道板时变可靠度分析方法。

背景技术：

1、无砟轨道结构主要由混凝土等热的不良导体材料构成，温度传递性能差，在遭受外部环境剧烈温度变化时会导致内部温度分布不均，形成较大的温度梯度。受太阳辐射及轨道分层结构影响，温度梯度主要出现在垂向，造成轨道结构垂向的不均匀变形，如轨道板翘曲、上拱等，同时在结构内部产生较大的不均匀应力，在达到混凝土受拉强度极限时将产生受拉破坏，形成裂缝并不断发展。此外，在外界温度反复变化下，混凝土结构内部孔隙水会随之反复结冰、融化，导致内部损伤不断累积，结构逐渐从密实体向松散体转化，表现为混凝土强度的不断降低，严重影响无砟轨道服役的耐久性与可靠性。

2、面对着目前高速铁路无砟轨道高质量发展需求，寒区环境下其长期服役的稳定性与可靠性应得到准确把握。而无砟轨道结构设计使用年限为60年，这就要求设计使用年限内轨道结构有完成预定功能(耐久性、安全性、适用性)的能力，服役期间轨道结构失效将严重影响铁路运营的安全性，且考虑到外部荷载与结构自身强度变化具有随机性，是时间变量相关的随机过程，因此有必要引入时间变量，对寒区环境作用下无砟轨道荷载效应与可靠度进行分析，揭示设计年限内结构可靠度变化趋势，并在此基础上对各类保温措施对可靠度的提升效果进行研究，以保障无砟轨道在寒区环境下的长期稳定运营。

3、无砟轨道温度场受太阳辐射、风速、气温等多种气象因素共同影响，而各类保温材料可通过较低的导热系数或反射太阳辐射的能力有效阻止内外热量传递，保持结构温度稳定。针对保温措施对结构温度场稳定性的改善效果，有学者认为保温措施可显著保持混凝土内部温度稳定，明显改善其抗裂性能；有学者研究了聚苯乙烯及挤塑聚苯乙烯(xps)泡沫塑料在铁路下部结构中的保温作用，结果表明保温材料可有效降低路基冻胀对铁路结构变形的影响；有学者采用在轨道表面覆盖道砟层作为寒区无砟轨道保温措施，结果表明道砟层保温措施可有效降低外界温度变化引起的结构温度波动，减缓降温速率。

4、而针对不同荷载作用下的轨道结构承载能力可靠度，许多学者进行了研究，有学者通过假定荷载、抗力参数均值及变异系数，构造结构功能函数，利用一次二阶矩法对无砟轨道板抗弯可靠度进行了分析；有学者结合多重叠合梁模型建立了列车荷载作用下的轨道板横、纵向开裂失效的功能函数，并基于蒙特卡洛法对多种失效模式下结构可靠度进行了求解；有学者设置板式无砟轨道层间截面初始损伤，考虑损伤长度、高度、轨垫刚度及弹模的随机性，采用响应面法分析了结构可靠度。上述研究分析了轨道结构不同失效模式下的可靠度，但仅针对当前状态，未考虑时间变量，事实上荷载效应及结构抗力均为与时间相关的随机过程，需考虑时间变量对结构时变可靠度进行分析以清晰掌握结构服役状态，有学者考虑实际运营期间结构抗力衰减情况，采用高阶矩法对列车和温度荷载共同作用下的轨道板进行了抗弯、抗裂时变可靠度分析；有学者采用二次四阶矩法，分析了板式无砟轨道层间损伤的时变可靠度，并进一步分析了窄接缝初始损伤、温度荷载等对层间损伤时变可靠度的敏感度；有学者利用有限元法建立了列车及温度荷载耦合作用下的crtsⅲ型轨道板横向抗弯功能函数，考虑结构抗力退化，以直接概率积分法分析了其横向抗弯时变可靠度；有学者针对桥上无砟轨道底座板，考虑列车荷载、温度梯度与桥梁挠曲共同作用，利用一阶可靠性方法(first orderreliability method，简称form)将时变问题转换为时不变问题，以此计算了底座板的疲劳时变可靠度；有学者通过对时间变量进行离散，避免随机过程的复杂求解问题，将时变问题向时不变问题转化，以蒙特卡洛重要抽样法计算了结构时变可靠度。

5、在荷载不断作用及结构抗力逐渐退化下，轨道结构可靠度在设计年限内有较大风险低于限值，而目前针对结构可靠度的提升方法基本集中于结构抗力提高上，从初始设计或后期维护角度保持结构抗力在一个较为安全的水平，缺少通过降低结构荷载效应以提升可靠度的相关研究。另外，目前的研究在分析轨道结构可靠度及提升方法方面存在以下几点不足：

6、1)大多将随机变量考虑为经验值，通过假定荷载均值、变异系数和分布构建随机变量，与实际情况存在差异；

7、2)目前可靠度提升方法主要从提高结构自身抗力角度，缺少以降低荷载效应手段提升结构可靠度的研究。

技术实现思路

1、本发明的内容是提供一种不同保温隔热措施下寒区无砟轨道板时变可靠度分析方法，其能够克服现有技术的某种或某些缺陷。

2、根据本发明的不同保温隔热措施下寒区无砟轨道板时变可靠度分析方法，其包括以下步骤：

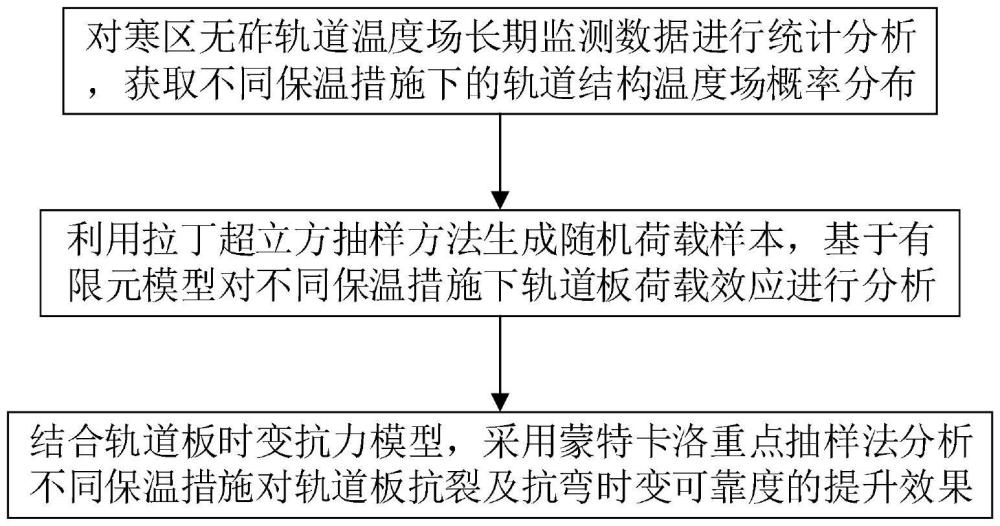
3、一、对寒区无砟轨道温度场长期监测数据进行统计分析，获取不同保温措施下的轨道结构温度场概率分布；

4、二、利用拉丁超立方抽样方法生成随机荷载样本，基于有限元模型对不同保温措施下轨道板荷载效应进行了分析；

5、三、结合轨道板时变抗力模型，采用蒙特卡洛重点抽样法分析了不同保温措施下轨道板抗裂及抗弯时变可靠度。

6、作为优选，步骤一中，对试验浇筑模型进行长期监测，试验浇筑模型为crtsⅲ型板式无砟轨道实尺模型，从上至下分别为承轨槽、c60预制轨道板、c40自密实混凝土、c40底座板；轨道结构横向中心处从轨道板顶面至底座板中心位置共设置七个测点，分别设置为轨道板顶面z1，距轨道板1/4位置z2，轨道板中部z3，轨道板与自密实混凝土交界处z4，自密实混凝土层中部z5，自密实混凝土层底部z6，底座板中部z7，通过七个温度测点位置，掌握轨道结构内部温度分布规律。

7、作为优选，步骤一中，选取多日内轨道板及自密实混凝土层温差数据，绘制轨道结构最大正温差频数分布直方图、轨道结构最大负温差频数分布直方图及对应的weibull分布拟合曲线，并进行分析。

8、作为优选，步骤二中，拉丁超立方抽样方法的过程如下：假定随机变量数量为k，p为n×k的矩阵，每列是由1～n的各不相同的随机整数，矩阵r是n×k的矩阵，r中的列元素是由0～1的均匀随机数组成，其中n为选取的样本组数，则采样矩阵s为：

9、

10、采样矩阵包含从0到1的随机数值，这些值均匀分布在累积分布函数的分层区域中；sij是矩阵s的第i行第j列元素，则：

11、

12、式中：是通过拉丁超立方抽样得到的样本中的第i组样本的第j个变量，是采样矩阵s的第j个变量所符合的分布函数；

13、通过上述步骤可对多组随机变量进行分层抽样，生成随机荷载样本。

14、作为优选，步骤二中，基于列车荷载及正温度、负温度梯度随机变量样本，输入有限元模型中批量计算，每组样本下提取轨道板各项荷载效应最大值，绘制频数分布直方图对轨道板荷载效应进行分析。

15、作为优选，蒙特卡洛重点抽样法为：

16、设x＝(x1,x2,···x1)为结构随机变量，其联合概率密度为fx(x)＝fx(x1,x2...xn)，结构功能函数z＝g(x)，则失效概率pf写为失效域示性函数的数学期望值：

17、

18、式中：rn为n维向量空间；为随机变量组合的n维向量(x1,x2...xn)t；为失效域示性函数，表示为：

19、

20、根据大数定律，失效域示性函数的样本均值近似表示失效域示性函数的期望值，即表示pf为：

21、

22、此时通过构造重要抽样函数，将抽取的样本分布重心控制在失效域附近，减少上式中的抽样次数；对于抽样重心的选取，目前选择功能函数的设计验算点，以此为中心构造重要抽样函数，设重要抽样密度函数为hy(·)，则失效概率pf转化为：

23、

24、依照上式进行样本的n次抽取之后，获取n个样本向量则得到pf近似值为：

25、

26、作为优选，时变可靠度分析方法为：

27、功能函数z为：

28、z＝g(r,s)＝r-s

29、式中：r为结构抗力；s为结构荷载效应，即作用在结构上的各种荷载引起的变形、位移；

30、无砟轨道在设计年限内结构可靠度会随服役时间t而不断变化，故结构功能函数z需考虑为与时间相关的随机过程，此时将上式改写为：

31、z(t)＝g(r(t),s(t))＝r(t)-s(t)

32、式中：t为时间变量；r(t)为时变抗力；s(t)为时变荷载效应；

33、设运营年份为t，将时变荷载效应分布s(t)，考虑为[0,t]内的最大值，时变抗力分布r(t)考虑为[0,t]内的最小值，此时上式转化为：

34、

35、将非平稳随机过程平稳化，故得到运营t年时荷载效应最大值分布函数为

36、ft(x)＝[f(x)]n

37、式中f(x)为日荷载效应分布函数；n为运营t年内有效作用天数n＝d×t，其中d为一年内荷载作用有效天数。

38、本发明通过开展寒区无砟轨道温度场监测试验，获取不同保温隔热措施下轨道结构温度场概率分布，利用随机抽样方法生成随机荷载样本，基于有限元模型分析了不同保温隔热措施对轨道板荷载效应的削弱效果，考虑了保温材料对温度的梯度的削弱效果，并结合结构抗力退化模型建立了轨道板抗裂及抗弯时变功能函数，分析了不同保温隔热措施下轨道板抗裂及抗弯时变可靠度，以期对寒区环境下无砟轨道长期安全运营及维护提供一定参考。