一种单输入安全多方计算协议的构造方法

本发明属于安全多方计算领域的一种单输入安全多方计算协议，具体涉及了一种面向非诚实大多数模型的单输入安全多方计算协议构造方法。

背景技术：

1、安全多方计算作为一种隐私计算方法，允许互不信任的参与方们共同计算出一个公共函数的结果，在此过程中不泄露参与方们的秘密输入。单输入安全多方计算作为一种特殊的安全多方计算，只有一个特殊的参与方（被称为证明者）拥有秘密输入，而其他参与方（被称为验证者）没有秘密输入。单输入安全多方计算允许证明者利用自己的秘密输入计算一个公共函数的结果，而验证者们可以验证计算结果是否正确，并且在此过程中不泄露证明者的秘密输入。

2、单输入安全多方计算有着许多应用场景，比如零知识证明、可验证秘密分享、隐私聚合系统等。在国际知名的隐私聚合系统prio中，服务器集群以隐私保护的方式收集并聚合客户端的数据，客户端可以用单输入安全多方计算来向服务器集群证明自己的数据是有效的，同时服务器集群可以验证客户端数据的有效性。

3、目前阶段，单输入安全多方计算的研究工作主要集中于诚实大多数模型，即敌手只能控制小于半数的参与方。

4、文献1，benny applebaum, eliran kachlon, and arpita patra. verifiablerelation sharing and multi-verifier zero-knowledge in two rounds: tradingnizks with honest majority. crypto 2022。其提供了一种基于诚实大多数模型的单输入安全多方计算的构造方法，该方法的在线阶段也仅需一轮，但是其仅具备理论可行性，该方法的实际性能较差，难以用于生产实践。

5、文献2，kang yang and xiao wang. non-interactive zero-knowledge proofsto multiple verifiers. asiacrypt 2022。其提出了一种基于诚实大多数模型的多验证者零知识证明方法，该方法可以被看作是一种特殊的单输入安全多方计算。该方法在线阶段仅需两轮通信，并且非常高效。然而该方法不能直接拓展到单输入安全多方计算，同时该方法基于诚实大多数模型，而不是非诚实大多数模型。

6、文献3，carsten baum, robin jadoul, emmanuela orsini, peter scholl, andnigel p. smart. feta: efficient threshold designated-verifier zero-knowledgeproofs. acm ccs 2022。其提出了一种基于诚实大多数模型的多验证零知识证明方法，该方法也可以被看作是一种特殊的单输入安全多方计算。该方法提供了代码实现，性能非常高，可以被用于生产实践。然而，该方法无法拓展到非诚实大多数模型。

7、文献4，zhelei zhou, bingsheng zhang, hong-sheng zhou, and kui ren.practical constructions for single input functionality against a dishonestmajority. ieee euro s&p 2024. 其提出了一种基于非诚实大多数模型的单输入安全多方计算的构造方法，并且提供了代码实现，其性能优秀，然而该方法的离线阶段较为耗时，并且在线阶段的通信轮数高于两轮，有较大的优化空间。

8、文献5，matt lepinski, silvio micali, and abhi shelat. 2005. fair-zeroknowledge. tcc 2005。其提出了一种基于非诚实大多数模型的多验证者零知识证明方案，该方法可以被看作是一种特殊的单输入安全多方计算。然而该方法不能直接拓展到单输入安全多方计算，而且该方法仅具备理论可行性，实际性能很差，无法用于生产实践。

技术实现思路

1、为了解决背景技术中的需求和问题，本发明提供了一种面向非诚实大多数模型（敌手可以控制超过半数的参与方）的常数轮的单输入安全多方计算协议构造方法，本发明在线阶段仅需一轮通信。

2、本发明的技术方案如下：

3、一、一种单输入安全多方计算协议的构造方法

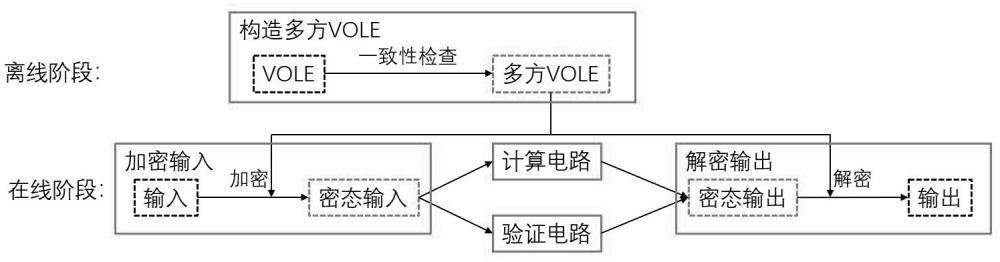
4、构造多方vole协议，获取证明者的安全输入消息、 m个安全输入解密密钥以及 m个验证者对应的全局密钥、安全密态输出；

5、利用证明者的安全输入消息、 m个安全输入解密密钥以及 m个验证者对应的全局密钥、安全密态输出对每个验证者的输入进行加密，获得 m个验证者的密态输入消息；

6、将 m个验证者的密态输入消息输入到电路拓扑结构中， m个验证者获得密态输出消息；

7、证明者对验证者获得的密态输出消息进行解密后，使得各验证者获得正确输出消息。

8、所述构造多方vole协议，获取证明者的安全输入消息、 m个安全输入解密密钥以及 m个验证者对应的全局密钥、安全密态输出，包括：

9、对于1个证明者和 m个验证者，证明者与每个验证者都执行一次两方vole协议，并且证明者每次执行两方vole协议时的原始输入消息均相同，每个验证者对证明者的原始输入消息进行一致性检查并验证通过后，则构造多方vole协议构造完成，输出证明者的安全输入消息、 m个安全输入解密密钥以及 m个验证者对应的全局密钥、安全密态输出。

10、所述每个验证者对证明者的原始输入消息进行一致性检查并验证通过，包括：

11、所有参与方共同采样出一个有限域f p上的长度为 n的随机向量 s，记为一致性生成消息，证明者计算一致性生成消息和原始输入消息的内积并记为输入检查消息，以及一致性生成消息和第 i个验证者的原始输入解密密钥的内积并记为解密密钥检查消息；随后证明者将输入检查消息和解密密钥检查消息发送给第 i个验证者，第 i个验证者收到后计算一致性生成消息和原始密态输出 w ( i)的内积并记为一致性验证消息，然后基于输入检查消息、全局密钥、解密密钥检查消息和一致性验证消息验证进行验证。

12、所述证明者的安全输入消息、 m个安全输入解密密钥分别为证明者的原始输入消息 u的前 n-1位分量，以及 m个原始输入解密密钥 v ( 1 ),…, v ( m )的前 n- k位分量，第 i个验证者的全局密钥、安全密态输出分别为其全局密钥的前 n- k位分量、原始密态输出的前 n- k位分量。

13、所述利用证明者的安全输入消息、 m个安全输入解密密钥以及 m个验证者对应的全局密钥、安全密态输出对每个验证者的输入进行加密，获得 m个验证者的密态输入消息，包括：

14、对于第 i个验证者，根据证明者的明文长度对安全输入消息进行截取，获得加密输入消息 u in，证明者计算其明文与加密输入消息 u in的差值后获得加密消息θ，第 i个验证者根据证明者的明文长度对安全密态输出进行截取，获得加密密态输出 w in ( i )，第 i个验证者根据加密消息θ对加密密态输出 w in ( i )进行更新，获得最终的加密密态输出 w in ( i )。

15、对于所述电路拓扑结构中的第 j个乘法门，其两个输入导线的明文分别是 x α, j , x β , j，证明者所持有的两个解密密钥分别为 v α , j ( j ), v β , j ( j )， i∈[ m]，第 i个验证者所持有的两个输入导线的密态值分别为 w α , j ( i ), w β , j ( i )，截取安全输入消息、第 i个安全输入解密密钥的第 n+ j位分量并分别记为乘法输入消息乘法 u× , j、乘法输入解密密钥 v ( i )× ,  j，第 i个验证者截取安全密态输出的 n+ j位分量并记为乘法密态输出 w ( i )× ,  j；

16、证明者本地计算输出导线的明文 x γ, j和相对应的解密密钥 v γ , j ( i )，公式分别为 x γ , j = x α , j · x β , j  mod  p， v γ , j ( i )= v ( i )× , j  mod  p，然后证明者根据输出导线的明文 x γ, j和乘法输入消息乘法 u×, j的差值计算获得辅助计算消息 d j并发送给所有验证者；第 i个验证者本地更新乘法密态输出并作为输出导线的密态值。

17、所有验证者对所述电路拓扑结构进行乘法门电路验证，包括：

18、对于所述电路拓扑结构中的第 j个乘法门以及第 i个验证者，截取证明者的安全输入消息、第 i个安全输入解密密钥的前 n1+ n2+1位分量， n1为证明者的明文长度， n2为乘法门数量，分别记为初始乘法验证消息 u×, n2+1，乘法验证解密密钥 v ( i)×, n2+1，第 i个验证者截取其安全密态输出的前 n1+ n2+1位分量并记为乘法验证密态输出 w( i)×,  n2+1；证明者先用哈希函数 hash来计算生成一个随机数 r  j并记为乘法验证随机数，基于乘法验证随机数计算获得乘法验证聚合消息 u和乘法验证解密聚合密钥 v ( i)并发送给第 i个验证者，第 i个验证者基于乘法验证聚合消息 u和乘法验证解密聚合密钥 v ( i)计算获得乘法验证密态聚合输出 w ( i)并进行验证。

19、二、一种安全多方计算方法

20、所述安全多方计算方法利用所述的一种单输入安全多方计算协议的构造方法进行安全多方计算。

21、三、一种计算机设备

22、所述设备包括存储器和处理器，所述存储器存储有计算机程序，所述处理器执行所述计算机程序时实现所述方法的步骤。

23、四、一种计算机可读存储介质

24、所述介质上存储有计算机程序，所述计算机程序被处理器执行时实现所述方法的步骤。

25、本发明的有益效果为：

26、本发明解决了诚实大多数模型的限制，构造了多方vole协议，并基于此对输入输出进行加解密操作，保障了协议的隐私性，有更高的安全性。

27、本发明不仅不需要诚实大多数的假设，有更高的安全性，同时拓宽了协议的应用范围。本发明提出了一种新型的乘法门验证协议，降低了在线通信轮数，即仅需一轮在线通信，达到了在线阶段通信轮数最优。