计及按需自治移动系统的交通网-配电网耦合系统定价机制

本发明涉及配电网运行分析领域，具体是一种计及按需自治移动系统(amods)的交通网-配电网耦合运行系统定价机制。

背景技术：

1、交通网中电动汽车的占比逐年提高，配电网的供电负荷加重，与城市交通网的耦合关系日渐增强。一方面，路况、用户出行需求、路网结构等交通特性会影响用户的充电行为，从而影响电网的运行；另一方面，电网中充电设施的布局、充电价格等因素也会影响用户的充电决策和路径选择，从而影响交通网络的流量分布。合理的定价策略可以激励ev用户有序充放电，是调节电动汽车负载的有效方法，但目前已有的研究很少从用户的角度出发，导致收取费用过高，难以满足用户心理预期，无法在实践中执行；随着自动驾驶技术的快速发展，按需自治移动系统(autonomous mobility on demand,amod)成为一种具有前景的出行模式，也为电力-交通网的协调调度提供新的思路，然而，目前研究未充分考虑amod系统中的自动驾驶ev、传统用户自发决策ev与燃油车(gasoline vehicle,gv)共同存在的复杂交通流与配电网的耦合关系。

技术实现思路

1、本发明针对现有传统交通网-配电网耦合系统定价方法很少从用户的角度出发，导致收取费用过高，难以在实践中执行，且现有分析方法难以适用于含无人驾驶车辆的交通网-配电网耦合运行分析的不足，提出了计及按需自治移动系统的交通网-配电网耦合系统定价机制，以降低耦合系统运行成本同时最小化对用户的额外收费为目标，为优化城市交通-电力耦合网络的运行提供参考。接入amod系统，构建配电网和复杂交通流的双层耦合模型，通过上下层形式，分别刻画配电网-无人能驾驶车队系统合作运行模式与不可控车辆用户的随机用户均衡模式；为有效减少计算量并最小化额外收费，基于逆优化方法为不可控车流建立了最低收费定价模型。所收取的额外费用作为补贴给可控的自动驾驶ev以及电力-交通运营商。

2、为实现上述目的，本发明提供如下技术方案：

3、本发明涉及计及按需自治移动系统(amods)的交通网-配电网耦合系统定价机制。首先本发明接入amod系统，构建了含可控电动汽车与不可控燃油车、电动汽车的复杂交通流和配电网的双层耦合模型。其中采用基于logit的随机用户均衡(sue)模型描述交通网中不可控车辆用户的驾驶行为，并构建系统最优(so)模型来最小化配电网与可控ev的运营成本。其次，本发明基于逆优化方法为不可控车流建立了最低收费定价模型，以最小化额外用户费用，同时逆优化法能够有效减少计算量。所收取的额外费用作为补贴给可控的自动驾驶ev以及电力-交通运营商。

4、所述的交通网-配电网耦合运行分析是指：由交通网道路、车流信息和配电网源-荷、线路信息出发，分析交通网-配电网在交互均衡下的运行参数，包括配电网潮流状态变量(如节点电压参数、线路功率流等)和交通网的交通流状态变量(道路车流分布，路段通行时间等)。

5、所述的按需自治移动系统是指：该系统可以调度自动驾驶电动汽车高效响应交通网用户的出行需求，综合全局信息选择成本最优的路径，并综合未来出行需求量预测信息和道路拥堵情况、配网节点电量消纳压力等信息，规划当前自动驾驶电动汽车的选择性充电行为，协助优化配电网潮流。

6、所述的可控电动汽车是指：受按需自治移动系统统一调度的自动驾驶电动汽车，在满足用户出行订单的同时，通过电动汽车充电行为辅助配电网降低发电成本，消纳过剩可再生能源。

7、所述的不可控车流是指：由用户自发决策驾驶行为的车流。

8、所述的逆优化是指：给定一组决策，求使该决策成为最优决策的目标函数或约束的方法，在本发明中，首先得到能使配电网-无人驾驶车流成本最小，且不可控车流达到随机系统最优(sso)状态时的目标状态，然后求解能达使系统达到目标状态的定价机制。

9、所述的系统最优(so)是指：无人驾驶车辆调度平台和配电网运营商以协议形式达成合作，使二者的总体运行成本在可协调范围内最低。

10、所述的总体运行成本包括：交通网车辆路径通行时间，充电费用(如有充电需求)；配电网发电成本，自上级电网购电成本，新能源弃用惩罚成本。

11、所述的随机系统最优(sso)是指：不可控车流用户存在路况感知偏差的同时选择使总体不可控车流用户成本最低的路径。

12、所述的总体不可控车流用户成本包括：交通网车辆路径通行时间，充电费用(如有充电需求)。

13、所述的随机用户均衡(sue)是指：不可控车流用户均从自身利益出发，选择符合自身出行需求且在其认知情况下出行成本最低的路径，最终使整体车流达到的均衡状态。

14、本发明计及按需自治移动系统的交通网-配电网耦合系统定价机制，包括如下步骤：

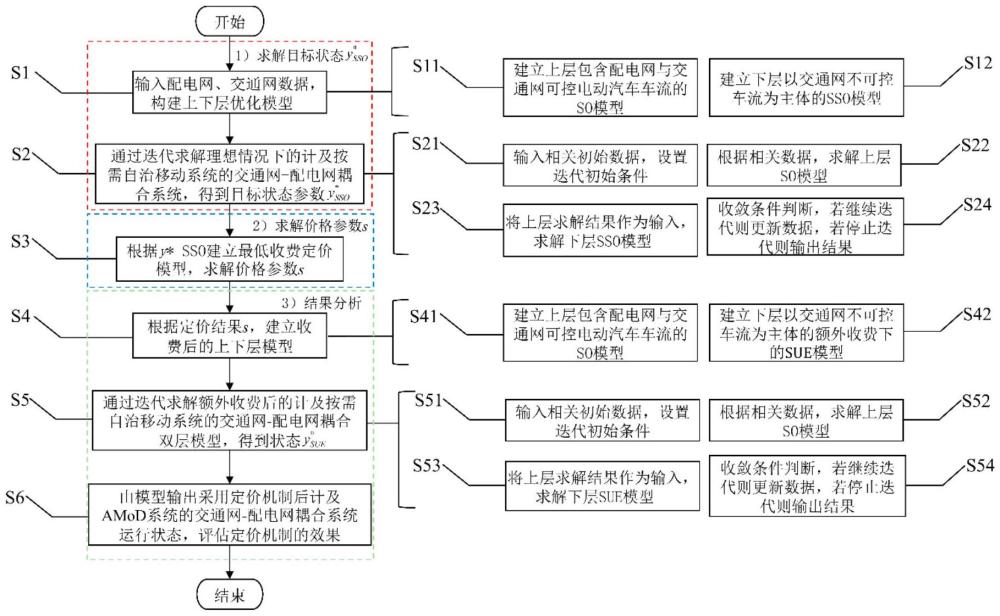
15、步骤s1：输入配电网、交通网数据，根据配电网源-荷、线路信息和交通网道路、车流信息，构建上下层优化模型，刻画理想情况下的计及amod系统的交通网-配电网耦合运行方式。该建模方式具体包括：

16、步骤s11：建立上层包含配电网与交通网可控电动汽车车流的so模型。amod系统综合全局信息对自动驾驶电动汽车进行统一调度，与配电网通过协议合作。

17、步骤s12：建立下层以交通网不可控车流为主体的sso模型。配电网运营商根据潮流状态，以对应充电站节点的节点边际电价作为普通电动汽车用户的充电电价；理想情况是驾驶员根据其认知，选择使总体不可控车流用户成本最低的路径实现出行需求并进行充电，考虑到用户对路况的认知偏差，设计用户随机性系统最优模型刻画不可控车流用户驾驶行为。

18、步骤s2：输入初始数据，通过迭代求解理想情况下的计及按需自治移动系统的交通网-配电网耦合系统，得到目标状态

19、步骤s21：输入相关初始数据，设置迭代初始条件(包括收敛阈值与最大允许迭代次数)

20、步骤s22：根据相关数据，求解上层so模型。

21、步骤s23：将上层求解结果作为输入，求解下层sso模型。

22、步骤s24：判断是否达到收敛条件：若达到收敛条件则停止迭代，得到理想状态下的状态若未达到收敛条件，将下层求解结果更新为上层so模型的输入，继续步骤s22。

23、步骤s3：根据建立最低收费定价模型，保持收费后模型中的车流分布与理想状态的sso模型中的车流分布一致，价格参数s成为优化变量进行求解。求解该模型得到交通拥堵费与充电附加费的定价结果s。

24、步骤s4：输入配电网、交通网数据，建立根据定价结果s进行收费后的上下层模型，刻画额外收费后的计及amod系统的交通网-配电网耦合运行方式。该建模方式具体包括：

25、步骤s41：建立上层包含配电网与交通网可控电动汽车车流的so模型，该模型与s11中的上层so模型相同。

26、步骤s42：建立下层以交通网不可控车流为主体的额外收费下的sue模型。在该模型中采用步骤s3中得到的定价结果对不可控车流用户进行收费。现实情况中驾驶员会根据其认知，选择使自身出行成本最低的路径实现出行需求并进行充电，因此考虑到用户对路况的认知偏差，设计随机用户均衡模型刻画不可控车流用户驾驶行为。

27、步骤s5：将得到的价格s代回收费后的交通网-配电网耦合双层模型中，此时上层为so模型，下层为收取额外费用的sue双层模型，通过迭代求解额外收费后的计及按需自治移动系统的交通网-配电网耦合双层模型，得到状态

28、步骤s51：输入相关初始数据，设置迭代初始条件(包括收敛阈值与最大允许迭代次数)。

29、步骤s52：根据相关数据，求解上层so模型。

30、步骤s53：将上层求解结果作为输入，求解下层sue模型。

31、步骤s54：判断是否达到收敛条件：若达到收敛条件则停止迭代，得到额外收费后的系统状态若未达到收敛条件，将下层求解结果更新为上层so模型的输入，继续步骤s52。

32、步骤s6：迭代结束后，判断是否与一致，若一致，则验证了求解过程的正确性；并根据采用定价机制后计及amod系统的交通网-配电网耦合系统运行状态，可以计算采用定价机制后系统的成本，对定价机制的效果进行评估。

33、所述步骤s11中所述的上层so模型，目标函数为：fpdn为配电网的运营成本，futn为可控车流的总成本。其中：w为出行时间成本的转化系数；mi、ni为发电成本系数；λ为配电网购电的成本系数；γ为rdg弃电成本系数；与为节点i电源的有功和无功注入功率；与为节点i与节点j之间线路的有功和无功传输功率；与为分布式可再生能源接入节点i的有功与无功功率；为道路可控车流，为道路不可控车流；ta为道路通行时间，随道路上的车流量变化，表达式为：为充电站a的充电电价，该充电站连接到pdn的总线j；ec为电动汽车充电的电量。

34、所述的上层so优化问题的约束条件，具体包括：交通网侧的约束条件和配电网侧的约束条件。其中交通网侧约束条件表达式为：

35、

36、为可控电动汽车在o-d对rs之间的出行需求基准量；为可控汽车在o-d对rs之间路径k上的车流量；为可控汽车在o-d对rs之间路径k与道路a的关联系数，当路径k包括道路a时，为1，否则为0。式(1)为可控交通流守恒约束；式(2)表示可控ev链路流量与路径流量的关系。

37、配电网侧约束条件表达式为：

38、

39、rij与xij分别为线路ij的电阻与电导值；iij为线路ij上的电流，imax为线路上能承受的最大电流值；ui为节点i的电压幅值，umax与umin分别为节点i电压幅值的上下限；pmin、pmax和qmin、qmax分别为节点i有功、无功注入功率的上下限；分别为总线j处的有功、无功功率需求，为传统负载需求，为电动汽车充电需求；

40、式(3)为配电网的运营成本fpdn的表达式，第一项表示传统发电成本，第二项为公用电网的购电成本，第三项为rdg弃电的惩罚成本。式(4)为可控车流成本futn的表达式，分别为可控ev的总时间成本与总充电成本两项。式(5)、式(6)分别表示有功与无功平衡约束；式(7)表示pdn线路的电压降落；式(8)表示传输功率限制；式(9)、式(10)分别表示线路电流、电压以及有功、无功发电的限制；式(11)表示总线j处的有功功率需求包括传统负载需求和电动汽车充电需求，电动汽车充电需求为连接到pdn总线j的充电站a上的车流量与每辆车充电量的乘积。式(12)表示缩减rdg的有功功率可以平衡pdn操作。

41、所述步骤s12中的下层考虑用户选择路径随机性的sso模型指：以gumbel分布刻画用户认知偏差项，得到用户出行选择概率的模型。该模型下，某出行用户选择路径i的概率为：

42、

43、式中，θ(θ≥0)为不可控车辆用户对出行成本的感知系数，该系数与用户路况感知的偏差程度成反比，即θ越大，用户的感知偏差程度越轻，有更大的概率选择到使自身出行成本最小的路径。为用户均衡状态下在o-d对rs路径k上的出行成本。

44、所述下层sso模型的目标函数为：其中：包括下层不可控车流的总出行时间成本、不可控电动汽车的充电成本与表示用户选择随机性的项。为不可控车流的总出行成本；为下层不可控车辆的链路流量，与分别表示不可控燃油车与电动汽车在o-d对rs之间路径k上的车流量。

45、所述的下层sso优化问题的约束条件有：

46、

47、

48、与分别为不可控燃油车与电动汽车在o-d对rs之间的出行需求基准量；分别为不可控燃油车与电动汽车在o-d对rs之间路径k与道路a的关联系数，当路径k包括道路a时为1，否则为0；为下层不可控燃油车的链路流量，为下层不可控电动汽车的链路流量。

49、式(11)为不可控交通流守恒约束；式(12)分别表示不可控gv与ev链路流量与路径流量的关系；式(13)表示下层链路流量为不可控gv与ev链路流量的和。

50、所述步骤s22中上层so模型计算所需的相关初始数据包括初始电动汽车在各充电站充电量与下层不可控车流分布

51、所述步骤s23中下层sso模型计算所需的上层so模型求解结果包括可控车流分布与更新后的充电站节点电价

52、所述步骤s24中最终目标状态包括上层道路流量下层道路流量以及电价

53、所述步骤s3中的价格参数s包括道路拥堵费τa与充电附加费σa。

54、所述步骤s3中的最低收费定价模型，可以使向用户收取的额外费用最小。目标函数为：包括向不可控车流收取的道路拥堵费与充电附加费两项。当用户自发选择出行路径时，并不会以系统最优为目标，而是以自身成本最小为目标，因此将向不可控车流收取交通拥堵费与充电附加费的sue模型转换为约束，刻画用户自主驾驶行为。最低收费定价模型的约束条件有：

55、sso-cons(11)-(13)

56、

57、

58、其中，以及λ*均为中的已知量。式(16)、式(17)分别为道路拥堵费与充电附加费的上下限约束；式(18)-(22)为代入理想状态参数后收取额外费用后的sue状态的kkt条件，基于互补松弛约束(20)，在考虑用户随机性的情况下，如果不可控gv的路径流量则若则因此，o-d对中每位gv用户所行驶的路径成本均相同且最小，同理不可控ev用户亦是如此。

59、所述步骤s41中的上层so模型与步骤s11中的so模型相同。

60、所述步骤s42中的下层为收取额外费用的sue模型，目标函数为：其中：约束条件与步骤s12中sso模型的约束相同。在该模型中，交通拥堵费τa与充电附加费σa即为步骤3中求得的价格信号s。

61、所述步骤s5中将收费后的双层模型进行迭代，求解得到此时的上下层的交通流分布与各充电站节点电价，即对不可控车流进行额外收费后的耦合模型状态

62、与现有技术相比，本发明的有益效果是：本发明建立接入amod系统的交通网-配电网耦合系统模型，提出了基于随机用户均衡的交通网优化问题与配电网最优潮流问题，amod系统将自动驾驶电动汽车引入交通网，通过与配电网合作，改进传统的交通网-配电网耦合模式，使耦合系统的运行状态精细化，通过额外收费对交通网-配电网耦合系统进行协调优化，并基于逆优化方法建立最低收费定价模型，显著降低计算复杂度，使收费后自发形成的不可控交通流分配与成本最低的sso状态一致，同时使向用户收取的额外费用最小。与现有技术相比，本发明弥补了现有传统交通网-配电网耦合系统定价方法很少从用户的角度出发，导致收取费用过高，难以在实践中执行，且现有分析方法难以适用于含无人驾驶车辆的交通网-配电网耦合运行分析的不足，提出了计及按需自治移动系统的交通网-配电网耦合系统定价机制，以降低耦合系统运行成本同时最小化对用户的额外收费为目标，为优化城市交通-电力耦合网络的运行提供参考。