基于主题感知的最具影响力社区在线搜索方法、系统及计算机可读存储介质

本发明涉及社区搜索，尤其涉及基于主题感知与影响力融合的社区搜索方法。

背景技术：

1、随着在线社交网络(如facebook、x、微博等)的迅速发展，大型图已被广泛用于数据分析，并且人们对于在其中获取有用信息的需求日益增长。在这些大型图中，社区(community)是一个重要组成部分，它通常被定义为图中一小群紧密连接的顶点所形成的内聚子图。而从图中寻找社区的工作被称为社区搜索(community search，cs)，它是大数据分析中的一个基本问题，并且已经广泛应用于广告投放、社交推荐、事件组织等领域当中。近年来，研究人员开始将社会影响力纳入至社区搜索问题中，旨在找到一组不仅紧密相连，且具有高度影响力的顶点，或者是将主题纳入至社区搜索问题当中，找到一组连接紧密、主题关联的顶点。尽管研究人员对这两类问题进行了广泛研究，但只有少数尝试将社会影响力和主题同时纳入至cs问题当中，并且仅有的一些关于影响力和主题感知结合的cs问题的研究仍然存在一些局限性：

2、1)内聚性定义单调

3、在内聚性的定义中，现有技术采用了经典的k-core和k-truss模型及其变体。但这些模型不能表示不同主题上用户之间关系的强度，因为它们只考虑两个顶点之间是否存在边(即连接)。

4、2)没有考虑更贴近实际的不确定图场景

5、它们并没有捕捉到社区形成的不确定性，因为它们的定义都是基于确定性图的，即边生成概率一定为1。

6、3)没有考虑不同主题下的影响力变化

7、在影响力方面，大多数工作预先为每个顶点指定一个固定的影响力分数。这样的方案并没有反映出用户的影响力随着主题的变化而变化，并且信息在社交网络中的传播通常由随机扩散模型来描述，如独立级联(ic)模型。

8、以上这些限制会阻碍现有cs方法在现实场景中的应用。

技术实现思路

1、本发明的目的是针对现有技术的不足而提供的一种基于主题感知的最具影响力社区在线搜索方法。该方法是为解决在更为复杂的社交网络图下，搜索到一个潜在社区，该社区同时满足与查询主题的高度关联、给定主题下最高的对外影响力、社区内极高的内聚度等三个特征。

2、实现本发明目的的具体技术方案是：

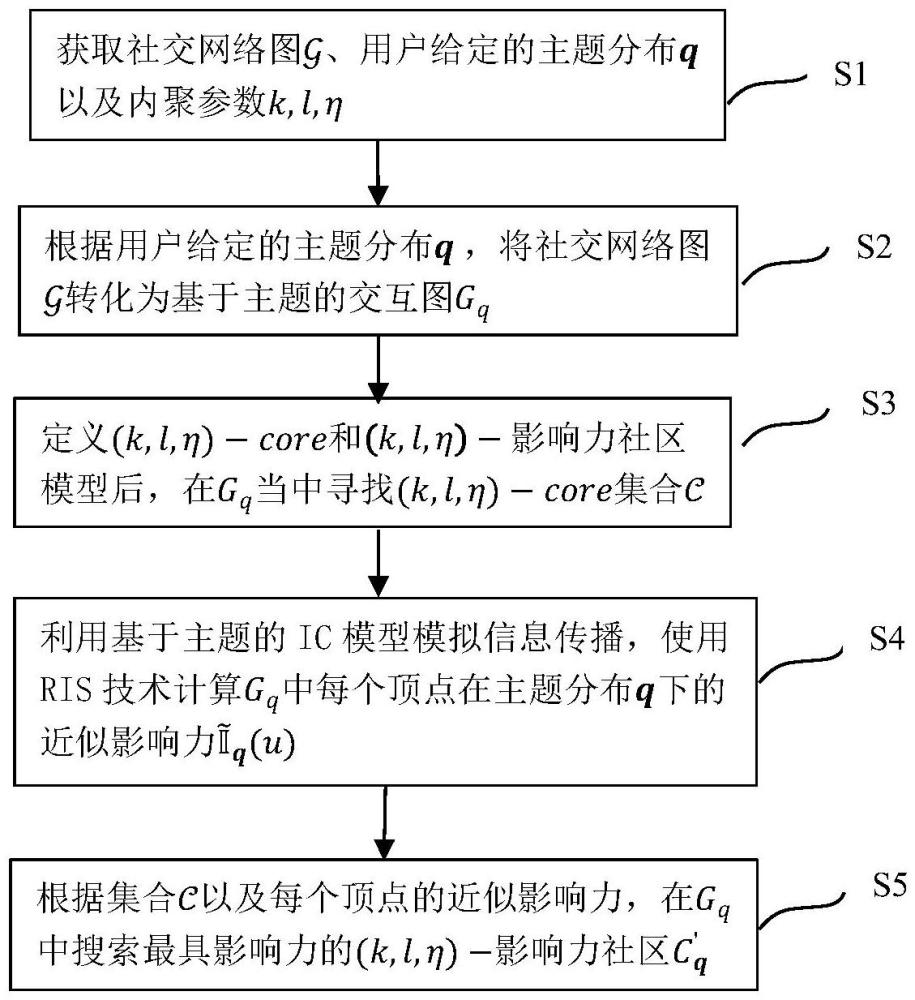
3、步骤1：获取社交网络图用户给定的查询主题分布q以及内聚参数k,l,η。

4、该社交网络图中的每个顶点代表一个用户实体，每条有向边e∈ε上拥有主题分布，表示两个用户实体之间在不同主题下的社交关系权重，即ω(e)＝(ω1(e),...,ωz(e))，e＝(u,v)∈ε，其中z表示主题数量，ωi(e)表示用户u对用户v在第i个主题上的关系权重。而本发明的目的便是在这样一个复杂的社交网络中根据用户给定的查询主题q以及用户希望的内聚程度搜索到对应的潜在社区。

5、步骤2：根据用户给定的主题分布q，将社交网络图转化为基于主题分布q的交互图gq＝(vq,eq,p)。

6、基于主题的交互图gq＝(vq,eq,p)是从步骤1给定的社交网络图中提取的与向量q相关的一个有向不确定图，其中p是将每条边e∈ε映射到[0,1]区间内的概率值p(e)的集合。具体来说，这个概率值由社交网络图中每条边的主题分布与用户给定的主题分布q运算得来，即p(e)＝f(<ω(e),q>)，其中<,>表示两个向量的点积，而f(·)是一个单调函数，用于将任意非负实数归一化到范围[0,1]区间内。相应地，eq＝{e∈ε∣p(e)>0}，vq＝{u∣(u,v)∈eq}∪{v∣(u,v)∈eq}。

7、步骤3：定义并提供一种有向不确定图密度指标(k,l,η)-core和一种社区模型(k,l,η)-影响力社区。

8、步骤3-1：(k,l,η)-core是一个在k-core之上扩展的结构凝聚力评估指标，它适用于有向不确定图，也是本发明之一。具体来说，它是用来提取步骤2中交互图gq＝(vq,eq,p)的内聚子图，一个(k,l,η)-core是一个满足的极大诱导子图c＝(vc,ec,p)，其中表示顶点v在图c中的入度，而表示顶点v在图c中的出度。此外，由于假设每条边的存在都是独立的，因此可以等价于与的乘积。

9、步骤3-2：(k,l,η)-影响力社区是本发明要搜索的潜在社区的模型，它更加契合于有向不确定图。每个(k,l,η)-影响力社区c'都有对应的社区影响力分数它表明了不同社区在步骤1中给定主题q下的影响力，而的影响力分数定义为c'内顶点影响力最小值，即此外，一个(k,l,η)-影响力社区c'需要满足三个特性：1)弱连通特性；2)内聚性，即c'是步骤2中交互图gq的一个(k,l,η)-core；3)极大性，即不存在其他诱导子图c”满足前两个特性并包含c'的同时，也满足

10、步骤4：从gq中搜索多个极大(k,l,η)-core并存入集合包括以下子步骤：

11、步骤4-1：为了找到满足(k,l,η)-core的子图，第一步是计算gq中每个顶点v的和概率，它们的具体计算方法采用了bonchi等人提出的动态规划方法。

12、步骤4-2：判断当前gq中是否还存在某个顶点v不满足(k,l,η)-core的条件，即如果是则执行步骤4-3，否则执行步骤4-5。

13、步骤4-3：删除与顶点v相邻的所有入边e＝(u,v)，并更新指向v的邻居顶点u的出度满足≥l的概率，即类似地，还需要删除与顶点v相邻的所有出边e＝(v,u)，更新v作为起点所指向的邻居顶点u的入度满足≥k的概率，即

14、步骤4-4：从gq当中删除顶点v。

15、步骤4-5：重复上述步骤4-1至步骤4-4，直到gq中每个顶点v∈vq都满足当每个顶点都满足后，此时的gq可以被视为一个全局的(k,l,η)-core。但由于它不能保证连通，因此还需要将gq当中所有弱连通子图(即局部(k,l,η)-core)c插入到集合当中。

16、步骤5：利用基于主题的ic模型模拟信息传播，并使用ris技术计算gq中每个顶点在主题分布q下的近似影响力包括以下子步骤：

17、步骤5-1：从gq当中采样θ个子图g'1,…,g'θ，并对每个顶点u∈vq计算θ个rr集合rr(u,g'1),…,rr(u,g'θ)。其中采样子图g'i是通过在gq当中以概率1-pp(e)的概率随机去除每条边e∈eq而获得，并且pp(e)＝ap(e)，α∈(0,1]则是一个放缩因子，用来加速收敛。另外，rr集合也被称为反向可达集合，rr(u,g'i)意为在采样子图g'i中可以到达u的顶点集合；

18、步骤5-2：对于每个顶点u∈vq，获得每个采样子图中包含u的rr集合的平均数量作为其影响得分，即以此来计算所有顶点的近似影响力。此外，本发明还运用霍夫丁不等式给出了对该近似影响力结果的理论保证，即当时，对于每个顶点v∈vq有至少1-δ的概率保证

19、步骤6：在gq中搜索最具影响力的(k,l,η)-影响力社区c'q，包括以下子步骤：

20、步骤6-1：在得到每个顶点的近似影响力分数和(k,l,η)-core的集合后，创建一个大顶堆将集合当中的每个(k,l,η)-corec按照近似影响力的降序插入至中。

21、步骤6-2：初始化和前者用于存放目标社区，后者用于维护当前最大的近似影响力分数。

22、步骤6-3：判断是否为空，如果是则执行步骤6-3，否则跳转至6-8；

23、步骤6-4：取的堆顶(k,l,η)-corec，并将其从堆中移出；

24、步骤6-5：如果那么更新

25、步骤6-6：寻找当前c中近似影响力最低的顶点并将它从c中删除。

26、步骤6-7：首先删除与v*相连的邻边，并分别更新邻居顶点u的与随后继续判断当前c中是否还有不满足条的顶点，即如果有则继续删除，直到剩余顶点均满足(k,l,η)-core的特性为止。

27、步骤6-8：将c中余下的所有弱连通子图继续插入至大顶堆当中，因为某些顶点的删除，可能会导致c不满足连通性。

28、步骤6-9：重复上述步骤6-3至步骤6-8，直到大顶堆为空为止。最后返回维护后的c'q，即在主题q下满足最具影响力的潜在社区。

29、基于以上方法，本发明还提出了一种基于主题感知的最具影响力社区在线搜索系统，包括：存储器和处理器；所述存储器上存储有计算机程序，当所述计算机程序被所述处理器执行时，实现本发明上述的方法。

30、本发明还提出了一种计算机可读存储介质，其上存储有计算机程序，所述计算机程序被处理器执行时，实现本发明上述的方法。

31、总体而言，通过本发明所构思的以上技术方案与现有技术相比，能够取得下列有益效果：

32、1)该发明所考虑的是更为复杂的有向不确定图场景，相比于现有技术，它具有极大的挑战，并且由于现有技术中并没有适用于该图场景下的社区模型，本发明分别定义并提供了(k,l,η)-core以及(k,l,η)-影响力社区模型。

33、2)大多数基于影响力的cs方法简单地预先为每个顶点指定一个固定的影响力分数，而忽略了影响力随主题变化而变化的一个特性。本发明则通过利用扩散模型模拟图中顶点的影响力传播很好地解决了这个问题，但由于计算精确的影响力分数是一个#p难问题，本发明结合了速度更快的ris技术计算近似的影响力分数，并给出了结果的理论保证。