一种水润滑轴承界面摩擦振动噪声分析方法

本发明涉及水润滑轴承，具体涉及一种水润滑轴承界面摩擦振动噪声分析方法。

背景技术：

1、舰船推进装置环境恶劣且工况复杂多变，特别是低速、偏载和启停等服役工况下，水润滑橡胶轴承与轴之间不能形成连续的支承水膜，水润滑橡胶轴承处于混合润滑状态，导致水润滑轴承界面接触润滑性态复杂多变，黏滑摩擦和刚度阻尼动力系数联合激励诱导轴承产生摩擦振动噪声甚至异常尖锐的鸣音，严重影响潜艇装备的声隐身性能。传统轴承摩擦振动研究中考虑摩擦激励主要简化为静态摩擦模型，并且忽略了系统内部刚度阻尼动力系数的参数激励，难以全面地掌握轴承黏滑振动异常噪声的产生原因，无法准确描述其发展过程，导致现有的减振降噪措施难以达到预期效果，严重制约了潜艇声隐身性能的提升。

技术实现思路

1、本发明为了解决以上问题，提出了一种水润滑轴承界面摩擦振动噪声分析方法。

2、本发明的技术方案是：一种水润滑轴承界面摩擦振动噪声分析方法包括以下步骤：

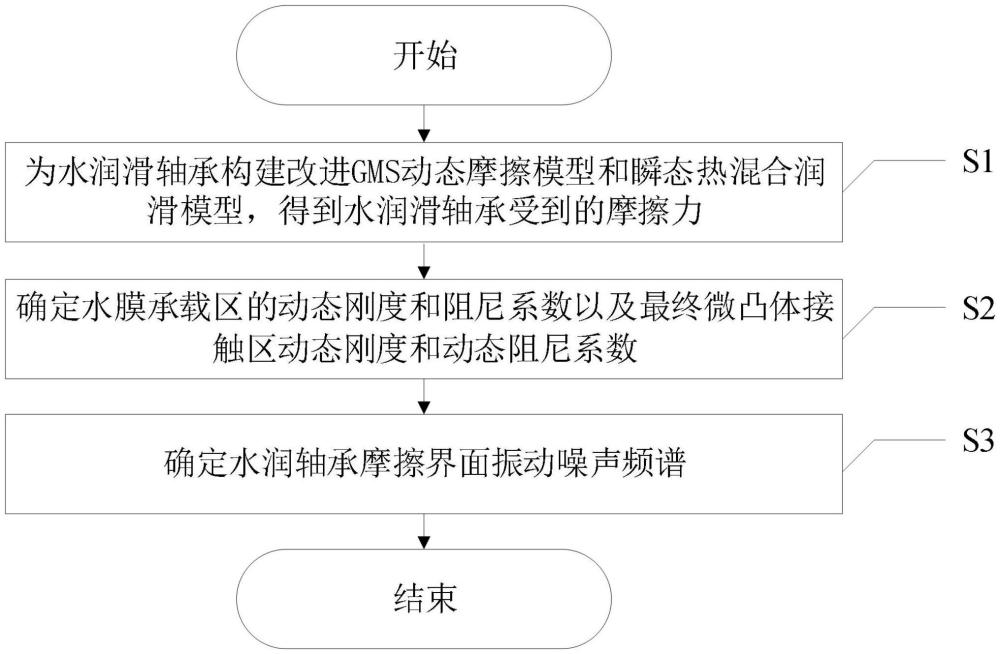
3、s1、为水润滑轴承构建改进gms动态摩擦模型和瞬态热混合润滑模型，并通过改进gms动态摩擦模型，得到水润滑轴承受到的摩擦力；

4、s2、基于瞬态热混合润滑模型，确定水膜承载区的动态刚度和阻尼系数以及最终微凸体接触区动态刚度和动态阻尼系数；

5、s3、根据水润滑轴承受到的摩擦力、水膜承载区的动态刚度和阻尼系数以及最终微凸体接触区动态刚度和动态阻尼系数，确定水润轴承摩擦界面振动噪声频谱。

6、进一步地，s1中，水润滑轴承受到的摩擦力ff(t)的表达式为：

7、

8、式中，n为改进gms动态摩擦模型中的滑块数量，fi(t)为第i个滑块受到的摩擦力，σ(p)为粘性摩擦系数，p为载荷，v(t)为改进gms动态摩擦模型的输入速度；

9、s1中，瞬态热混合润滑模型包括基于瞬态平均雷诺方程、微凸体粗糙接触方程、膜厚方程、弹性变形方程和能量方程；

10、瞬态平均雷诺方程的表达式为：

11、

12、式中，φθ表示第一流量因子，φz表示第二流量因子，φs表示第三流量因子，φc表示接触因子，η表示粘度，ph表示水膜压力，ω表示转速，σ表示轴承摩擦副界面复合粗糙度参数，t表示轴承运转时间，rb表示轴承内径，θ表示轴承圆周方向坐标，z表示轴向方向，h表示水膜厚度；

13、微凸体粗糙接触方程的表达式为：

14、

15、式中，pc表示接触压力，βc表示表面粗糙度参数，k表示硬度系数，表示塑性变形开始时的临界干涉，表示被积函数，h*表示接触面间基于粗糙度的高度；

16、其中，被积函数的一般形式为：

17、

18、式中，z*表示某一粗糙峰基于接触面粗糙峰平均高度的高度，φ*(·)表示z*分布函数，α表示可变常数；

19、膜厚方程h0(θ,z,t)的表达式为：

20、h(θ,z,t)＝c+ecos(θ-ψ)+δδe(θ,z,t)+δδt(θ,z,t)+δhg(θ,z,t)；

21、式中，z表示轴向方向，c表示半径间隙，e表示偏心距，ψ表示偏位角，δδe(·)表示弹性变形方程，δδt(·)表示热变形量，δhg(·)表示沟槽深度；

22、弹性变形方程δδe(θ,z,t)的表达式为：

23、

24、式中，hp表示水膜压力，hc表示接触压力，hp表示轴瓦厚度，v0表示与轴瓦材料泊松比和实际工况相关的常数，v1表示轴瓦泊松比，v2表示主轴泊松比，e1表示轴瓦弹性模量，e2表示主轴弹性模量；

25、能量方程的表达式为：

26、

27、式中，t表示温度，ρ表示密度，cp表示比热容，vr表示径向速度，vθ表示周向速度，vz表示轴向速度，kr表示第一热传导系数，kθ表示第二热传导系数，kz表示第三热传导系数，φ表示热源。

28、进一步地，s2包括以下子步骤：

29、s21、基于瞬态热混合润滑模型，确定水膜承载区的动态刚度和水膜承载区的阻尼系数；

30、s22、确定第一微凸体接触区法向动态阻尼系数、第二微凸体接触区法向动态阻尼系数、第三微凸体接触区法向动态阻尼系数和第四微凸体接触区法向动态阻尼系数；

31、s23、根据第一微凸体接触区法向动态阻尼系数、第二微凸体接触区法向动态阻尼系数、第三微凸体接触区法向动态阻尼系数和第四微凸体接触区法向动态阻尼系数，分别确定第一微凸体接触区动态刚度、第二微凸体接触区动态刚度、第三微凸体接触区动态刚度和第四微凸体接触区动态刚度；

32、s24、根据第一微凸体接触区动态刚度、第二微凸体接触区动态刚度、第三微凸体接触区动态刚度和第四微凸体接触区动态刚度，确定最终微凸体接触区动态刚度；根据第一微凸体接触区法向动态阻尼系数、第二微凸体接触区法向动态阻尼系数、第三微凸体接触区法向动态阻尼系数和第四微凸体接触区法向动态阻尼系数，确定最终微凸体接触区动态阻尼系数。

33、进一步地，s21中，水膜承载区的动态刚度k1(t)的计算公式为：

34、

35、式中，kxx表示力变化方向的刚度系数，kxy表示力变化方向与位移变化方向之间的刚度系数，kyx表示位移变化方向与力变化方向与之间的刚度系数，kyy表示位移变化方向的刚度系数；

36、s21中，水膜承载区的阻尼系数d1(t)的计算公式为：

37、

38、式中，dxx表示力变化方向的阻尼系数，dxy表示力变化方向与位移变化方向之间的阻尼系数，dyx表示位移变化方向与力变化方向与之间的阻尼系数，dyy表示位移变化方向的阻尼系数。

39、进一步地，s22中，第一微凸体接触区法向动态阻尼系数dnn的计算公式为：

40、

41、式中，en为微凸体接触区法向总能量损耗，ω为简谐激振力角频率，xnm为第一法向位移幅值；

42、s22中，第二微凸体接触区法向动态阻尼系数dnτ的计算公式为：

43、

44、式中，ynm为第一切向位移幅值；

45、s22中，第三微凸体接触区法向动态阻尼系数dτn的计算公式为：

46、

47、式中，eτ为微凸体接触区切向总能量损耗，xτm为第二法向位移幅值；

48、s22中，第四微凸体接触区法向动态阻尼系数dττ的计算公式为：

49、

50、式中，yτm为第二切向位移幅值。

51、进一步地，s23中，第一微凸体接触区动态刚度knn的计算公式为：

52、

53、式中，dnn表示第一微凸体接触区法向动态阻尼系数，ω为简谐激振力角频率，tanβn为动态阻尼系数；

54、所述s23中，第二微凸体接触区动态刚度knτ的计算公式为：

55、

56、式中，dnτ表示第二微凸体接触区法向动态阻尼系数，tanγn为动态阻尼系数；

57、所述s23中，第三微凸体接触区动态刚度kτn的计算公式为：

58、

59、式中，dτn表示第三微凸体接触区法向动态阻尼系数，tanβτ为切向损耗系数；

60、所述s23中，第四微凸体接触区动态刚度kττ的计算公式为：

61、

62、式中，dττ表示第四微凸体接触区法向动态阻尼系数，tanγτ为切向损耗系数。

63、进一步地，s24中，最终微凸体接触区动态刚度k2(t)的计算公式为：

64、

65、式中，knn表示第一微凸体接触区动态刚度，knτ表示第二微凸体接触区动态刚度，kτn表示第三微凸体接触区动态刚度，kττ表示第四微凸体接触区动态刚度；

66、s24中，最终微凸体接触区动态阻尼系数d2(t)的计算公式为：

67、

68、式中，dnn表示第一微凸体接触区法向动态阻尼系数，dnτ表示第二微凸体接触区法向动态阻尼系数，dτn表示第三微凸体接触区法向动态阻尼系数，dττ表示第四微凸体接触区法向动态阻尼系数。

69、进一步地，s3包括以下子步骤：

70、s31、根据水润滑轴承受到的摩擦力，得到x方向上的黏滑摩擦力和y方向上的黏滑摩擦力；

71、s32、根据水膜承载区的动态刚度、x方向上的黏滑摩擦力和y方向上的黏滑摩擦力，得到x方向上的动压载荷、y方向上的动压载荷、x方向上的接触载荷和y方向上的接触载荷；

72、s33、根据x方向上的动压载荷、y方向上的动压载荷、x方向上的接触载荷和y方向上的接触载荷，确定水润轴承摩擦界面非线性动力学方程；

73、s34、采用runge-kutta法对水润轴承摩擦界面非线性动力学方程进行数值求解，得到水润轴承摩擦界面的振动响应和结构噪声；

74、s35、根据水润轴承摩擦界面的振动响应和结构噪声，确定水润轴承摩擦界面振动噪声频谱。

75、进一步地，s31中，x方向上的黏滑摩擦力ffx(t)的计算公式为：

76、ffx(t)＝ff(t)cosθ；

77、式中，ff(t)为水润滑轴承受到的摩擦力，θ为圆周方向坐标；

78、s31中，y方向上的黏滑摩擦力ffy(t)的计算公式为：

79、ffy(t)＝ff(t)sinθ；

80、s32中，x方向上的动压载荷fhx(t)、y方向上的动压载荷fhy(t)、x方向上的接触载荷fcx(t)和y方向上的接触载荷fcy(t)的计算公式为：

81、

82、式中，fhx0(t)为平衡位置(x0，y0)处的第一动压载荷，fhv0(t)为平衡位置(x0，y0)处的第二动压载荷，fcx0(t)为平衡位置(x0，y0)处的第一接触载荷，fcv0(t)为平衡位置(x0，y0)处的第二接触载荷，fhx1(t)为因扰动产生的第一动压载荷，fhy1(t)为因扰动产生的第二动压载荷，fcx1(t)为因扰动产生的第一接触载荷，fcy1(t)为因扰动产生的第二接触载荷，fhx2(t)为因扰动产生的第三动压载荷，fhy2(t)为因扰动产生的第四动压载荷，fcx2(t)为因扰动产生的第三接触载荷，fcy2(t)为因扰动产生的第四接触载荷。

83、进一步地，s33中，水润轴承摩擦界面非线性动力学方程的表达式为：

84、

85、式中，mb为水润滑轴承的质量，cb为水润滑轴承基座的支撑阻尼，kb为水润滑轴承基座的支撑刚度，mj为转子的质量，cj为转子基座的支撑阻尼，kj为转子基座的支撑刚度，fhx(t)为x方向上的动压载荷，fcx(t)为x方向上的接触载荷，ffsx(t)为x方向上的混合润滑摩擦力，ffx(t)为x方向上的黏滑摩擦力，fhy(t)为y方向上的动压载荷，fcy(t)为y方向上的接触载荷，ffsy(t)为y方向上的混合润滑摩擦力，ffy(t)为y方向上的黏滑摩擦力，e为偏心位移，f0为静态外载荷，ffκ(t)为κ方向上的接触载荷，ffζ(t)为ζ方向上的接触载荷，x为水平方向的扰动位移，为水平方向的扰动速度，为水平方向的扰动加速度，y为水平方向的扰动位移，为水平方向的扰动速度，为水平方向的扰动加速度，为相对转子在水平方向的扰动加速度，为相对转子在竖直方向的扰动加速度，ω为工作转速。

86、本发明的有益效果是：针对传统水润滑轴承摩擦振动研究中考虑摩擦激励主要简化为静态摩擦模型，并且忽略了系统内部刚度阻尼动力系数的参数激励，难以全面地掌握轴承黏滑振动异常噪声的产生原因的不足，本发明通过改进gms动态摩擦模型和瞬态热混合润滑模型获取时变的黏滑摩擦激励和刚度阻尼动力系数参数激励，并引入轴承摩擦界面非线性动力学分析模型，从而提供一种水润滑轴承界面摩擦振动噪声分析方法。