纤维增强复合材料管道计算优化最大载荷预测方法与流程

本发明涉及复合材料管道力学分析，特别是一种基于三维弹性理论和强度准则的复合材料管道最大轴向弯曲载荷预测方法。

背景技术：

1、纤维增强复合材料管道由于其高比强度、高比模量、耐腐蚀等优异性能，在石油天然气输送、海洋工程、航空航天等领域得到广泛应用。在实际工程中，纤维增强复合材料管道通常承受内压、外压、弯曲、扭转等复杂载荷。尤其是在深海立管、海底管线铺设过程中，纤维增强复合材料管道需要承受较大的弯曲变形。因此，准确预测纤维增强复合材料管道在弯曲载荷下的极限承载能力对于管道的安全高效设计至关重要。

2、尽管现有研究在纤维增强复合材料管道力学行为分析方面取得了重要进展，但仍然存在以下不足：第一、大多数研究仅针对特定铺层角度下复合材料管道的力学性能分析，缺乏对不同铺层角度组合进行系统分析和优选的方法；第二、现有模型大多基于经典层合板理论，忽略了面内剪切应力，计算精度有待提高；第三、鲜有研究能够直观、系统地展示复合材料管道抗弯性能与铺层角度之间的内在关联，不利于工程设计人员快速寻优。

3、综上所述，考虑到工程实际需求，亟需建立一种能够全面考虑铺层角度、堆叠顺序影响，精确预测极限弯曲载荷，并能直观展示抗弯性能的复合材料管道最大载荷预测方法。

技术实现思路

1、针对现有技术的不足，本发明的目的是提供复合材料管道最大轴向弯曲载荷预测方法，通过绘制最大载荷图，直观展示不同铺层角度组合下复合材料管道的抗弯承载能力，为工程设计提供参考依据。

2、为了实现上述目的，本发明采用的技术方案如下：

3、纤维增强复合材料管道计算优化和最大载荷预测方法，包括以下步骤：

4、s100、基于三维弹性理论，建立考虑扩展剪切耦合效应的复合材料管道力学计算模型，得到所述复合材料管道在轴向弯曲载荷下的三维应力分布解析解；

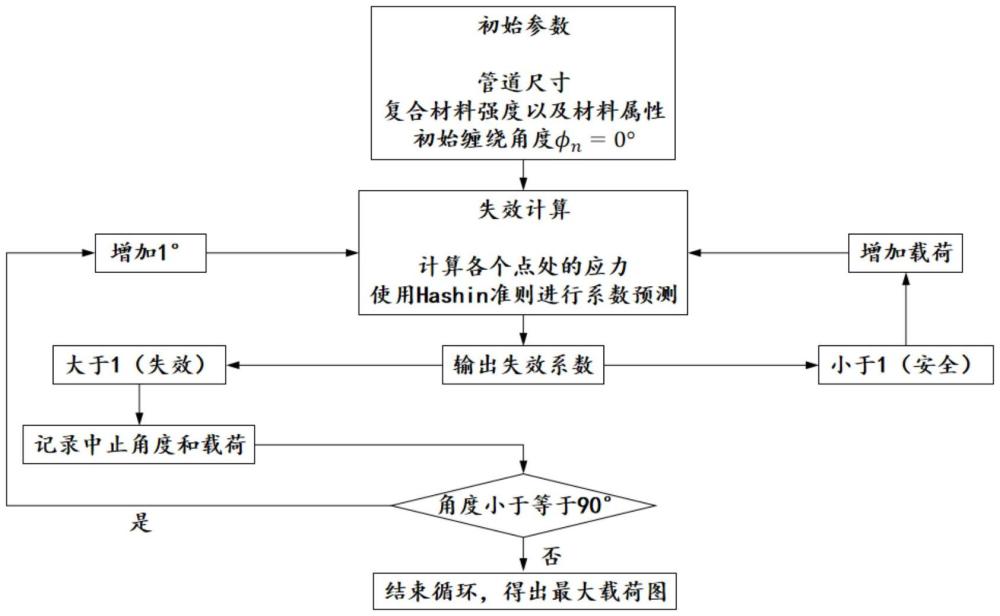
5、s200、将解析解中的应力分量代入hashin强度准则，计算所述复合材料管道的破坏系数，当破坏系数小于1时，将轴向弯曲载荷增加1个增量，直至破坏系数大于1，记录此时的载荷为所述复合材料管道的极限弯曲载荷；

6、s300、改变所述复合材料管道的铺层角度组合，重复步骤s100—s200，直至遍历所有角度组合，得到铺层角度与极限弯曲载荷的对应关系；

7、s400、以不同铺层角度组合为横纵坐标，对应的极限弯曲载荷为纵坐标，绘制所述复合材料管道的最大载荷图。

8、进一步地，所述s100建立考虑扩展剪切耦合效应的所述复合材料管道力学计算模型，包括以下步骤：

9、s101、引入lekhnitskii应力函数，结合广义hooke定律，建立柱坐标系下的本构方程；

10、s102、利用应变协调方程，对lekhnitskii应力函数进一步求解，得到柱坐标系下的应力分量表达式；

11、s103、建立轴向弯曲载荷下的平衡方程、边界条件方程；

12、s104、联立本构方程、应力分量表达式、平衡方程、边界条件方程，求解所述复合材料管道在轴向弯曲载荷下的应力分布解析解。

13、进一步地，s101中引入lekhnitskii应力函数，lekhnitskii应力函数的形式为：

14、f＝κf(r)sinθ

15、ψ＝κψ(r)sinθ

16、式中，f和ψ为应力函数，κ为待定常数，f(r)和ψ(r)为关于径向坐标r的未知函数。

17、进一步地，s102中柱坐标系下的应力分量解析表达式为：

18、

19、

20、式中，σr、σθ、σz分别为径向应力、环向应力和轴向应力；τrθ和τrz分别为径向面上的剪切应力，τθz为面内剪切应力，χi为特征值，αi为待定系数，gi和μi为与材料参数相关的常数。

21、进一步地，s102中利用应变协调方程，对lekhnitskii应力函数进一步求解；

22、柱坐标系中的应变分量包括：径向应变εrr、环向应变εθθ、轴向应变εzz，以及剪切应变分量εrθ、εθz、εzr；在柱坐标系下，应变协调方程的形式如下：

23、

24、进一步地，所述s100中将lekhnitskii应力函数代入应变协调方程，可得：

25、

26、其中，为材料柔度矩阵系数，βij为缩减柔度矩阵系数。

27、进一步地，其中与所述复合材料的本构方程相关，在柱坐标体系中的表达式如下：

28、

29、进一步地，s200中计算所述复合材料管道的破坏系数，当破坏系数小于1时，将轴向弯曲载荷增加1个增量，直至破坏系数大于1，记录此时的载荷为所述复合材料管道的极限弯曲载荷；

30、为预测所述复合材料管道的极限弯曲载荷，采用hashin强度准则对所述复合材料管道的破坏状态进行判定，hashin强度准则在主应力空间内表示为：

31、当σ1≥1时：

32、

33、当σ1<1时：

34、

35、当σ2+σ3≥1时：

36、

37、当σ2+σ3<1时：

38、

39、式中，σ1、σ2、σ3、τ12、τ13、τ23分别为纤维方向正应力、横向正应力、面内剪切应力、层间剪切应力、面上剪切应力；xt、yt分别为纤维方向和横向拉伸强度；xc、yc分别为纤维方向和横向压缩强度；s12、s13、s23分别为面内剪切强度、层间剪切强度、面上剪切强度。

40、进一步地，hashin强度准则计算时，需要将柱坐标系下的应力分量转换到纤维主方向坐标系中，转换公式为：

41、

42、式中，φ为纤维缠绕角度；

43、将转换后的应力分量代入hashin强度准则，即可计算所述复合材料管道任一点处的破坏系数；

44、若破坏系数大于1，则认为该点发生破坏，通过迭代计算，逐步增大轴向弯矩载荷，直至计算的破坏系数均大于1，记录此时的弯矩载荷为所述复合材料管道的极限弯曲载荷。

45、与现有技术相比，本发明具有以下有益效果：

46、(1)基于三维弹性理论建立计算模型，较层合板理论更全面地考虑了扩展剪切耦合效应，计算结果更精确；

47、(2)结合hashin强度准则，可准确预测复合材料管道的极限弯曲载荷；

48、(3)通过绘制最大载荷图，直观展现了铺层角度对复合材料管道抗弯性能的影响规律，可为工程设计提供参考；

49、(4)通过优化铺层角度组合，可最大限度地发挥复合材料的力学性能，显著提高所述复合材料管道的抗弯承载能力。

50、(5)计算效率高，一次计算可得到全部铺层角度工况下的极限弯曲载荷，避免了重复建模和计算。

51、本发明可广泛应用于石油天然气输送、海洋工程、化工管道等领域，对于提高复合材料管道的安全性、可靠性和经济性具有重要意义。