一种考虑空载情况下的基于变密度法的电机拓扑优化方法

本发明隶属于电机拓扑优化设计领域，具体涉及一种考虑空载情况下的基于变密度法的电机拓扑优化方法。

背景技术：

1、拓扑优化作为最高层次的优化方法，突破了传统参数优化的设计理念，通过对有限设计域内有限材料的充分利用及合理布局，对电机结构进行创新构型设计，在保障结构实现高效率、高性能等要求的同时满足结构轻量化的要求。针对电机优化设计领域存在的复杂工况、多约束、高维度的问题，电机拓扑优化方法主要包括离散方法、变密度方法(simp)、水平集方法等。因变密度方法可有效地解决超高维度设计变量的数学规划问题被广泛的应用，该方法的核心思想是将离散设计变量松弛为[0,1]区间的连续设计变量，通过构建虚拟材料密度的非线性插值模型来描述材料属性，使得其转化为连续性优化问题。

2、在多物理场的复杂工况条件下，电机优化设计的轻量化、高性能、高效率等方面的性能指标对基于simp的电机拓扑优化提出了更高的要求。正因电机结构的多种高性能指标，基于simp的电机拓扑优化通常是一个多目标问题，需要对优化目标与约束条件进行有效处理与组合。一般地，基于simp的电机拓扑优化主要是计算电机带载性能，但因输入的正弦电流将会增加其复杂性，导致收敛速度缓慢。并且，优化后的电机拓扑构型具有锯齿状边缘，导致实际制造难度剧增。

技术实现思路

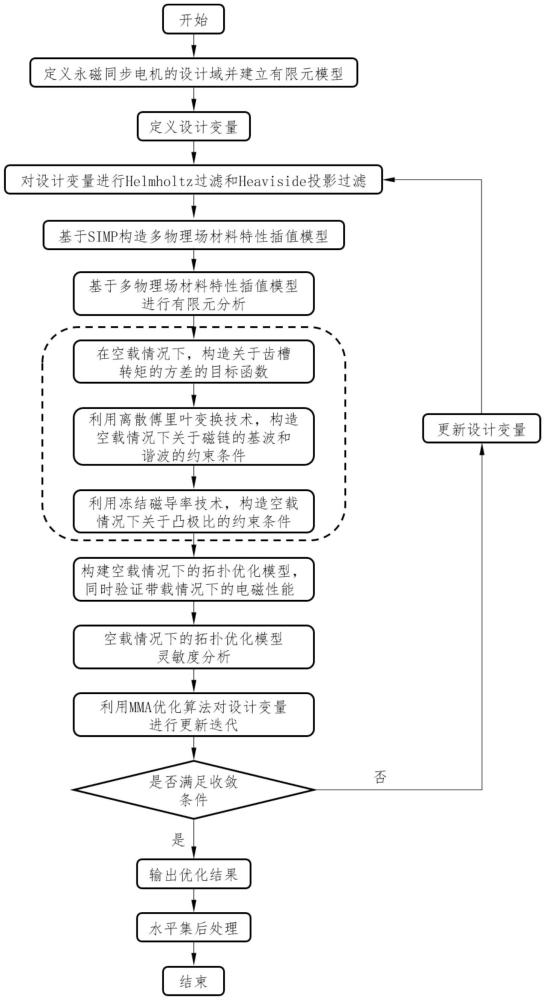
1、为解决综合考虑带载及空载条件下永磁电机拓扑优化的有限元效率问题，本发明提供一种考虑空载情况下的基于变密度法的电机拓扑优化方法。首先，确定转子结构设计域和有限元模型，定义设计变量并进行三场过滤，并基于变密度法构造多物理场材料特性插值模型；然后，构建空载情况下的齿槽转矩方差为目标，磁链基波、磁链总谐波失真率、凸极比、转子柔度及刚度的拓扑优化模型，并通过求解非线性电磁有限元和线性静力学有限元，计算结构性能响应；最后，进行灵敏度分析并采用移动渐近线法(mma)进行优化求解。

2、本发明提供了一种考虑空载情况下的基于变密度法的电机拓扑优化方法，本发明包括如下步骤：

3、步骤1、构建ipmsm几何模型，以1/8的ipmsm转子作为设计域，并利用有限元进行网格剖分；

4、步骤2、定义单元密度ρi为设计变量，即对于各向同性材料，引入单元密度作为设计变量，其变化区间为(0,1]；

5、步骤3、对单元密度ρi进行helmholtz过滤和heaviside投影过滤后得到单元物理密度。helmholtz过滤方程可表示为：

6、

7、其中，为中间密度，ni,j为单元i在过滤半径内的单元集合，ρj为前述集合中的第j个单元的密度，wi,j为权函数可表示为：

8、wi,j＝max(0,r-ri,j)q (2)

9、其中，r为过滤半径，ri,j为单元i质心到单元j质心的距离，q为过滤指数。经过helmholtz过滤后，对中间密度进行heaviside投影过滤后得到单元物理密度，heaviside投影过滤方程可表示为：

10、

11、其中，为单元物理密度，β为投影参数，η为过滤密度的阈值；

12、步骤4、基于simp密度插值模型，构造电磁与力学耦合的材料特性插值模型，其中电磁特性包括磁导率，力学特性包括杨氏模量和物理质量。材料密度与磁导率的插值关系可表示为：

13、

14、其中，ν为磁导率，νfe和νair分别为铁磁材料和空气的磁导率，p为惩罚因子。材料密度与杨氏模量和物理质量的插值关系可表示为：

15、

16、其中，e为杨氏模量，efe为铁磁材料的杨氏模量，m为物理质量，mfe为铁磁材料物理质量向量，⊙为哈达玛积；

17、步骤5、基于电磁与力学耦合的材料特性插值模型，进行有限元分析。电磁场的非线性有限元分析可表示为：

18、sa＝q (7)

19、其中，s为非线性材料的刚度矩阵，a为未知节点矢量磁位，q为激励源向量。静力学场的有限元分析可表示为：

20、ku＝f (8)

21、其中，k为静力学刚度矩阵，u为未知位移向量，f为载荷向量；

22、步骤6、考虑空载情况下，构造关于齿槽转矩的方差为目标函数。利用麦克斯韦张量法计算齿槽转矩，计算公式可表示为：

23、

24、其中，ti为第i个转子位置的齿槽转矩，θelec,i为第i个位置的转子电气角位移，r为气隙圆周半径，l为电机轴向长度，μ0为真空磁导率，br和bt分别为径向和切向磁密，sag为气隙弧度。

25、以齿槽转矩的方差的目标函数可表示为：

26、

27、其中，tvr为齿槽转矩方差，n为转子旋转位置的数量，tav为平均转矩；

28、步骤7、利用离散傅里叶变换技术，构造空载情况下关于磁链的基波和谐波的约束条件。基于有限元分析的结果，每一项绕组磁链的计算公式可表示为：

29、

30、其中，ψk为第k项绕组磁链，θelec为任意一个转子电气角位移，nz为线圈边数，ns为第s个线圈边的导体数，azs为第s个线圈边所在区域的矢量磁位，ds为±1，表示第s个线圈边电流的方向。通过离散傅里叶变换技术，将第k项绕组磁链用不同频次h的磁链谐波之和来表示，转换公式可表示为：

31、

32、其中，h为磁链谐波频次，表示为h＝(0,1,...,m-1)。如果转子旋转位置的数量n为偶数或n＝2m，磁链谐波振幅和可表示为：

33、

34、磁链谐波的幅值可表示为：

35、

36、经过离散傅里叶变换技术后，根据谐波的基础定义，即频次h＝1的波形则为磁链基波，频次h≥2的波形则为高次磁链谐波，构造以磁链基波幅值和总谐波失真率的约束条件，可分别表示为：

37、

38、步骤8、利用冻结磁导率技术，构造空载情况下关于凸极比的约束条件。通过冻结磁导率技术获得电机dq轴电感表征电机凸极比，计算公式可表示为：

39、s＝lq/ld (19)

40、其中，s为凸极比，lq为q轴电感，ld为d轴电感；

41、步骤9、结合以上构造的目标函数和约束条件，构建空载情况下的拓扑优化模型。以齿槽转矩方差为目标函数，应力、质量、柔度、磁链基波幅值、总谐波失真率和凸极比为约束函数的一般拓扑优化模型可表示为：

42、

43、其中，ne为设计域内单元数量，应力、质量、柔度、磁链基波幅值、总谐波失真率和凸极比的约束函数可表示为：

44、

45、其中，为第j个单元的冯·米塞斯应力，σlim为材料的许用应力，i为单位向量，ar为质量百分比，c为转子结构柔度，c0为柔度参考值，ψf0为磁链基波幅值参考值，thd0为总谐波失真率参考值，s0为凸极比参考值。

46、基于一般拓扑优化模型，利用归一化拉格朗日方法构建增广拉格朗日优化框架，可表示为：

47、

48、其中，n＝ne+5为约束函数的数量，p为惩罚项可表示为：

49、

50、其中，μ为二次惩罚因子，为拉格朗日乘子向量。二次惩罚因子和拉格朗日乘子的更新方程可表示为：

51、μ(k+1)＝min[αμ(k),μmax] (25)

52、

53、其中，k为迭代步数，α＞1为更新参数，μmax为防止数值不稳定的上限；

54、步骤10、利用伴随变量法，进行空载情况下的拓扑优化模型的灵敏度分析。由链式法则推导出增广拉格朗日方程对设计变量的灵敏度，可表示为：

55、

56、根据增广拉格朗日方程的组成部分，将增广拉格朗日方程与设计变量的灵敏度可改写为：

57、

58、忽略电磁场和力学场的耦合效应，可将式(28)可简化为：

59、

60、根据式(29)，将增广拉格朗日方程与设计变量的灵敏度拆分为材料属性对设计变量的灵敏度、目标函数和惩罚项分别对材料属性的灵敏度三部分。

61、利用链式法则，以磁导率对设计变量的灵敏度为示例，可表示为：

62、

63、目标函数对单元磁导率的灵敏度可表示为：

64、

65、惩罚项对单元磁导率、单元杨氏模量和单元质量的灵敏度可分别表示为：

66、

67、采用伴随变量法，式(32)、式(33)、式(34)可修改为：

68、

69、

70、式中，为伴随变量，可表示为：

71、

72、步骤11、基于灵敏度信息，采用mma算法对设计变量进行更新迭代；

73、步骤12、判断收敛性。若满足收敛条件，则输出优化结果；若不满足收敛，则返回步骤3，直至满足收敛条件；

74、步骤13、根据simp优化结果进行水平集后处理，得到最终优化结果。

75、进一步地，步骤5中的电磁场的非线性有限元方程sa＝q，采用牛顿拉夫森迭代法求解；静力学场的有限元方程ku＝f中的单元载荷的求解方程表示为：

76、

77、其中，fe为第e个单元的向心力，me为第e个单元的质量，re为设计域内第e个单元的质心距离轴心的距离，ωe为转子角速度。

78、进一步地，步骤6中的平均转矩tav的求解方程可表示为：

79、

80、其中，n为转子旋转位置的数量，ti为第i个转子位置的齿槽转矩。

81、进一步地，步骤8中的凸极比的求解过程中运用了基于电磁关系的绕组磁链求解模型和冻结磁导率技术求解dq轴电感，具体步骤包括：

82、(1)基于基本电磁关系，在三相静止坐标系中的三相定子绕组的全磁链可表示为：

83、

84、其中，θ为转子位置电气角度，ik(k＝1,2,3)为三相定子绕组电流，为永磁体磁场交链三相定子绕组的永磁磁链；lj,k(θ)(j＝1,2,3；k＝1,2,3)为三相定子绕组的自互电感可表示为：

85、

86、采用坐标变化将三相静止坐标系转换为dq转子坐标系中，式(43)可简化为：

87、

88、其中，和ld(θ)和lq(θ)、id和iq、和分别为d轴和q轴的定子绕组全磁链、绕组自互电感、绕组电流、永磁磁链，可分别表示为：

89、

90、(2)因ipmsm拓扑优化模型是在空载ik(k＝1,2,3)＝0的情况下进行的，仅仅考虑了永磁体磁场产生的永磁磁链。所以，为了考虑到ipmsm在带载情况下的电机性能，根据式(45)计算模型，需采用冻结磁导率技术得到dq轴绕组磁链，进而得到dq轴电感。冻结磁导率技术的具体步骤包括：

91、首先，根据式(7)得到的非线性有限元分析结果，冻结设计域内每个单元的磁导率，将非线性磁导率固定为线性磁导率；基于线性磁导率，去除永磁体的影响重新给定激励源向量。仅考虑d轴绕组磁链时，重新给定激励源可表示为：

92、

93、仅考虑q轴绕组磁链时，重新给定激励源向量可表示为：

94、

95、结合线性磁导率和重新给定的激励源向量和进行式(7)的线性有限元分析，得到d轴和q轴的矢量磁位ad和aq。然后，基于线性有限元分析结果，根据式(11)计算d轴和q轴绕组磁链ψd和ψq。

96、因此，基于有限元分析结果得到的ψd和ψq与基于基本电磁关系得到的定子全磁链理论上是相同的，所以根据式(45)获得d轴和q轴的电感。

97、进一步地，步骤9中的一般优化拓扑优化模型中的单元冯·米塞斯应力和转子结构柔度c的计算公式可表示为：

98、

99、c(ρ)＝utku (54)

100、其中，σ＝[σ11,σ22,σ12]τ为柯西应力向量，系数矩阵v0可表示为：

101、

102、进一步地，步骤10中的灵敏度分析，具体步骤包括：

103、目标函数对单元磁导率的灵敏度如式(31)所示，其中齿槽转矩、平均转矩与单元磁导率的导数需采用伴随变量法求解，具体步骤为：

104、(1)首先，令g＝ti，采用伴随变量法，得到：

105、

106、(2)求g对单元磁导率的导数，可表示为：

107、

108、(3)令则得到伴随变量

109、(4)基于步骤(3)，式(57)简化为：

110、

111、(5)以上步骤是基于第i个转子位置的转矩进行推导，所以可表示为：

112、

113、其中，i＝1,...,n为第i个转子位置；

114、(6)根据式(42)，可表示为：

115、

116、其中，n为转子旋转位置的数量。

117、惩罚项对单元磁导率、单元杨氏模量和单元质量的灵敏度如式(32)、式(33)、式(34)所示，需采用伴随变量法进行求解。以惩罚项对单元杨氏模量的灵敏度为例，具体步骤为：

118、(1)根据式(33)，采用伴随变量法，得到：

119、

120、(2)令则得到伴随变量

121、(3)基于步骤(2)，式(61)简化为式(36)的形式。

122、进一步地，步骤13中的水平集后处理的分割法则，具体步骤包括：

123、(1)将单元设计变量映射为节点水平集值，映射方程可表示为：

124、

125、其中，φk为节点水平集值，ni为共用节点k的单元数量，ρmax和ρmin分别为设计变量的最大值和最小值；

126、(2)基于节点水平集值，利用零水平集面切割转子设计域，分割法则表示为：

127、

128、其中，ω+为铁磁材料域，ω-为空气域，为设计域边界。

129、本发明的有益效果是：

130、1、本发明充分考虑电磁性能和力学性能，基于变密度法构造多物理场材料特性插值模型；

131、2、本发明考虑到电机的带载与空载的综合性能，基于多物理场材料特性插值模型，构建一种考虑空载情况下的多物理场拓扑优化模型；

132、3、本发明考虑到优化后电机拓扑构型会出现不平滑边界的问题，引入水平集后处理技术解决此类问题，从而保证电磁性能计算的准确性。