输电铁塔斜柱基础作用力的转换方法、设备及存储介质与流程

本发明涉及输电线路设计，具体涉及一种输电铁塔斜柱基础作用力的转换方法、设备及存储介质。

背景技术：

1、输电线路基础设计是线路设计非常重要的一环。目前，基础立柱主要直柱和斜柱两种型式[1]，其中直柱型式相对常用，但斜柱受力更合理。斜柱基础将立柱坡度与铁塔主材坡度一致，能明显改善基础受力状态，一般下压力 n或上拔力 t稍有增大，但水平力能明显下降，因此斜柱基础具有良好的力学特性和经济性，其在特高压工程、国外输电线路工程中得到了广泛的应用，取得了良好的效果[2~3]。

2、斜柱基础因立柱坡度与铁塔主材坡度一致，其承受的外荷载如何转换和确定是直接影响其优化设计的关键因素。转换的主要思路是将铁塔内力分析得到的直柱坐标系下的基础作用力 n/t、fx、fy转换为斜柱坐标系下的基础作用力 n’ /t’ 、fx’ 、fy’，由于基础作用力复杂多变，国内外学者已对其进行了一些研究，但方法不尽相同。王登科[4]根据斜柱式基础的受力特点，推导出基础立柱计算时的上拔力、下压力及其相应水平力的计算方法，并与相关行业规定计算的结果进行了分析比较。郭青[5]利用空间力系法推导出斜插式基础设计中的力系转换方法，并用《铁塔内力分析程序》进行了验证。鲁先龙[6]根据空间向量投影理论，推导出了直柱式转化为斜柱主材插入式基础荷载的计算方法。得出斜柱基础可有效地改善基础主柱和底板的受力状况，并可显著减少作用在基础上的水平力，提高基础抗倾覆性能。高彬[7]提出了一种斜柱式基础不同力系下荷载转换方法，给出了基础承载力及斜柱本体强度计算时的转换公式。

3、[1].dl/t 5219-2014. 架空输电线路基础设计技术规程[s]. 北京:中国计划出版社,2014.

4、[2].程勇峰, 邵晓军, 朱全军. 我国输电线路基础工程现状及存在的问题[j].电力建设, 2002, 23(3): 32-34.

5、[3].程勇峰, 李正. 输电线路插入式基础和直柱式基础的性状比较[j]. 电力建设, 2003, 24(7): 25-28.

6、[4].王登科. 关于斜柱式基础外负荷确定方法的探讨[j]. 武汉大学学报(工学版), 2007, 40(sup): 223-227.

7、[5].郭青, 贾建民. 送电线路斜插式基础设计中力系转换方法的探讨[j]. 山西电力技术, 1998, 6(83): 20-25.

8、[6].鲁先龙, 程永锋, 张宇. 输电线路斜柱主材插入式基础荷载转换计算[j].电力建设, 2006, 27(6): 21-22.

9、[7].高彬, 曾二贤, 冯衡. 输电铁塔斜柱式基础设计力系转换方法研究[j]. 电网与清洁能源, 2014,30(3): 36-39.

10、[8].蔡士杰译. 计算机图形学(第四版)[m]. 电子工业出版社出版, 2014年.

11、[9].朱雷鸣, 吴晓平, 李建伟等. 直角坐标系的欧拉旋转变换及动力学方程[j]. 海洋测绘, 2010,30(3): 20-22.

12、[10].朱华统. 常用大地坐标系及其变化[m]. 解放军出版社, 1990年.

技术实现思路

1、本发明提出的一种输电铁塔斜柱基础作用力的转换方法、设备及存储介质，可至少解决背景技术中的技术问题之一。

2、为实现上述目的，本发明采用了以下技术方案：

3、一种输电铁塔斜柱基础作用力的转换方法，包括以下步骤，

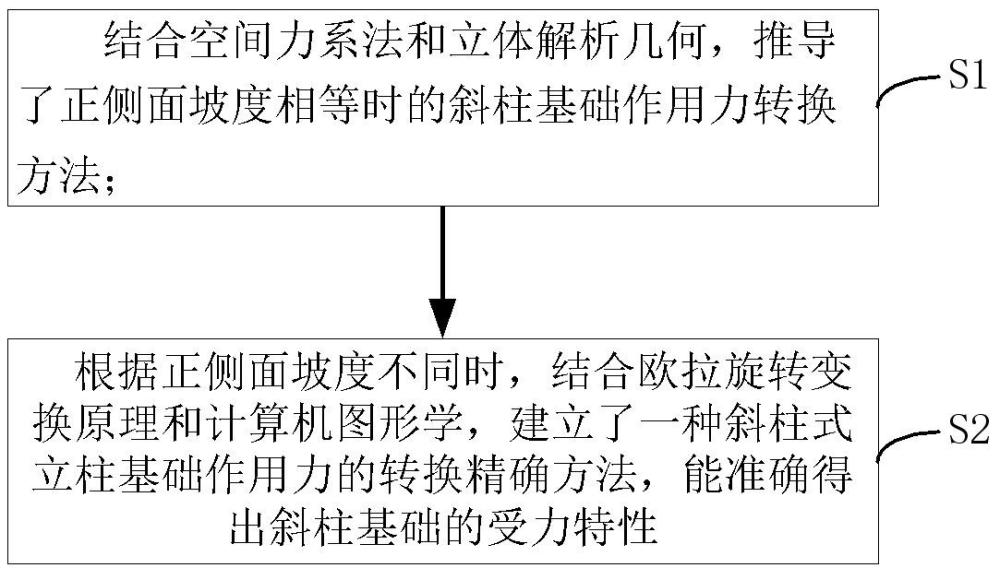
4、s1、结合空间力系法和立体解析几何，推导了正侧面坡度相等时的斜柱基础作用力转换方法；

5、s2、根据正侧面坡度不同时，结合欧拉旋转变换原理和计算机图形学，建立了一种斜柱式立柱基础作用力的转换方法，能准确得出斜柱基础的受力特性。

6、进一步地，步骤s1具体包括：

7、根据计算机图形学三维坐标几何变换，设新坐标系 o’ x’ y’ z’的原点为( x0 ,y0 ,z0)，相对原坐标系的单位坐标矢量表示为：

8、（1）

9、构造坐标旋转矩阵为：

10、（2）

11、构造平移矩阵为：（3）

12、从oxyz到 o’ x’ y’ z’的坐标变换为：（4）

13、若oxyz与 o’ x’ y’ z’坐标系的原点重合，则oxyz到 o’ x’ y’ z’的坐标变换进一步表示为：（5）

14、对于正侧面坡度相等铁塔，三维坐标变换，以主材底部点为原点o，正面oa为x方向，侧面oc为y方向，在主材上选取一点f，画垂直线于e，连接oe和ac交于d点；过a、c点画垂直线交于of线的o’点，连接o’a和o’c；由立体几何原理，of垂直于面o’ac，在ac线上分别确定x’和y’点，使得o’x’⊥o’y’，∠do’x’=∠do’y’=45o，以上就建立了斜柱坐标系 o’ x’ y’ z’，z和 z’方向矢量一致；

15、相应的主材轴线与x、y、z轴的夹角α、β、γ的三角公式为：（7）

16、（8）

17、（9）

18、式中，i为正侧面坡度；

19、由此可得：（10）

20、（11）

21、相应地，o’b的距离可得：

22、；；；（12）

23、根据勾股定理，得到：（13）

24、由等边三角形，可得∣do’∣=∣dx’∣，则可得在oxyz坐标系，x’点和o’的坐标分别为：（14）；（15）；

25、则o’x’的矢量为：（16）

26、相应地，o’x’的模为：（17）

27、则o’x’单位坐标矢量的方向余弦表示为：（18）

28、同理可得在oxyz坐标系，y’点的坐标为：（19）

29、相应地，o’y’的矢量为：（20）

30、则o’y’的单位坐标矢量表示为：（21）

31、而o’z’的矢量为：（22）

32、则o’z’的单位坐标矢量的方向余弦表示为：（23）

33、由此可得，正侧面坡度相等时，作用力的转换公式为：

34、（24）

35、由此根据公式(24)，当铁塔正侧面坡度相等时，就求出相应的斜柱坐标系下的基础作用力。

36、进一步地，步骤s2具体包括，

37、当铁塔正侧面坡度不相等时，引入欧拉旋转变换方法；

38、三维坐标轴沿z方向旋转 θ角度后，由于沿着z轴旋转，新坐标系中z的数值不变，根据欧拉旋转定理，新旧坐标系中数值公式为：（25）

39、式中，xyz为原坐标系； x’ y’ z’为新坐标系； θ为沿z方向旋转角度；

40、写成矩阵表达式为：（26）

41、相应地，旋转矩阵可表示为：（27）

42、同理，沿x、y方向旋转 θ角度后坐标对应关系图，相应的旋转矩阵表示为：（28）

43、若原坐标系沿着x、y、z的顺序进行旋转到新坐标系，则新坐标系下的坐标为：（29）

44、通过相应的旋转，即可求出新坐标系下的坐标数值；假设铁塔正面的坡度为 i1，侧面的坡度为 i2，要将oxyz坐标系旋转至斜柱 o’ x’ y’ z’坐标系，经过以下三步：①先绕z轴逆时针旋转α，形成 o’ x’’’ y’’’ z’’’坐标系；②再先绕y轴顺时针旋转γ，形成 o’ x’’ y’’ z’’坐标系；③最后，再绕z轴顺时针旋转α，形成 o’ x’ y’ z’坐标系；

45、根据以上步骤，按照上述欧拉旋转矩阵原理，则新坐标系下的坐标为：（30）

46、根据三角函数关系，相应的α、γ的三角公式为：（31）（32）

47、将式(31)、(32)代入式(30)中，得铁塔正侧面坡度不相等时，作用力转换旋转矩阵为：（33）

48、由此可得，正侧面坡度不相等时，作用力的转换公式为：（34）

49、当正侧面坡度相等 i1= i2时，可得旋转矩阵[r]的表达式与式(24)是一致的；从式(33)可知，正侧面坡度 i1、 i2是最关键的参数，求出坡度值就转换相应的作用力至斜柱坐标系。

50、又一方面，本发明还公开一种计算机可读存储介质，存储有计算机程序，所述计算机程序被处理器执行时，使得所述处理器执行如上述方法的步骤。

51、再一方面，本发明还公开一种计算机设备，包括存储器和处理器，所述存储器存储有计算机程序，所述计算机程序被所述处理器执行时，使得所述处理器执行如上方法的步骤。

52、由上述技术方案可知，斜柱基础相比直柱基础相比，具有下压力或上拔力增幅不明显、水平力大幅下降的特点，因此在输电线路上得到了广泛的应用，故斜柱基础作用力的正确转换是斜柱基础设计的关键。本发明首先结合空间力系法和立体解析几何，推导了正侧面坡度相等时的斜柱基础作用力转换方法；再次，根据正侧面坡度不同时，结合欧拉旋转变换原理和计算机图形学，建立了一种斜柱式立柱基础作用力的转换精确方法，能准确得出斜柱基础的受力特性；最后，选取110kv~1000kv典型铁塔基础作用力进行对比分析，得出了一些重要结论。本发明提出的斜柱基础作用力的转换精确方法，可作为斜柱斜顶基础（大跨越杆塔基础、深埋基础立柱）的计算、设计的一种有力支撑，在斜柱斜顶基础作用力转换方面有较大的应用前景。