基于多智能体强化学习的异构多机系统动态任务调度方法

本发明涉及多智能体任务调度，特别涉及一种基于多智能体强化学习的异构多机系统动态任务调度方法。

背景技术：

1、近年来，随着机器人技术迅速发展，社会各行业对机器人技术的应用愈发深入，在工业领域中，协作机器人受到广泛关注，重点企业大力推广智能制造模式，以期进一步提高制造业智能化水平和生产效率；服务领域中，由于移动机器人技术和移动互联网、大数据处理等技术进一步融合，移动机器人获得行业龙头关注；特种机器人领域也不断涌现创新应用，如灾后救援，复杂地形探索。但随着机器人应用场景愈发复杂，执行任务的种类和数目也越来越多，早期的单机器人处理方式已经无法满足现阶段的需求，多机器人系统解决方案更具灵活性、可扩展性和突出的协作能力，且大多时候，拥有不同功能，承担不同角色的异构机器人系统更具优势，但随之而来的问题是如何在保证安全性的前提下，更好地协调不同机器人共同完成更复杂的总体任务，因此对异构多机器人系统的合理高效的任务调度至关重要。

2、异构多机器人系统的任务调度问题可以归结为mrta(multi-robot taskallocation)在时间维度扩展的子问题，仍然属于np-hard问题，即该问题在问题规模变大后，合理时间内几乎无法求得精确解。对此，相关研究中比较常见的求解方法有启发式算法，比如根据经验设计启发式规则，依据最早完成时间或最短执行时间等原则来分配任务，该方法对不同规模问题都有一定适应性，但是求解效果欠佳，一般会存在机器人或加工机器出现大量的空闲时间窗口的现象，进而造成整体任务执行的低效；此外还有元启发式算法如遗传算法、粒子群算法、蚁群算法以及各自的变体，这类算法的基本思路都是通过在编码后的候选解空间中以不同范式迭代搜索，最终得出最优或次优解，该类方法在问题规模不大的情况下一般能够得到质量良好的解决方案，但是计算耗时会随着问题规模增长而指数增长，并且对实际场景中存在的动态不确定性不具有鲁棒性。

3、上述研究大部分情况下对实际场景的建模都过于简化，对多机系统大多基于同构的假设，对任务间实际存在的复杂约束探讨的不够深入，并且忽略了实际场景中广泛存在的动态性和不确定性，此外实时性上也很难达到较理想的水平，因此，需要一种能够适应动态环境并能够在合理时间内得出较优解决方案的异构多机器人任务调度方法。

技术实现思路

1、本发明提供了一种基于多智能体强化学习的异构多机系统动态任务调度方法，以解决背景技术所提到的技术问题。

2、为达到上述目的，本发明的技术方案是这样实现的：

3、本发明提供了一种基于多智能体强化学习的异构多机系统动态任务调度方法，具体包括如下步骤：

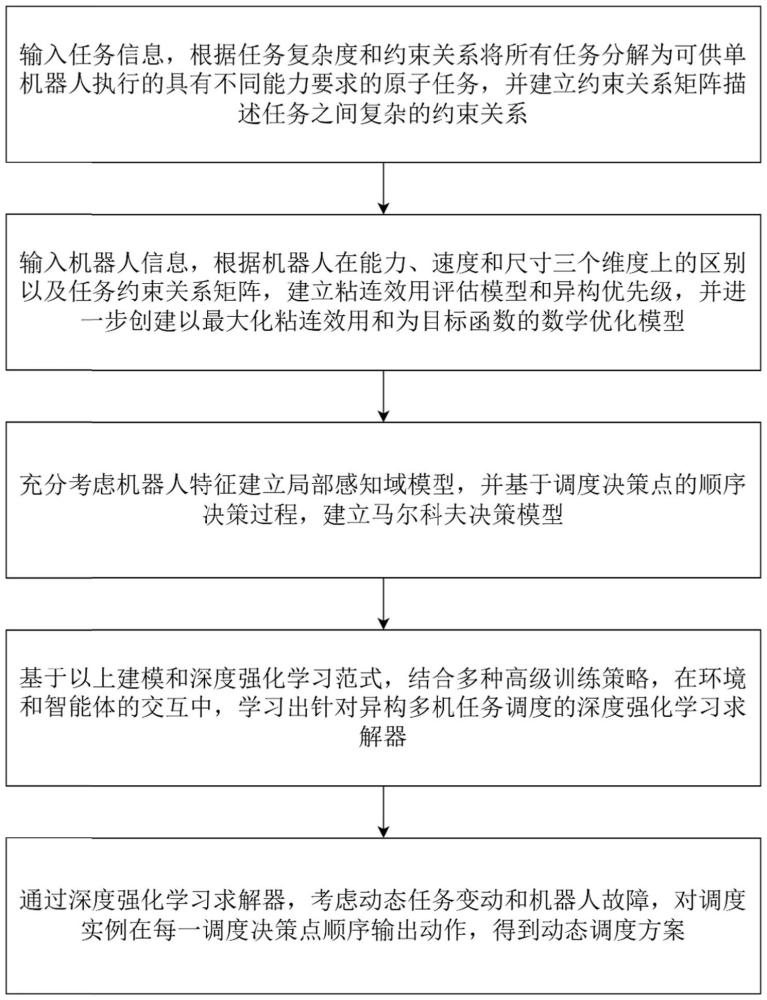
4、s1、输入任务信息，根据任务复杂度和约束关系将所有任务分解为可供单机器人执行的具有不同能力要求的多个原子任务，并建立约束关系矩阵以描述任务之间复杂的约束关系；

5、s2、输入机器人信息，根据机器人在能力、速度和尺寸三个维度上的区别以及约束关系矩阵，建立粘连效用评估模型和异构优先级，并进一步创建以最大化粘连效用和为目标函数的数学优化模型；

6、s3、基于机器人特征建立局部感知域模型，并基于调度决策点的顺序决策过程，建立马尔科夫决策模型；

7、s4、基于以上建模和深度强化学习范式，搭建异构多机系统调度环境，结合多种高级训练策略，在环境和智能体的交互中，学习出针对异构多机任务调度的深度强化学习求解器；

8、s5、通过深度强化学习求解器，考虑动态任务变动和机器人故障，对调度实例在每一调度决策点顺序输出动作，得到动态调度方案。

9、进一步地，所述s1具体包括如下步骤：

10、s11、输入任务信息，并根据任务复杂度和约束关系对输入的任务信息进行任务分类和分解，得到多个原子任务；

11、s12、建立多个原子任务之间的约束关系矩阵，约束关系矩阵包括矩阵元素kj和矩阵元素jk；

12、其中，矩阵元素kj和矩阵元素jk的值均为2，代表原子任务k和原子任务j之间存在关于“原子任务k和原子任务j必须分配给同一机器人”的硬约束，硬约束指的是必须要满足的约束；

13、矩阵元素kj和矩阵元素jk的值均为-2，则代表原子任务k和原子任务j之间存在关于“原子任务k和原子任务j禁止分配给同一机器人”的硬约束；

14、矩阵元素kj为1、矩阵元素jk为-1，则代表原子任务k必须在原子任务j开始之前完成；

15、矩阵元素kj和矩阵元素jk的值为(0,1)或(-1,0)之间的小数，则原子任务k和原子任务j之间存在软约束，即代表原子任务k和原子任务j分配给同一机器人之后，效用会有程度为β的增益或削弱，软约束表示它存在时会对具体原子任务执行产生积极或者消极影响的约束。

16、进一步地，所述s11的实现方式为：

17、对多个独立任务组合而成的复合任务，将其直接拆分为独立的子任务，对于子任务间存在依赖关系的复杂任务，根据依赖不同，分解为不同约束关系的子任务，不论是独立还是存在约束关系的子任务，最终都要分解到单个机器人可以执行并完成的粒度，称之为原子任务；通过任务分类和分解一共得到多个原子任务；

18、每个原子任务的基本信息均由一个五元组表示<pos,utility,exe_time,ability_need,state>，其中pos表示原子任务所在位置，utility表示完成该原子任务的直接效用，exe_time表示机器人完成该原子任务所需执行时间，ability_need表示完成该原子任务所需能力要求，state表示该原子任务是否已被分配以及被分配给哪个机器人。

19、进一步地，所述s2具体包括如下步骤：

20、s21、输入机器人属性，异构系统中机器人的基本信息可由一个五元组表示<cur_pos,left_time,speed,ability,size>，其中cur_pos表示机器人当前位置，left_time表示机器人剩余运行时间，speed表示机器人速度，ability表示机器人完成原子任务的能力等级，size表示机器人的尺寸大小；

21、s22、根据机器人在能力、速度和尺寸三个维度上的区别以及约束关系矩阵，建立粘连效用评估模型；

22、s23、基于能力、速度和尺寸三个异构属性，并根据机器人当前状态构建动态异构优先级列表，从而得到异构优先级；

23、s24、创建以最大化粘连效用和为目标函数的数学优化模型。

24、进一步地，所述s22中的粘连效用评估模型具体如下：

25、

26、式中，uij代表机器人i完成原子任务j的直接效用，代表机器人i完成被分配的所有原子任务后获得的粘连效用；αij代表分配给机器人i的原子任务j的硬约束满足情况；βij代表将原子任务j分配给机器人i时软约束满足情况；ji代表分配给机器人i的所有原子任务的集合。

27、进一步地，所述s24中的数学优化模型具体如下：

28、目标函数：

29、

30、约束条件：

31、(1)单机器人同一时间只能执行一个原子任务；

32、

33、其中，为二进制变量，表示时刻原子任务j是否分配给机器人i，i表示所有机器人的集合；j表示所有原子任务的集合；表示任意；

34、(2)一个原子任务一次只能分配给一个机器人；

35、

36、其中，xij指的是原子任务j的分配情况，若原子任务j分配给了机器人i，则xij等于1，否则为0；

37、(3)机器人完成所有已分配原子任务的时间必须小于tddl；

38、

39、其中，tij表示机器人i执行原子任务j所需执行时间，表示机器人旅行到原子任务j所在位置所需时间，表示机器人在原子任务j处的等待时间，tddl表示原子任务调度的最终时间；

40、(4)机器人的能力和被分配原子任务的能力需求必须相匹配；

41、

42、其中，cij为二进制变量，代表机器人i的能力是否匹配原子任务j的需求；

43、(5)已分配原子任务之间若存在时序约束则需要满足时序约束；

44、

45、其中，δjk为二进制变量，代表原子任务j和原子任务k之间的顺序约束；xnk表示原子任务k是否分配给机器人n；snk代表机器人n开始执行原子任务k的时间点：xmj表示原子任务j是否分配给机器人m；fmj表示机器人m完成原子任务j的时间点；r表示实数集。

46、进一步地，所述s3具体包括如下步骤：

47、s31、通过对机器人速度、能力和所剩资源的综合评估，确定合适大小的局部感知域lpf，局部感知域lpf的半径rlpf计算公式为：

48、rlpf＝ωr×tlim×speed

49、其中，ωr为可调节系数，tlim为机器人可用时间的最大值，speed为机器人速度；

50、然后对局部感知域lpf的半径rlpf内可见原子任务进行效用评估，筛选出可行原子任务，并计算出马尔科夫建模内状态空间中局部状态信息的三个指标，三个指标分别为局部感知域中特殊原子任务对机器人的吸引度att_s、局部感知域中时序原子任务对机器人的吸引度att_t以及局部感知域中距离最近的原子任务对机器人的吸引度att_g；

51、至此，得到局部感知域模型；

52、s32、并基于调度决策点的顺序决策过程，建立马尔科夫决策模型；马尔科夫决策模型包括状态空间、动作空间、奖励函数以及状态转移；

53、其中，状态空间主要包括三个部分，分别是决策机器人个体状态信息、局部状态信息和全局状态信息，决策机器人个体状态信息均来自机器人属性；局部状态信息包括与该机器人最相关的原子任务信息；

54、动作空间包括两类启发式规则，分别是优先规则和探索规则，二者均作用于局部感知域内的可用原子任务，优先规则更加侧重于获取短期效用；探索规则是一个复合动作，更加侧重于获取长远的潜在效用，且不一定会得到与该规则匹配的具体原子任务；优先规则指的是三个优先级动作，具体分别是：1、选择满足能力约束的最近空闲任务；2、选择有特殊能力需求中的最近空闲任务；3、选择满足时序约束中的最高优先级的空闲任务；

55、奖励函数的结构主要有三部分：动作有效的基本奖励、不同动作生效时的额外鼓励以及不同动作失效时的惩罚；

56、状态转移指的是每当时间步到达一个调度决策点时，就会触发状态转移，再次根据当前异构优先级列表，选择下一顺位机器人作为决策机器人，基于该机器人状态和环境的具体状态得到下一状态，以此类推，直到当机器人的剩余时间全部用完时，将会退出优先级列表不再参与顺序决策，而当所有机器人都无足够剩余运行时间时，进入终止状态。

57、进一步地，所述s32中的奖励函数具体如下：

58、

59、其中，r表示奖励函数；u为动作选择的原子任务的效用，tused为完成该原子任务所用的总时间，w1、w2和w3分别代表s32中三个优先级动作生效的布尔值，w代表探索动作是否生效的布尔值。

60、进一步地，所述s4具体包括如下步骤：

61、s41、基于粘连效用评估模型、数学优化模型、局部感知域模型以及马尔科夫决策模型和深度强化学习范式，搭建异构多机系统调度环境；

62、s42、引入行为网络和目标网络，其中行为网络用于选择动作，目标网络用于评估动作的q值，q值为状态-动作价值，表示在某个特定状态下采取某个特定动作的长期累积回报的期望值，而目标值是目标网络对q值的估计值；目标值的计算公式如下：

63、

64、其中，γ为折扣系数，θt是t时间步行为网络的参数，θ-是目标网络的参数；q(.)表示行为网络或目标网络；在目标值的公式中，括号内的q(.)表示行为网络，括号外的q(.)表示目标网络；rt代表第t个时间步环境反馈的奖励值；st+1表示第t+1时间步的状态；at+1表示第t+1时间步的动作；

65、并约定行为网络和目标网络之间的参数关系，计算目标q值的目标网络仅通过上述参数关系跟随行为网络做软更新，参数关系具体为：

66、θ-＝λ·θt+(1-λ)·θ-

67、其中，λ是一个固定数值，且λ＜＜1；

68、s43、利用dueling dqn训练策略，并通过改变行为网络和目标网络的内部架构，将目标网络对q值的直接预测分解为状态价值和相对状态价值的动作优势值，以提高对状态-动作价值评估的准确性，并进一步在异构多机系统调度环境中对行为网络和目标网络进行训练，直至奖励函数的奖励曲线收敛，得到训练后的行为网络和目标网络，并将训练后的行为网络和目标网络作为深度强化学习求解器。

69、进一步地，所述s5具体包括如下步骤：

70、s51、将调度实例初始时刻的状态信息输入深度强化学习求解器，深度强化学习求解器输出动作，根据动作对应的启发式规则确定具体原子任务分配，原子任务和机器人属性发生相应变化，更新状态，重复上述过程得到静态调度方案；

71、s52、根据静态调度方案和当前时刻原子任务执行情况确定不同调度决策点的信息，若发生动态事件，则插入动态调度决策点，根据动态调度决策点的相关信息，并按照异构优先级按顺序输入对应时刻状态，然后调用深度强化学习求解器实时求解，得到若干候选解，选择候选解中最合适的机器人-原子任务分配，更新调度方案，得到动态调度方案。

72、本发明的有益效果：

73、本发明提供了一种基于多智能体强化学习的异构多机系统动态任务调度方法，通过对任务间复杂约束关系建立粘连效用评估模型和基于局部感知域描述马尔科夫决策模型，搭建了异构多机系统调度环境，然后基于强化学习训练范式使用双重对抗q网络(即采用了对抗网络架构的行为网络和目标网络)训练得到深度强化学习求解器，基于深度强化学习求解器的调度流程可以快速对调度问题求出高效的调度方案，并能够对动态事件以插入动态调度决策点的方式处理任务执行过程中的不确定性，实现快速鲁棒的动态任务调度。