一种基于数字孪生的机电作动器状态反演方法与流程

本发明涉及航空机电作动器控制的，特别是一种基于数字孪生的机电作动器状态反演方法。

背景技术：

1、多电/全电飞机(mea/aea)的发展使其得到了越来越多的关注，与此相关的功率电传技术(power-by-wire，pbw)也在航空航天领域中得到了广泛的应用。在这项技术中，功率电传作动器被广泛使用。机电作动器(electromechanical actuator，ema)是一种新型功率电传作动器，相对于传统的液压和电液作动器，其具有很多优点。它不仅能够提供高效的能量转换，还可以减少能源损耗和环境污染，提高系统可靠性和维护性，以及减少重量和占用空间。由于其优越的性能，机电作动器被越来越广泛地应用于多电/全电飞机上。作为一种有潜力的新型机电设备，机电作动器具有广泛的应用前景，为未来的航空航天行业提供更多的机遇和挑战。

2、机电作动(ema)系统的高功率密度设计与封闭的传动结构集成在一起，通常运行于有限的空间和恶劣的环境。由于安装空间有限，ema无法进行完备的传感器配置，而且部分和健康状态相关的状态参数很难通过传感器直接获取也需要借助状态反演、参数辨识技术来获取。因此，状态反演和健康状态评估有着极强的关联性，进而决定其在飞机上能否被广泛应用。

3、数字孪生技术可以辅助机电作动(ema)系统的状态反演。这是基于数字孪生在全生命周期运行和优化的基本要求。数字孪生体是和物理实体相对独立存在于和物理空间有差异的虚拟作用域里并且可以在全周期运行的信息综合体。全生命周期运行可以理解为当存在一个物理实体的状态时，必然有一个数字孪生体与之对应，存在一个虚拟状态与之对应。这种演变有助于在设备运行状态反演、监测与预测维护方面提供有效的助力和抓手。同时，基于数据的注入、集成和融合，dt将实际运行的物理状态信息反演映射到虚拟空间也会对优化决策、监测健康状况以及预测剩余使用寿命(rul)做到视情维修(cbm)等领域即将出现的问题方面有很大帮助。

技术实现思路

1、为了解决上述的技术问题，本发明提出了一种基于数字孪生的机电作动器状态反演方法，通过获取ema多健康工作状态下的多源数据信息，并将所述多源数据信息在时间维度根据健康指标划分为不同的试验数据集；对所述数据集内的多源数据信息进行预处理，归并相似的数据形成验证调整过的多源信息数据集；对所述多源信息数据集内每一种多源数据信息注入到建立的ema数字孪生模型中；采用遗传算法优化数字孪生模型，对实际运行的参数进行识别、估计并反演映射到孪生空间。

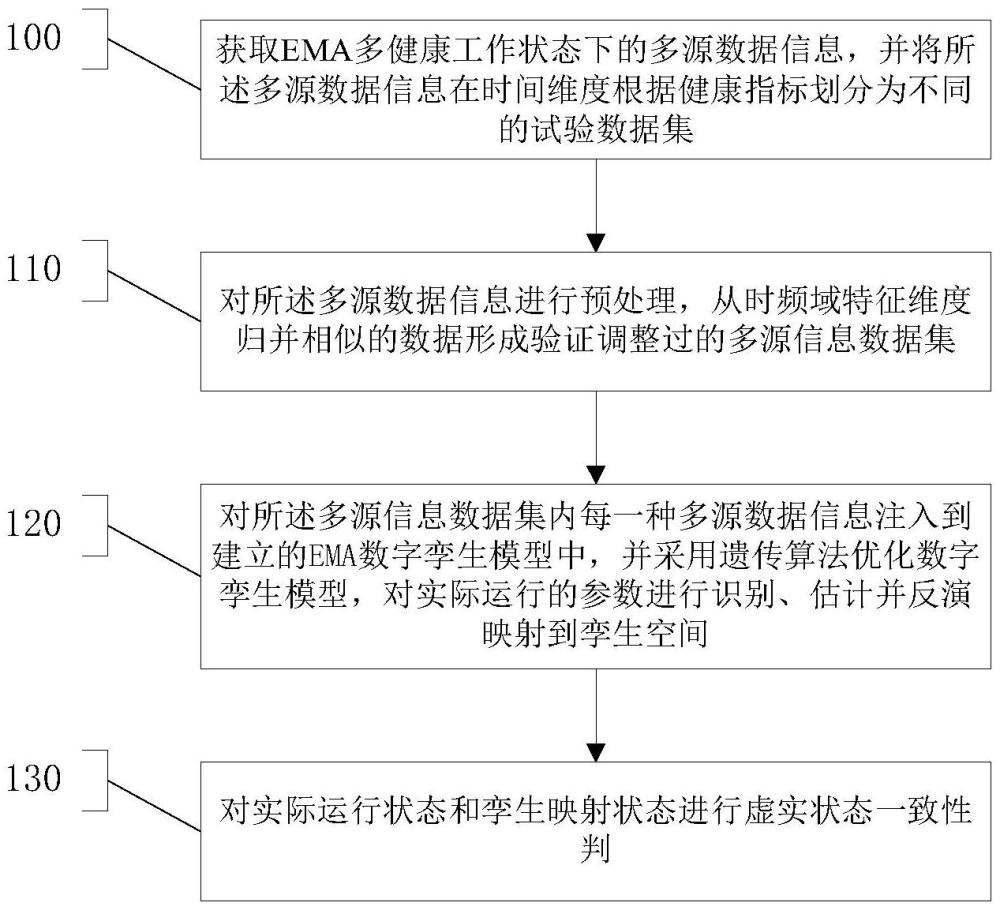
2、本发明的目的是提供一种基于数字孪生的机电作动器状态反演方法，包括获取ema多健康工作状态下的多源数据信息，并将所述多源数据信息在时间维度根据健康指标划分为不同的试验数据集，还包括以下步骤：

3、步骤1：对所述多源数据信息进行预处理，从时频域特征维度归并相似的数据形成验证调整过的多源信息数据集；

4、步骤2：对所述多源信息数据集内每一种多源数据信息注入到建立的ema数字孪生模型中，并采用遗传算法优化数字孪生模型，对实际运行的参数进行识别、估计并反演映射到孪生空间；

5、步骤3：对实际运行状态和孪生映射状态进行虚实状态一致性判别。

6、优选的是，所述多源数据信息包括电机电流信号(i1,i2,i3)、电机电压信号(u1,u2,u3)、转速信号(v)、转矩信号(t)、振动信号(a)和位移传感器信号(x)，共10维原始数据信息。

7、在上述任一方案中优选的是，所述试验数据集包括磨损四状态数据集d1～4，表示为：d1＝{i1 1,i1 2,i1 3,u1 1,u1 2,u1 3,v1,t1,a1,x1}、d2＝{i2 1,i2 2,i2 3,u21,u22,u2 3,v2,t2,a2,x2}、d3＝{i3 1,i3 2,i3 3,u3 1,u3 2,u3 3,v3,t3,a3,x3}以及d4＝{i41,i4 2,i4 3,u4 1,u4 2,u4 3,v4,t4,a4,x4}，其中，d1为系统正常数据集，d2为轻度磨损数据集，d3为中度磨损数据集，d4为重度磨损数据集。

8、在上述任一方案中优选的是，所述磨损四状态包括系统正常、轻度磨损、中度磨损和重度磨损。

9、在上述任一方案中优选的是，所述步骤1包括以下子步骤：

10、步骤11：提取时域特征；

11、步骤12：提取频域特征；

12、步骤13：提取时频域特征；

13、步骤14：计算余弦距离dis(xi,xj)，用于衡量两个向量的差异。

14、在上述任一方案中优选的是，所述时域特征包括波形因子s、波峰因子c、脉冲因子i、峭度因子k和裕度因子l，

15、所述波形因子s的计算公式为

16、

17、所述波峰因子c的计算公式为

18、

19、所述脉冲因子i的计算公式为

20、

21、所述峭度因子k的计算公式为

22、

23、所述裕度因子l的计算公式为

24、

25、其中，x(t)为数据集a1中的检测信号，t为检测信号数，n为采集的信号总数。

26、在上述任一方案中优选的是，所述频域特征包括重心频率fc、均方频率msf和频率方差vf，

27、所述重心频率fc的计算公式为

28、

29、所述均方频率msf的计算公式为

30、

31、所述频率方差vf的计算公式为

32、

33、其中，s(f)为功率谱函数，f为频率，df为频率微分符号。

34、在上述任一方案中优选的是，所述功率谱函数s(f)的计算公式为

35、

36、其中，f[]表示傅里叶变换，m＝1,2,…,n/2。

37、在上述任一方案中优选的是，所述步骤13包括计算j层上第i个节点的能量值e(j,i)，公式为

38、

39、将小波包分解后信号能量谱中各频带的能量百分比特征di作为故障诊断特征值，计算公式为：

40、

41、其中，pv为小波变换系数，为范数的平方，di为将小波包分解后信号能量谱中各频带的能量百分比特征。

42、在上述任一方案中优选的是，所述余弦距离dist(xi,xj)的计算公式为

43、

44、其中，xi为第i个样本的特征向量，xj为第j个样本的特征向量，xik为第i个样本的特征向量的第k维特征值，xjk为第j个样本的特征向量的第k维特征值，k为特征向量维度，θ为特征向量之间的角度，n为特征向量的维度总数。

45、在上述任一方案中优选的是，所述ema数字孪生模型为

46、

47、

48、其中，ua为电机三相电压的a相电压，ub为电机三相电压的b相电压，uc为电机三相电压的c相电压，rs(t)为电机定子绕组阻值，ia为电机三相电流的a相电流，ib为电机三相电流的b相电流，ic为电机三相电流的c相电流，d为电机三相电流的d相电流，dt为时间的微分符号，ψa为电机a相磁链，ψb为电机b相磁链，ψc为电机c相磁链，la为a相绕组自感，lb为b相绕组自感，lc为c相绕组自感，mab为ab相绕组互感，mac为ac相绕组互感，mba为ba相绕组互感，mbc为bc相绕组互感，mca为ca相绕组互感，mcb为cb相绕组互感，ψf为永磁体磁链，θe为电角度。

49、在上述任一方案中优选的是，所述步骤2还包括将park变换应用于三相静止坐标系下的电压方程以及磁链方程中，并考虑到温度对于绕组阻值的影响，得到d-q轴下的两项电压以及磁链，

50、所述电压方程为

51、

52、所述磁链方程为

53、

54、其中，ud为park变换后的d轴电压，uq为park变换后的q轴电压，为定子电阻绕组阻值的修正值，id为d轴电流，iq为q轴电流，ψd为d轴磁链，ψq为q轴磁链，ωm为电机转子的机械角速度，ld为d轴自感，lq为q轴自感，ψf(t)为磁体磁链，为永磁体磁链的修正值，ψf(t)为磁体磁链。

55、在上述任一方案中优选的是，电机的电磁转矩方程为

56、

57、其中，p为电机的极对数。

58、在上述任一方案中优选的是，电机的运动学方程为

59、

60、其中，tl为负载转矩，j为电机负载折算到电机输出轴端的转动惯量，b为电阻的阻尼系数，dω为角速度微分符号，ω为角速度。

61、在上述任一方案中优选的是，ema动力学模型中，滚珠丝杠的输入端力矩方程为

62、

63、丝杠动力学方程为

64、

65、其中，tl2为滚珠丝杠输入力矩，fg为丝杠和螺母之间的轴向力，cbs为滚珠丝杠和螺母之间的轴向等效刚度，tf3为滚珠丝杠和螺母之间的等效摩擦力矩，θn为转动角度，ε2为滚珠丝杠和螺母之间的间隙，xema为丝杠端部位移，dbs为滚珠丝杠和螺母之间的轴向等效粘性摩擦系数，ωn为角速度，vema为丝杠端部移动速度，l为滚珠丝杠导程。

66、在上述任一方案中优选的是，所述步骤2还包括当物理采集数据注入到ema数字孪生后,在虚拟空间生成数据，这些生成的数据用ddt＝{idt 1,idt2,idt 3,udt 1,udt 2,udt3,vdt,tdt,adt,xdt}来表示，

67、其中，idt 1,idt 2,idt 3,udt 1,udt 2,udt 3是作为输入量和物理信息保持一致，vdt,tdt,adt,xdt是待反演量需要通过优化模型来反演并保持和物理空间一致。

68、在上述任一方案中优选的是，所述遗传算法包括以下子步骤：

69、步骤21：将待反演参数进行二进制编码，形成遗传算法中的基因和染色体；

70、步骤22：初始化并选择初始种群进行优化；

71、步骤23：利用交叉、变异算子生成子代种群；

72、步骤24：进行适应性判别，保留优良个体确保好的基因、染色体；

73、步骤25：迭代后，选取最优个体作为当前的最优解；

74、步骤26：参数解码，获取最优的反演参数。

75、在上述任一方案中优选的是，所述一致性判别方法为判定dist(dpt,ddt)<δ是否成立，

76、其中，dpt就是物理采集到的信息d1～4，ddt为数据映射到数字孪生中产生的数据。

77、在上述任一方案中优选的是，所述步骤3还包括采用留一法队反演的精度进行量化，当基于一个n样本集x＝{x(i)|x(i)＝(x(i)1,x(i)2,…,x(i)3),i＝1,2,3,…,n}，反演模型表示为rx(x)，公式为

78、rx(x)＝βtψ(x)

79、其中，βt为反演模型各多项式的权值向量，ψ为反演模型的各个多项式。

80、同时,设置留一样本集拥有n-1个样本表示为x～j＝{x(i)|x(i)＝(x(i)1,x(i)2,…,x(i)3),i＝1,2,3,…,j-1,j+1,…,n}并将定义为基于留一样本集的反演模型，将反演的误差定义为rx(x)和的差值

81、

82、并将对样本集上所有的反演误差累积，定义为留一误差，公式为：

83、

84、反演精度为：

85、

86、其中y＝{y1,y2,…,yn}为反演后的参数，当反演精度高于预设的值时，认为反演的结果具有可信性，和实际运行状态保持一致。

87、本发明提出了一种基于数字孪生的机电作动器状态反演方法，提高复杂机电设备状态反演与实际运行状态的一致性以及参数反演准确率。