碎裂岩体滑坡预应力锚索刚弹性桩位移计算方法

本发明涉及滑坡灾害防治的，尤其涉及一种碎裂岩体滑坡预应力锚索刚弹性桩位移计算方法，特别是指在破碎裂隙发育岩质滑坡下的预应力锚索刚弹性桩设计计算。

背景技术：

1、预应力锚索抗滑桩作为一种有效的滑坡加固措施，因其具有较强的抗滑力、受力合理等特点常用于大型滑坡防治工程中，其桩体的位移是评估其结构稳定性和耐久性的重要指标。而现有的锚索桩计算方法在计算碎裂岩体滑坡存在一定的局限性，主要存在以下问题：1、目前采用预应力锚索刚性桩计算方法时桩身位移过小，采用预应力锚索弹性桩计算方法时桩身位移偏大；2、现有的锚索桩计算方法无法考虑滑面以下地质环境演化影响，尤其是碎裂岩体劣化对桩体内力计算的不利影响；3、锚索实际拉力按经验值取值，取值方法不够明确；4、锚索与桩的荷载分配不明确，锚索荷载分配不够，往往不能发挥结构整体作用，造成极大的浪费。

技术实现思路

1、针对上述背景技术中存在的技术问题，本发明提出一种碎裂岩体滑坡预应力锚索刚弹性桩位移计算方法，计算了在碎裂岩质滑坡作用下，预应力锚索刚弹性桩的桩身位移；预测了预应力锚索刚弹性桩的变形状况；检验了预应力锚索刚弹性桩在滑坡推力作用下是否安全；为预应力锚索刚弹性桩的结构设计提供依据。

2、为了达到上述目的，本发明的技术方案是这样实现的：

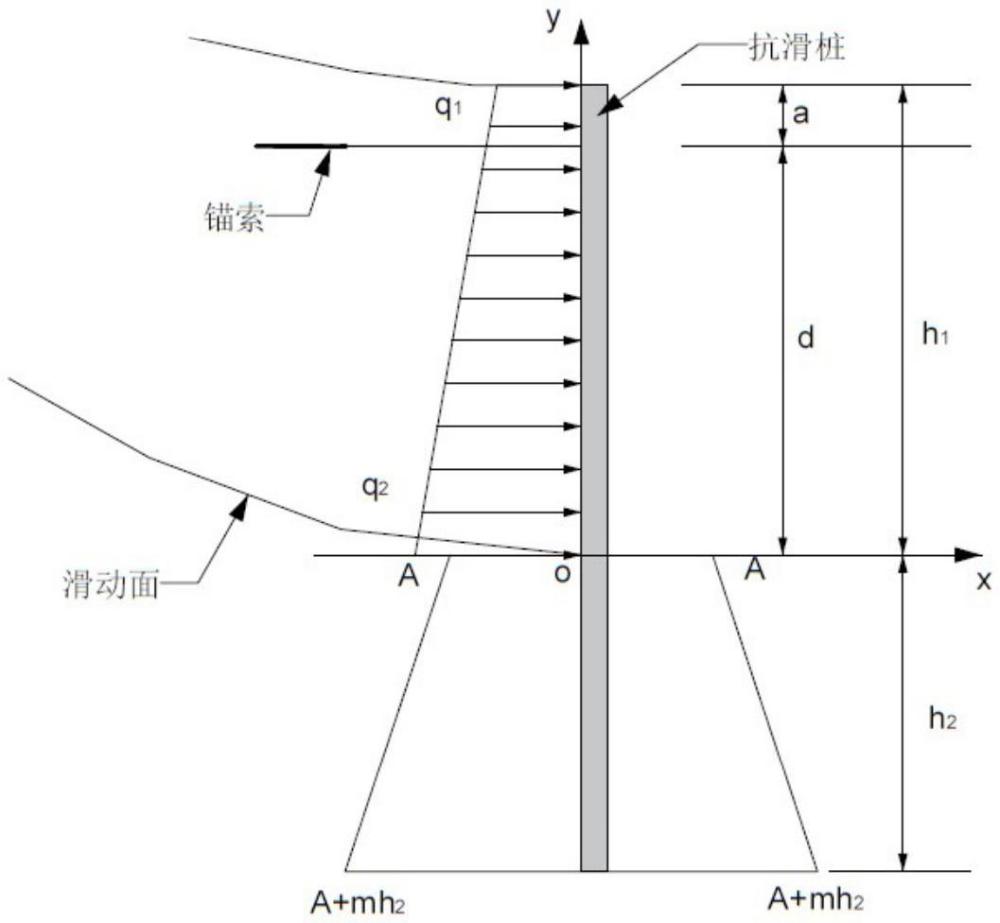
3、一种碎裂岩体滑坡预应力锚索刚弹性桩位移计算方法，碎裂岩质滑坡预应力锚索刚弹性桩包括抗滑桩、锚索和锚礅；抗滑桩的桩顶设有锚索，锚索一端固定在桩顶锚礅上，另一端固定在边坡稳定的岩土体中；

4、所述碎裂岩体滑坡预应力锚索刚弹性桩位移计算方法：

5、步骤一：假定预应力抗滑桩承受滑坡推力、锚索拉力及锚固段桩周土作用力；并设定抗滑桩在滑面以上的桩长为h1、滑面以下的桩长为h2、桩的计算宽度为bp；

6、步骤二：考虑桩身发生初始刚性变形时，通过搭建预应力锚索刚性桩的计算模型，计算得到锚索伸长后的初始拉力；

7、步骤三：当裂隙岩体劣化以后，考虑桩体发生弹性挠曲变形时，通过构建预应力锚索刚弹性桩的计算模型计算得到锚索的最终拉力；

8、步骤四：基于锚索的最终拉力计算预应力锚索刚弹性桩桩身内力及位移。

9、步骤二中，预应力锚索刚弹性桩的计算模型包括：

10、桩在锚点处的水平位移方程为：

11、

12、锚索在桩锚点处的水平伸长量方程为：

13、f1＝δ(p1-p0)；

14、锚点处桩、锚位移变形协调方程为：

15、δ1＝f1；

16、其中，d为锚点距滑动面的距离，δ为锚索的柔度系数，p0为锚索的初始预应力，在此阶段，p1为锚索伸长后的初始拉力，为桩的转动角度，y1为桩的转动点距锚固段顶端的距离；li为锚索自由段长度，as为每束锚索截面积，eg为锚索的弹性模量，n为每孔锚索的束数；δ1为桩在锚点处的水平位移，f1为锚索在锚点处的水平伸长量。

17、所述锚索伸长后的初始拉力p1的计算方法为：

18、滑坡推力作用下，滑面处桩体的剪力q0和弯矩m0分别为：

19、

20、其中，q1为滑坡推力在桩顶的强度分布，q2为滑坡推力在滑面处的强度分布；

21、此阶段，滑坡推力及锚索拉力作用下，根据材料力学、悬臂桩的计算原理，滑面处桩体初始剪力q1和初始弯矩m1分别为：

22、q1＝q0-p1

23、m1＝m0-p1d

24、此阶段，桩底处剪力、弯矩平衡方程为：

25、

26、其中，a为滑动面处的地基系数，m为地基比例系数，y表示计算点距锚固段顶端的距离；q1为作用在桩锚固段顶剪力，m1为作用在桩锚固段顶弯矩；

27、此阶段，根据上述桩底处剪力、弯矩平衡方程得到桩的转动角度

28、

29、此阶段，根据上述桩底处剪力、弯矩平衡方程得到桩的转动点距锚固段顶端的距离y1：

30、

31、此阶段，根据锚点处桩、锚位移变形协调方程δ1＝f1得到锚索伸长后的拉力，表示为：

32、

33、步骤三中，预应力锚索刚弹性桩的计算模型包括：

34、在滑坡推力作用下，锚点处桩身位移为：

35、

36、其中，e为抗滑桩的弹性模量，i为抗滑桩的惯性矩，δiq为滑坡推力作用下锚点处桩身位移；

37、在锚索拉力作用下，锚点处桩身位移为：

38、

39、其中，p2为锚索最终拉力，δip为锚索初始拉力p1作用下锚点处桩身位移；

40、桩在锚点处的水平位移方程为：

41、δ2＝δiq+δip

42、锚索在桩锚点处的水平位移方程为：

43、f2＝δ(p2-p1)

44、锚点处桩、锚位移变形协调方程为：

45、δ2＝f2

46、其中，δ2为滑坡推力及锚索初始拉力作用下锚点处桩身位移，f2为锚索的水平伸长量。

47、所述锚索最终拉力p2的计算方法为：

48、碎桩体发生弹性挠曲变形时，根据材料力学计算原理，滑面处桩体最终剪力q2和弯矩m2为：

49、q2＝q0-p2

50、m2＝m0-p2d

51、当桩体发生转动时，嵌固段桩周土将对桩体产生弹性抗力，滑面处桩受到的剪力、弯矩为q2、m2，将视桩底为自由端，根据桩嵌固段受力，建立平衡方程；因此，桩底处剪力、弯矩平衡方程为：

52、

53、其中，为桩的转动角度；

54、此阶段，根据上述桩底处剪力、弯矩平衡方程求解得出桩的转动角度

55、

56、此阶段，根据上述桩底处剪力、弯矩平衡方程求解得出桩的转动点距锚固段顶端的最终距离y2：

57、

58、根据锚点处桩、锚位移变形协调方程δ2＝f2，得到锚索最终拉力计算公式：

59、

60、在步骤四中，预应力锚索刚弹性桩桩身内力及位移的计算分为三个阶段，分别表示如下：

61、阶段一：0<y≤a，当桩顶至锚点时，预应力锚索刚弹性桩桩身内力及位移的计算方法为：

62、

63、阶段二：a<y≤h1，当锚点至滑面处时，预应力锚索刚弹性桩桩身内力及位移的计算方法为：

64、

65、

66、阶段三：0≤y≤h2，当在滑动面以下时，预应力锚索刚弹性桩桩身内力及位移的计算方法为：

67、

68、其中，y为计算点至滑动面的距离，qi为桩身截面剪力，mi为桩身截面弯矩，xi为桩身位移，σi为锚固段桩侧弹性抗力。

69、本发明的有益效果：1)本发明推导出了碎裂岩质滑坡预应力锚索刚弹性桩位移计算方法，解决了刚性桩位移计算过小，弹性桩位移计算过大情况；

70、2)本发明可以考虑滑面以下岩土劣化对计算的影响，推导了刚弹性桩内力计算公式，解决了刚性桩内力计算偏大的问题，使得内力计算结果更加符合实际，同时也节约工程造价；

71、3)本发明提出了考虑碎裂岩体劣化条件下锚索桩变形协调后，锚索实际拉力计算方法，使得锚索与桩承担滑坡推力分配更明确，而不是采用经验估值；

72、4)本发明给出了不同截面尺寸情况下，矩形截面桩身能够承担的正负最大弯矩比，为锚索根数选择提供上限，同时能够最大限度发挥结构作用，使结构受力更合理，节约了工程造价。