一种翼型绕流仿真算法的制作方法

本发明涉及数值计算和数值模拟，尤其是一种翼型绕流仿真算法。

背景技术：

1、计算机辅助工程分析是现代工业数字化领域的重要组成部分，在飞机、船舶、汽车等行业有着及其广泛与深入的应用，数值仿真是其中非常核心的技术。对于翼型绕流进行数值仿真，能够辅助相关工作人员更高效、更经济地进行飞机翼型的设计和验证。

2、现有技术中大多复杂计算区域下的数值仿真都依赖于贴体网格的生成，这种方法低效，稳定性低，同时难以保证计算质量。

技术实现思路

1、为了克服上述现有技术中的缺陷，本发明提供一种翼型绕流仿真算法，使用符号距离函数表示计算区域，使用inverse lax-wendroff方法处理复杂边界，能够在笛卡尔网格上处理翼型的复杂边界问题，避免了贴体网格的生成，保证了仿真的计算稳定性和效率。

2、为实现上述目的，本发明采用以下技术方案，包括：

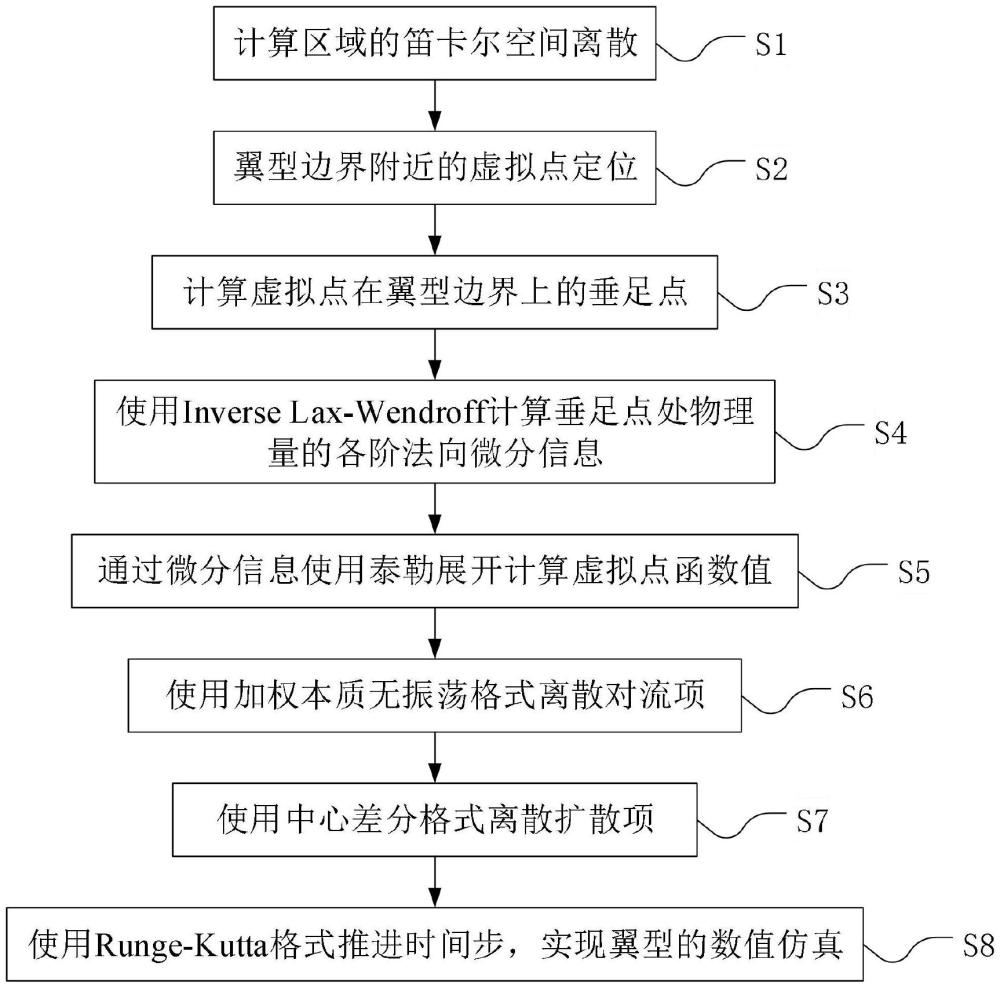
3、一种翼型绕流仿真算法，具体包括以下步骤：

4、s1，对计算区域进行均匀笛卡尔离散；

5、s2，在计算区域边界，即翼型的几何边界附近，定位虚拟点；所述虚拟点为参与计算但是落在计算区域外部的格点；

6、s3，计算虚拟点落在翼型边界上的垂足点；

7、s4，对每个落在翼型边界上的垂足点，计算各个物理量在垂足点的各阶法向微分信息；

8、s5，通过各个物理量在垂足点的各阶法向微分信息以及泰勒展开算法计算虚拟点的格点函数值；

9、s6，使用虚拟点的格点函数值以及内部函数值，通过三阶加权本质无振荡的格式计算离散的对流项；

10、s7，使用虚拟点的格点函数值以及内部函数值，通过四阶中心差分的格式计算离散的扩散项；

11、s8，使用runge-kutta格式向前推进时间步，实现翼型绕流数值仿真模拟。

12、优选的，步骤s1的具体过程如下：

13、对计算区域进行横平竖直的均匀笛卡尔离散，给定计算区域[xl,xr]×[yl,yr]，将空间离散在x轴方向离散为nx份，y方向离散为ny份，空间离散的格点坐标记作xi,j＝(xi,yj)，具体如下：

14、

15、

16、

17、同时对于控制方程：

18、

19、其中u＝(ρ,ρu,ρv,e)t为变量，f(u)＝(ρu,ρu2+p,ρuv,u(e+p))t和g(u)＝(ρv,ρuv,ρv2+p,v(e+p))t，和为对流项，和为扩散项；

20、应力张量满足：

21、

22、其中，ρ为密度；u＝(u,v)为速度，u为x方向的速度，v为y方向的速度；e为能量；p为压强；re为雷诺数；γ＝1.4是比热容比；pr是普朗特数；为声速；cx和cy是声速c在x和y方向的分量，为温度；

23、压强满足状态方程：||·||为向量模长的计算符号。

24、优选的，步骤s2中，给定翼型的符号距离函数表示φ(x)，虚拟点定位算法为：{xi,j|-2h≤φ(xi,j)≤0}，h＝max(hx,hy)；记虚拟点集合为g，其中，符号距离函数φ(x)满足，对于给定的翼型ω，翼型边界为对于空间中任何一个点x，有：

25、

26、其中，ωc为ω的补集。

27、优选的，步骤s3中，通过垂足计算算法，计算虚拟点落在翼型边界上的垂足点，具体计算方法为：对于任何一个虚拟点xg∈g，其在翼型边界上的垂足点为x*，其中，为梯度算子。

28、优选的，步骤s4中，对每个落在翼型边界上的垂足点，计算u,v,ρ,t在该点的0，1，2阶法向微分信息，记为f，其中，f为对应的物理量，f∈u,v,ρ,t；n为垂足点处的外法向方向。

29、优选的，步骤s4中，计算垂足点处物理量的各阶微分信息，具体计算方法如下：

30、s41，在垂足点x*进行局部坐标旋转，使得新的坐标系的x轴和垂足点的法向方向相同，同时将速度场也进行旋转；

31、s42，根据翼型边界条件，固壁恒温边界条件转化方程，此时边界条件为u＝ub,v＝vb,t＝tb，将方程转化为变量为u＝(ρ,u,v,t)t的方程，转化后的方程的形式为：ut+aux＝buxx+rhs；其中，矩阵a和b为：

32、

33、

34、rhs为右端项，由原始方程计算得到；

35、s43，最小二乘外推，通过垂足点附近的内部格点函数值构造最小二乘系统，估计垂足点处原始变量u＝(ρ,u,v,t)t的0，1，2阶微分信息，记作

36、s44，特征分解，利用fext计算将矩阵a在垂足点的值为aext，并将其相似对角化，可以得到特征值系统rext,λext,lext，满足aext＝rextλextlext，λext＝diag{ub-c,ub,ub,ub+c}，而后得到特征变量v＝lextu

37、其中，

38、v＝(v1,v2,v3,v4)

39、

40、s45，零阶ilw微分信息的计算，求解如下方程组，变量为uilw,vilw,tilw,ρilw：

41、

42、s46，一阶ilw微分信息的计算，求解如下方程组，变量为

43、其中，为随体导数，满足

44、s47，二阶ilw微分信息的计算，求解如下方程组，变量为

45、其中，

46、

47、s48，凸组合，计算最终的0，1，2阶法向微分信息为：

48、

49、其中，

50、

51、s49，重新旋转，在垂足点x*旋转，旋转到原来的坐标系。

52、优选的，步骤s5中，通过各个物理量在垂足点的各阶法向微分信息以及泰勒展开算法计算虚拟点的格点函数值，具体计算方法为：

53、

54、其中，s＝||xg-x*||。

55、优选的，步骤s8中，使用runge-kutta格式向前推进时间步，实现翼型绕流数值仿真模拟，具体如下所示：

56、对于控制方程，空间离散之后可以写成时间步长通过cfl条件计算为δt，记当前时间步为n，当前时间为t＝tn，则下一步时间为tn+1＝tn+δt，有：

57、

58、其中，中出现的对流项以及扩散项通过s6和s7计算得到；为中间变量。

59、优选的，步骤s7中，使用虚拟点的格点函数值以及内部函数值，通过四阶中心差分的格式计算离散的扩散项，对于物理量f，扩散项中出现的导数计算公式如下：

60、

61、

62、

63、

64、

65、其中，(fxx)i,j为的离散逼近，(fyy)i,j为的离散逼近，(fxy)i,j为的离散逼近，(fx)i,j为的离散逼近，(fy)i,j为的离散逼近。

66、优选的，步骤s6中，针对对流项f(u)x的离散算法，对于格点(xi,yj)，以及ui,j＝u(xi,yj,t)，由于具体计算流程中j的值不影响计算算法，因此在算法描述时忽视下标j，具体流程如下：

67、s61，计算

68、s62，特征分解，计算的导数矩阵并进行相似对角化，可以得到特征值系统满足其中都是4×4大小的矩阵，且为对角矩阵，满足将得到的矩阵忽视下标，记作

69、s63，特征分解，投影到局部特征空间，对于原始变量ui，得到特征变量vi＝lui以及流通量fi在特征空间的投影其中，

70、

71、s64，lax-friedrichs流分裂技术，对v和的每个分量，计算得到：

72、

73、其中，下标k＝1,2,3,4；

74、后续计算忽视下标k，对所有的k，操作均相同；

75、s65，计算

76、而后计算光滑因子

77、计算非线性权重

78、其中

79、计算

80、s66，计算

81、计算

82、s67，计算

83、s68，计算对流项的离散

84、本发明的优点在于：

85、(1)本发明使用inverse lax-wendroff方法实现在笛卡尔网格上的高精度边界处理，从而实现整个仿真算法的高精度化，能够在笛卡尔网格下处理复杂边界问题。

86、(2)本发明的计算格式和边界处理都有理论三阶精度，其中时间格式采用的是三阶tvd runge-kutta格式，扩散项的离散采用的是四阶中心差分格式，对流项离散采用的是三阶weno格式，边界处理使用了二次多项式插值，保证了三阶精度，能够保证最后仿真的精度。

87、(3)本发明的内部计算算法采用的是weno格式，这个格式能够分辨间断，从而能够捕捉到间断，因此在高速情形下也能适用。

88、(4)本发明使用符号距离函数表示计算区域，使用inverse lax-wendroff方法处理复杂边界，能够在笛卡尔网格上处理翼型的复杂边界问题，避免了贴体网格的生成，保证了仿真的计算稳定性和效率。

89、(5)本发明通过符号距离函数表示翼型的几何，保证可以快速定位虚拟点和快速计算虚拟点的垂足，从而提高了计算效率。

90、(6)本发明使用inverse lax-wendroff方法计算垂足点处物理量的各阶微分信息，inverse lax-wendroff算法会利用到方程和时间的微分信息以及边界条件，从而保证垂足点微分信息和内部计算区域以及控制方程的物理一致性，从而保证了计算的稳定性。同时，这个方法在笛卡尔网格上实行，从而可以实现在翼型仿真过程中的复杂边界处理。

91、(7)本发明使用格点函数值以及内部函数值，通过三阶加权本质无振荡的格式计算离散的对流项，加权本质无振荡的格式是一种能够捕捉激波的格式，这种格式将一阶格式用非线性权重进行凸组合，能够在光滑的计算区域保证三阶精度，在不光滑的计算区域保证计算的稳定性。