一种有向无环图结构的学习方法及系统

本技术涉及有向无环图，尤其是涉及一种有向无环图结构的学习方法及系统。

背景技术：

1、由于真实世界中普遍存在的不确定性，推理系统需要考虑到不同事件发生的可能性。概率图模型（probability graph model, pgm）为研究人员从这些静态数据集中挖掘出变量之间的关联信息，解释数据中隐藏的含义并实现高效的概率推理提供了可行的形式框架。它通过概率论运算为每一种可能发生的事件赋予一个概率使研究人员能够考虑到一些不太可能但又不是完全不可能的选项，从而获得一种更符合现实情况的推理模型，并通过图模型紧凑的表示复杂分布中的结构，使得推理模型被有效的表达和利用。近年来，概率图模型已成为人工智能和机器学习的热门研究领域，在计算机视觉、语音识别和风险评估等多个领域成功应用。在利用概率图模型进行不确定推理之前，需要先根据领域知识构造出概率图模型。过去，概率图模型的构造通常由领域专家利用专业知识进行人工构造，但是该过程耗时长而且实现过程复杂。在当今的信息时代，从样本数据中学习概率图模型已成为主要的构造手段。

2、常用的概率图模型主要是有向无环图（directed acyclic graph, dag）和无向图模型（undirected graph）。有向无环图是一种图形工具，它提供了一种直观地表示和更好地理解因果关系、混淆和偏差等关键概念的方法。有向无环图学习需要从样本数据中找到与数据匹配度最好的网络结构，因此，如何从海量的样本数据中学习出与数据匹配度最好、精度最高的有向无环图成为了亟待解决的技术问题。

技术实现思路

1、为了从海量的样本数据中学习出与数据匹配度最好、精度最高的有向无环图，本技术提供一种有向无环图结构的学习方法、系统、设备及存储介质。

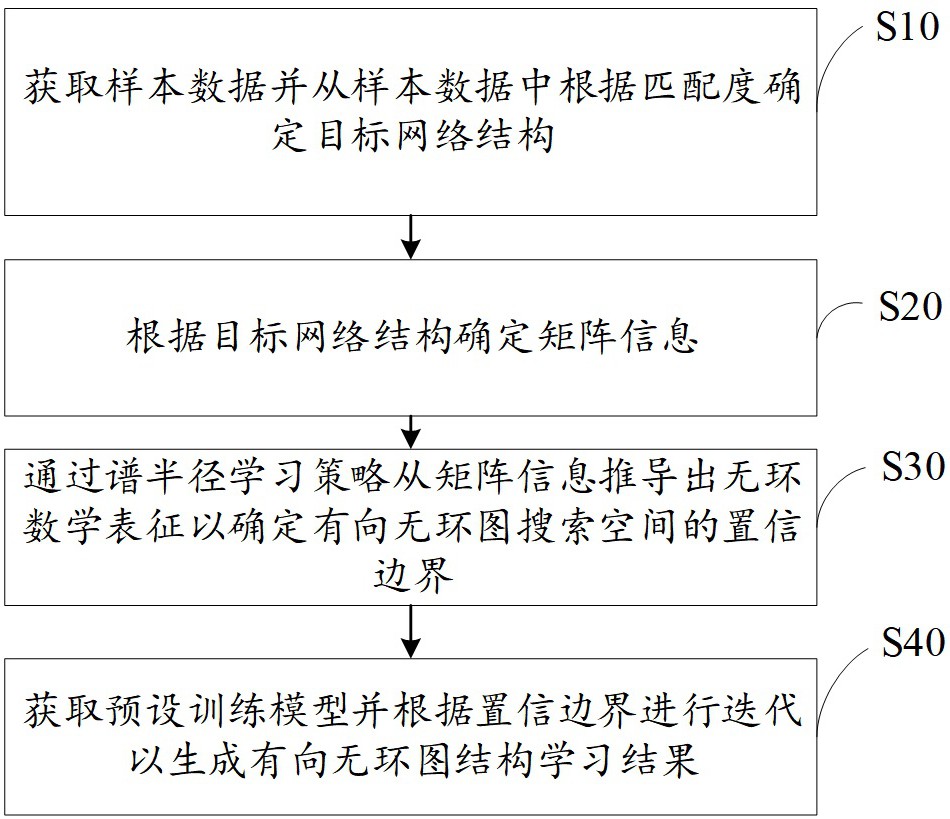
2、第一方面，本技术提供的一种有向无环图结构的学习方法采用如下的技术方案：

3、一种有向无环图结构的学习方法，包括：

4、获取样本数据并从所述样本数据中根据匹配度确定目标网络结构；

5、根据所述目标网络结构确定矩阵信息；

6、通过谱半径学习策略从所述矩阵信息推导出无环数学表征以确定有向无环图搜索空间的置信边界；

7、获取预设训练模型并根据所述置信边界进行迭代以生成有向无环图结构学习结果；

8、其中，所述根据所述目标网络结构确定矩阵信息的步骤，包括：

9、根据所述目标网络结构确定基于分数的结构学习表示以确定矩阵信息

10、

11、其中，是一个评分函数，是由加权邻接矩阵导出的个节点的图，当且仅当是有向边；

12、其中，所述根据所述目标网络结构确定基于分数的结构学习表示以确定矩阵信息的步骤之后，还包括：

13、通过将所述结构学习表示中的作为幂零矩阵，将所述结构学习表示转化为连续优化问题

14、

15、其中，所述幂零矩阵的特征值均为0；

16、在所述连续优化问题中，定义实矩阵，是所述实矩阵的所有特征值；

17、确定迹，行列式；

18、根据所述迹和所述行列式确定矩阵信息；

19、其中，所述通过谱半径学习策略从所述矩阵信息推导出无环数学表征以确定有向无环图搜索空间的置信边界的步骤，包括：

20、根据所述矩阵信息中的迹进行推导以生成第一推导结果；

21、根据所述矩阵信息中的行列式进行推导以生成第二推导结果；

22、根据所述第一推导结果和所述第二推导结果确定最终推导目标；

23、根据谱半径学习策略结合所述最终推导目标在所述矩阵信息中推导出无环数学表征以确定有向无环图搜索空间的置信边界；

24、其中，所述根据谱半径学习策略结合所述最终推导目标在所述矩阵信息中推导出无环数学表征以确定所述有向无环图搜索空间的置信边界的步骤，包括：

25、根据所述矩阵信息确定目标连续优化问题

26、

27、其中，是单位矩阵，是矩阵的行列数，表示所述矩阵信息中对应的hadamard积的特征值，是的hadamard积的谱半径；

28、设是连通图，在范围内，分析谱半径的精确范围，以确定所述有向无环图搜索空间的置信边界

29、

30、其中，代表所述有向无环图的平均度，代表所述有向无环图最大度。

31、可选的，所述根据所述第一推导结果和所述第二推导结果确定最终推导目标的步骤，包括：

32、根据所述第一推导结果确定所述矩阵信息中的迹对应的第一计算复杂度信息；

33、根据所述第二推导结果确定所述矩阵信息中的行列式对应的第二计算复杂度信息；

34、对所述第一计算复杂度信息和所述第二计算复杂度信息进行比较以确定最终推导目标。

35、可选的，所述获取预设训练模型并根据所述置信边界进行迭代以生成有向无环图结构学习结果的步骤，包括：

36、获取预设训练模型，所述预设训练模型采用基于图自编码器的深度生成模型dag-gnn作为生成模型框架；

37、在所述预设训练模型中确定

38、

39、其中，为输入样本数据，为输出生成数据，是特征变量，是单位矩阵，为训练邻接矩阵，为的转置矩阵，是多层感知机的神经网络，将定义为，将标识映射定义为，设为，为所述预设训练模型的恒等式映射以更新所述预设训练模型；

40、获取当前预设训练模型

41、

42、其中，是对应的神经网络的参数，是对应的神经网络的参数；

43、通过最大化证据下限策略对所述预设训练模型进行迭代以生成有向无环图结构学习结果。

44、第二方面，本技术提供一种有向无环图结构的学习系统，包括：

45、结构确定模块，用于获取样本数据并从所述样本数据中根据匹配度确定目标网络结构；

46、矩阵信息确定模块，用于根据所述目标网络结构确定矩阵信息；

47、置信边界模块，用于通过谱半径学习策略从所述矩阵信息推导出无环数学表征以确定有向无环图搜索空间的置信边界；

48、预设训练模型模块，用于获取预设训练模型并根据所述置信边界进行迭代以生成有向无环图结构学习结果；

49、其中，所述矩阵信息确定模块，用于根据所述目标网络结构确定基于分数的结构学习表示以确定矩阵信息

50、

51、其中，是一个评分函数，是由加权邻接矩阵导出的个节点的图，当且仅当是有向边；

52、其中，所述矩阵信息确定模块，用于通过将所述结构学习表示中的作为幂零矩阵，将所述结构学习表示转化为连续优化问题

53、

54、其中，所述幂零矩阵的特征值均为0；

55、在所述连续优化问题中，定义实矩阵，是所述实矩阵的所有特征值；

56、确定迹，行列式；

57、根据所述迹和所述行列式确定矩阵信息；

58、其中，所述置信边界模块，用于根据所述矩阵信息中的迹进行推导以生成第一推导结果；

59、根据所述矩阵信息中的行列式进行推导以生成第二推导结果；

60、根据所述第一推导结果和所述第二推导结果确定最终推导目标；

61、根据谱半径学习策略结合所述最终推导目标在所述矩阵信息中推导出无环数学表征以确定有向无环图搜索空间的置信边界；

62、其中，所述置信边界模块，用于根据所述矩阵信息确定目标连续优化问题

63、

64、其中，是单位矩阵，是矩阵的行列数，表示所述矩阵信息中对应的hadamard积的特征值，是的hadamard积的谱半径；

65、设是连通图，在范围内，分析谱半径的精确范围，以确定所述有向无环图搜索空间的置信边界

66、

67、其中，代表所述有向无环图的平均度，代表所述有向无环图最大度。

68、第三方面，本技术提供一种计算机设备，所述设备包括：存储器、处理器，所述处理器在运行所述存储器存储的计算机指令时，执行如上文所述的方法。

69、第四方面，本技术提供一种计算机可读存储介质，存储有指令，当所述指令在计算机上运行时，使得计算机执行如上文所述的方法。

70、综上描述，本技术包括以下有益技术效果：

71、本技术通过获取样本数据并根据匹配度确定目标网络结构；根据目标网络结构确定矩阵信息；通过谱半径学习策略从矩阵信息推导出无环数学表征以确定置信边界；获取预设训练模型并根据置信边界进行迭代以生成有向无环图结构学习结果；利用有向图的谱半径构建新的无环性数学表征，研究连续优化的有向无环图结构学习方法。为连续优化的有向无环图学习提供新的学习框架。