三维重建方法、装置、设备、存储介质及产品与流程

本公开涉及三维重建，尤其涉及一种三维重建方法、装置、设备、存储介质及产品。

背景技术：

1、艺术家们利用先进的二维平面设计软件创造了大量精美的二维平面设计，从简约的图形设计到复杂的卡通形象的设计，无一不彰显着艺术家的独特视角与精湛技艺。

2、然而，随着数字技术的飞速发展，观众对于视觉体验要求的日益提升，三维模型能够赋予作品更加立体、生动的视觉效果，使观众能够更直观地感受到设计背后的空间感与深度，从而增强作品的感染力和沉浸感。因此，将二维图形转成它所表达的三维模型的需求就自然产生了。

技术实现思路

1、本发明提供一种三维重建方法、装置、设备、存储介质及产品，实现自动将二维图形转成它所表达的三维模型。

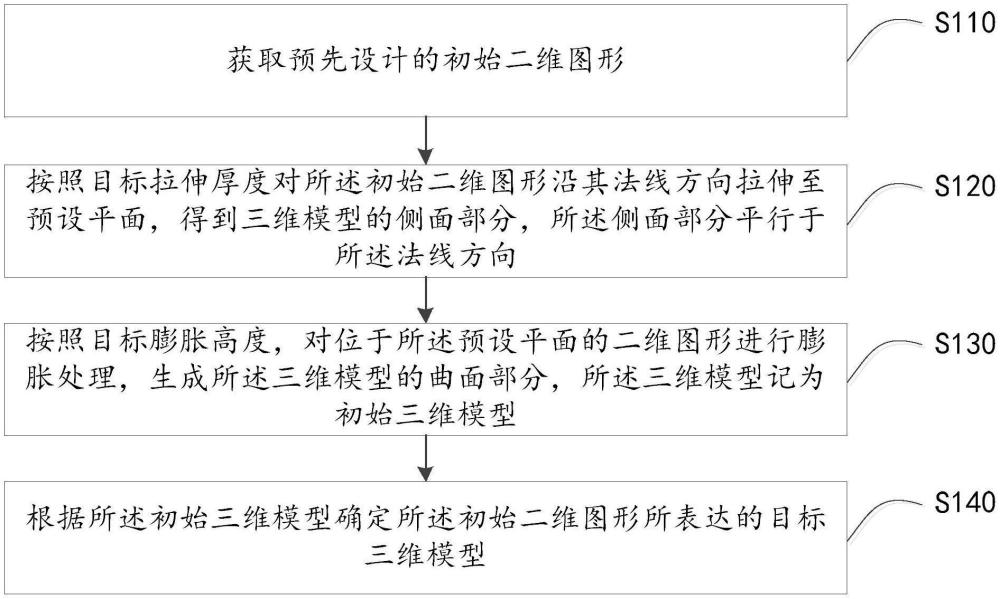
2、第一方面，本发明实施例提供一种三维重建方法，所述方法包括：

3、获取预先设计的初始二维图形；

4、按照目标拉伸厚度对所述初始二维图形沿其法线方向拉伸至预设平面，得到三维模型的侧面部分，所述侧面部分平行于所述法线方向；

5、按照目标膨胀高度，对位于所述预设平面的二维图形进行膨胀处理，生成所述三维模型的曲面部分，所述三维模型记为初始三维模型；

6、根据所述初始三维模型确定所述初始二维图形所表达的目标三维模型。

7、进一步地，所述初始三维模型的生成，包括：

8、以所述初始二维图形的中心点为原点，水平方向为x轴，垂直方向为y轴，法线方向为z轴，建立三维空间坐标系；

9、计算pxy到初始二维图形边界的有符号距离d，以及所述初始二维图形内部的坐标点到所述初始二维图形边界的最大距离dm，其中pxy表示三维空间中的坐标点p在xy平面的投影点；

10、根据所述目标拉伸厚度、所述目标膨胀高度、d和dm，生成所述初始三维模型的侧面部分和曲面部分。

11、进一步地，所述根据所述目标拉伸厚度、所述目标膨胀高度、d和dm，生成所述初始三维模型的侧面部分和曲面部分，包括：

12、将d和dm带入隐式曲面函数f(p)中，令f(p)＝0，求解方程，得到满足条件的三维坐标点，所述三维坐标点即构成了所述初始三维模型的侧面部分和曲面部分，其中所述隐式曲面函数基于二维椭圆方程逻辑对三维模型曲面部分进行定义；

13、所述f(p)为：

14、

15、其中，p.z表示p点的z坐标，h表示目标拉伸厚度，v表示目标膨胀高度，-h<p.z<h表示所述初始三维模型的侧面部分，p.z≤-h或p.z≥h表示所述初始三维模型的曲面部分。

16、进一步地，所述计算pxy到初始二维图形边界的有符号距离d，包括：

17、计算pxy到所述初始二维图形边界最近无符号距离值，记为d；

18、如果pxy在所述初始二维图形的内部，那么d＝-d，如果pxy在所述初始二维图形的外部，那么d＝d。

19、进一步地，所述根据所述初始三维模型确定所述初始二维图形所表达的目标三维模型，包括：

20、基于dua l-contour算法对所述初始三维模型进行曲面网格的提取，得到网格化的三维模型，记为过渡三维模型；

21、基于bi-lapl acian算子对所述过渡三维模型的曲面进行光滑处理，得到最终的目标三维模型，其中所述目标三维模型的曲面光滑，且与过渡三维模型曲面的形状一致。

22、进一步地，所述基于dua l-contour算法提取曲面的网格，得到网格化的三维模型，包括：

23、根据设定的分辨率，将三维模型的曲面内空间分成多个立方体；

24、计算立方体的8个顶点关于隐式曲面函数的值，如果计算的8个值中有大于0的，也有小于0的，则确定曲面与该立方体相交；

25、确定相交点在立方体中所属的边，计算共有该边的4个立方体的投影最小点，连接各立方体的投影最小点形成一个面片，所有面片构成了曲面的离散网格，即网格化的三维模型。

26、进一步地，所述基于b i-lap l ac i an算子对所述过渡三维曲面模型中的曲面部分进行光滑处理，得到最终的目标三维模型，其中所述目标三维模型的曲面光滑，且与过渡三维模型曲面的形状一致，包括：

27、将p.z>h的曲面部分和/或p.z<-h的曲面部分中的坐标点带入如下方程：

28、

29、其中，d是每个点的偏移量，其中△是lap l ac i an算子，d i v是散度算子，是梯度算子；

30、求解线性方程组，得到目标三维模型。

31、第二方面，本发明实施例还提供一种三维重建装置，所述装置包括：

32、图形获取模块，用于获取预先设计的初始二维图形；

33、初始生成模块，用于按照目标拉伸厚度对所述初始二维图形沿其法线方向拉伸至预设平面，得到三维模型的侧面部分，所述侧面部分平行于所述法线方向；按照目标膨胀高度，对位于所述预设平面的二维图形进行膨胀处理，生成所述三维模型的曲面部分，所述三维模型记为初始三维模型；

34、目标生成模块，用于根据所述初始三维模型确定所述初始二维图形所表达的目标三维模型。

35、进一步地，所述初始生成模块，包括：

36、坐标建立单元，用于以所述初始二维图形的中心点为原点，水平方向为x轴，垂直方向为y轴，法线方向为z轴，建立三维空间坐标系；

37、距离计算单元，用于计算pxy到初始二维图形边界的有符号距离d，以及所述初始二维图形内部的坐标点到所述初始二维图形边界的最大距离dm，其中pxy表示三维空间中的坐标点p在xy平面的投影点；

38、模型生成单元，用于根据所述目标拉伸厚度、所述目标膨胀高度、d和dm，生成所述初始三维模型的侧面部分和曲面部分。

39、进一步地，所述模型生成单元用于：

40、将d和dm带入隐式曲面函数f(p)中，令f(p)＝0，求解方程，得到满足条件的三维坐标点，所述三维坐标点即构成了所述初始三维模型的侧面部分和曲面部分，其中所述隐式曲面函数基于二维椭圆方程逻辑对三维模型曲面部分进行定义；

41、所述f(p)为：

42、

43、其中，p.z表示p点的z坐标，h表示目标拉伸厚度，v表示目标膨胀高度，-h<p.z<h表示所述初始三维模型的侧面部分，p.z≤-h或p.z≥h表示所述初始三维模型的曲面部分。

44、进一步地，所述距离计算单元用于：

45、计算pxy到所述初始二维图形边界最近无符号距离值，记为d；

46、如果pxy在所述初始二维图形的内部，那么d＝-d，如果pxy在所述初始二维图形的外部，那么d＝d。

47、第三方面，本发明实施例还提供了一种电子设备，包括：

48、至少一个处理器；以及

49、与所述至少一个处理器通信连接的存储器；其中，

50、所述存储器存储有可被所述至少一个处理器执行的指令，所述指令被所述至少一个处理器执行，以使所述至少一个处理器能够执行本发明实施例中任一项所述的方法。

51、第四方面，本发明实施例还提供了一种存储有计算机指令的非瞬时计算机可读存储介质，其中，所述计算机指令用于使所述计算机执行本发明实施例中任一项所述的方法。

52、第五方面，本发明实施例还提供了一种计算机程序产品，包括计算机程序，所述计算机程序在被处理器执行时实现根据本发明实施例中任一项所述的方法。

53、本发明实施例提供的技术方案，通过按照目标拉伸厚度对设计的初始二维图形进行拉伸至预设平面生成三维模型的侧面部分，按照目标膨胀高度对位于预设平面的二维图形进行膨胀处理，生成三维模型的曲面部分；然后根据生成的三维模型得到目标三维模型，从而实现根据用户的需求自动将二维图形转成它所表达的三维模型，并且用户可以根据需要进行目标拉伸厚度和目标膨胀高度的设定。

54、通过根据二维图形建立三维空间坐标系，然后基于设定的隐式曲面函数，根据初始二维图形边界的有符号距离、初始二维图形内部的坐标点到多边形的最大距离、目标拉伸厚度和目标膨胀高度，生成初始二维图形对应三维模型的侧面部分和曲面部分，最后根据三维模型的侧面部分和曲面部分确定初始二维图形最终的三维曲面模型，从而实现了自动将二维图形转成它所表达的三维模型。

55、此外，本发明实施例中的隐式曲面函数通过基于二维椭圆方程逻辑对三维模型曲面部分进行定义，使得生成的三维模型的曲面在最高点处是平行与基础平面的，在与基础平面的交接处是垂直于基础平面的，并且这个曲面在整体上还呈现一定的对称性，这种对称性即体现了二维平面图形本身的对称性，还在膨胀高度上体现由边界向中心的对称性。

56、在基于dua l-contour算法提取曲面的网格的过程中，通过确定相交点在立方体中所属的边，计算共有该边的4个立方体的投影最小点，连接各立方体的投影最小点形成一个面片，而非直接利用各立方体的中心点生成面片，本方案实施例方法可以使得提取的曲面网格更贴近多边形的实际形状。

57、本发明实施例的技术方案通过应用b i-lap l ac i an算子进行曲面部分的光滑处理，因为b i-lap l ac i an算子对曲面的高阶几何特征有更好的保持能力以及对曲率变化的敏感性，使得光滑处理后的曲面尽可能的与原始曲面的形状一致。