一种风机运行状态下塔架气动阻尼的解析方法

本发明属于风力发电机塔架，尤其涉及一种风机运行状态下塔架气动阻尼的解析方法。

背景技术：

1、随着风力发电技术的不断进步，风力机趋向大型化，其转子直径变大，轮毂变得更高。这一趋势导致风机结构具有更大的柔性，对风敏感性显著提升。塔架作为风机的关键支撑结构，其故障会导致严重的风机损坏甚至倒塌，可靠地预测塔架动态响应至关重要。

2、在风机动态响应预测中，阻尼是关键变量。风力机阻尼复杂多样，包括结构、气动、土壤及水动阻尼。其中气动阻尼因其多变性和巨大贡献，对风力机的动态响应影响显著。目前，主流的风力机气动弹性模拟软件(如openfast[1]、bladed[2]、hawc2[3])，通过非线性耦合空气动力-伺服-弹性时域模拟，隐式地包含了气动阻尼。这些非线性耦合模型虽然具有很高的精度，但计算过程耗时较长。在风力涡轮机的初步设计、疲劳和可靠性分析中，需要进行大量的计算。为解决计算成本问题，风机动态响应的快速计算(如频域分析、非耦合分析等)得到了发展。在快速计算中，准确确定气动阻尼成为了预测风机动态响应的关键。

3、传统的气动阻尼理论计算模型主要是基于经典叶素动量理论建立的[4,5]。随后，不少学者在此基础上发展了气动阻尼的半解析模型，以计算刚性转子假设下顺风向和横风向的气动阻尼[6-8]。尽管近些年来也有些学者在气动阻尼理论模型中考虑叶片柔性下的影响[9,10]，但在气动阻尼耦合模型中仍然亟需同时考虑叶片柔性、塔顶旋转、结构振动对诱导因子的影响以及修正的叶素动量理论。这不仅提高了气动阻尼的计算精度，而且有助于深入了解气动阻尼。

4、因此，如何实现对运行状态下风机塔架气动阻尼的准确计算，是本领域技术人员目前需要解决的技术问题。

5、参考资料：

6、[1]jonkman jm,buhl jml.fast user's guide-updated august 2005.unitedstates2005.

7、[2]bossanyi ea.gh bladed theory manual.:gh&partners ltd,2003.p.56-8.

8、[3]juul larsen,t,melchior hansen,a.how 2hawc2,the user'smanual.denmark2007.

9、[4]garrad ad.forces and dynamics of horizontal axis windturbines.wind energy conversion systems；freris,ll,ed.；prentice hall:new york,ny,usa.1990119-42.

10、[5]van der tempel j.design of support structures for offshore windturbines:published and distributed by the author,2006.

11、[6]valamanesh v,myers at.aerodynamic damping and seismic response ofhorizontal axis wind turbine towers.j struct eng.2014；140.

12、[7]liu x,lu c,li g,godbole a,chen y.effects of aerodynamic damping onthe tower load of offshore horizontal axis wind turbines.appl energ.2017；2041101-14.

13、[8]chen c,duffour p,fromme p.modelling wind turbine tower-rotorinteraction through an aerodynamic damping matrix.j soundvib.2020；489.

14、[9]chen y,di wu,yu y,gao w.an improved theory in the determination ofaerodynamic damping for a horizontal axis wind turbine(hawt).j wind eng indaerod.2021；213.

15、[10]zhang z,hammad ka,song y.closed-form derivation of aerodynamicdamping matrix and pitch vector of an aero-servo-elastic wind turbinesystem.j wind eng ind aerod.2023；238.

16、[11]jonkman j,butterfield s,musial w,scott g.definition of a 5-mwreference wind turbine for offshore system development.:national renewableenergy lab.(nrel),golden,co(united states),2009.

17、[12]commission ie.wind energy generation systems-part 3-1:designrequirements for fixed offshore wind turbines.international standardiec.201961400-3.

技术实现思路

1、为了克服现有技术的不足，本发明提供一种风机运行状态下塔架气动阻尼的解析方法。

2、本发明的一种风机运行状态下塔架气动阻尼的解析方法，包括以下步骤：

3、步骤1：风机模型的构建。

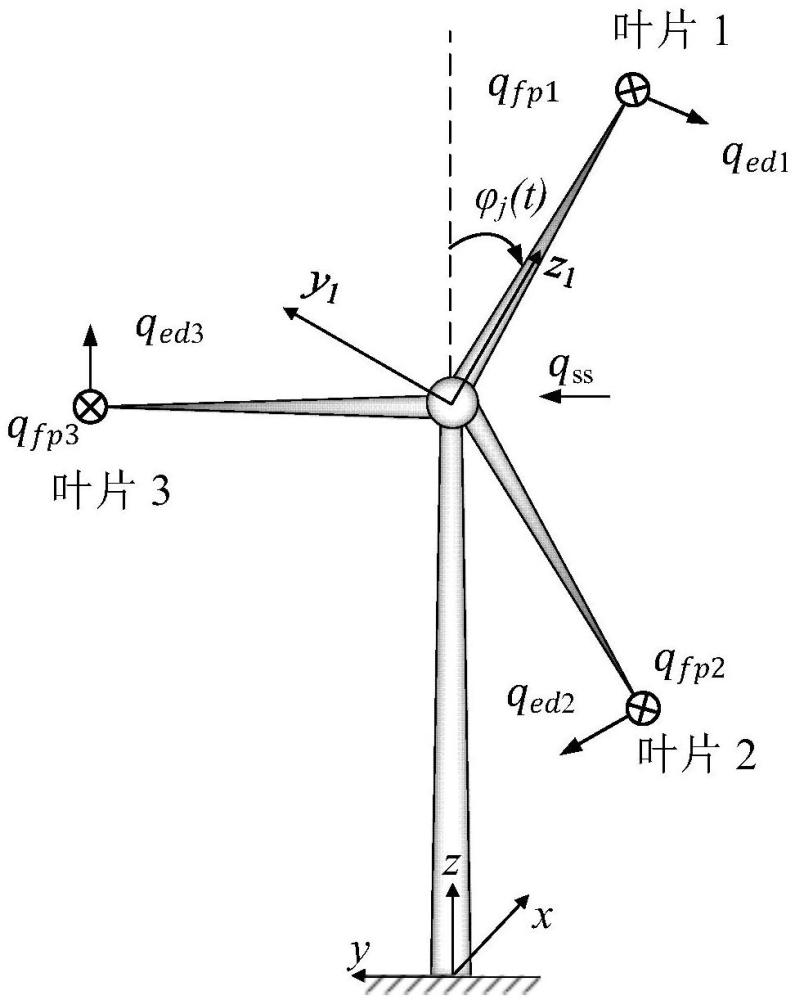
4、采用整体坐标系和叶片截面坐标系描述风机的运动；风机由叶片、轮毂、机舱和塔筒组成；风机的运动由8个自由度来定义；三个叶片挥舞和摆振方向上的运动分别用自由度qfpj和qedj，j＝1,2,3来表示；塔筒的运动由x和y方向上的平动自由度qfa和qss来表示；叶片的旋转角速度为ω(t)；叶片的方位角为基于风机塔架和叶片各个部件的运动，得到风力机的动能和势能，并结合欧拉拉格朗日方程，求得风机的时变质量矩阵m，结构阻尼矩阵c，时变刚度矩阵k。

5、步骤2：非线性气动力线性化。

6、基于修正的叶素动量理论，非线性气动荷载fn,j(r,t)正向力和ft,j(r,t)切向力将在风速v0和vr附近通过一阶泰勒展开，获得线性气动荷载：

7、

8、式中，和分别为风轮平面外和平面内风速为v0和vr的正向力和切向力；和分别为正向力对风速v0和vr的偏导；和分别为切向力对风速v0和vr的偏导；和分别为叶片在x1和y1上的振动。

9、在风速v0和vr下正向力和切向力为：

10、

11、其中，为相对合速度的均值，和分别为风速v0和vr下的正向力系数和切向力系数；和分别为风速v0和vr下的轴向和切向诱导因子，由修正的叶素动量理论迭代得到。

12、偏导数和的推导是基于变量v0和vr的结果：

13、

14、其中，和分别为合速度对风速v0和vr的偏导；和分别为正向力系数对风速v0和vr的偏导；和分别为切向力系数对风速v0和vr的偏导。

15、步骤3：气动阻尼矩阵的推导。

16、基于虚功原理和线性化气动荷载，广义力气动荷载可以表示成：

17、

18、其中，为不考虑结构振动下的风荷载，ca为气动阻尼矩阵，表示为：

19、

20、步骤4：多叶坐标变换。

21、利用多叶片坐标变换将所有动态变量映射到固定坐标系中，去除状态矩阵中的周期项；多叶片坐标变换即mbc变换包括两个步骤：旋转自由度的变换和运动方程的变换。

22、通过变换矩阵tf，叶片自由度从旋转系统变换到固定系统：

23、pi＝tfqi,i＝e,f       (9)

24、其中，qi为旋转坐标系的自由度，pi为固定坐标系下的新自由度；tf表示为：

25、

26、其中，

27、基于mbc变换，风力机的一阶状态空间运动方程表示为：

28、

29、其中，可看出a0和b0是时不变的，可直接对系统进行复特征值分析。

30、步骤5：复特征值分析，求解气动阻尼。

31、方程的齐次解以如下形式得到：y(t)＝re(ψλt)；通过求解以下方程得到：

32、

33、其中，λk为第k阶的特征值；ωk和ξk分别为第k阶的自振频率和阻尼比；为第k阶的阻尼频率；模态自振频率通过复数根λk的绝对值来获得，模态阻尼比从复数根λk中获得：

34、

35、最后通过求解复特征值问题得到不同风速在固定坐标系下的模态自振频率和气动阻尼比。

36、本发明的有益技术效果为：

37、本发明在气动阻尼耦合模型中综合考虑了叶片柔性、塔顶旋转、结构振动对诱导因子的影响以及修正的叶素动量理论。实现了运行状态下风机塔架气动阻尼的准确计算，有助于深入了解气动阻尼。