多模态旅行商问题的优化方法

本发明涉及路径规划，尤其是涉及一种多模态旅行商问题的优化方法。

背景技术：

1、tsp(traveling salesman problem，旅行商问题)是一个经典的组合优化问题，最早由数学家哈斯卡尔·哈斯卡尔和托马斯·柯克曼在19世纪提出。它的基本概念是：给定一组城市和它们之间的距离(或成本)，找到一条路径，使得每个城市恰好访问一次，并最终回到起点，使得路径总长度最小。tsp是组合优化理论中的经典问题，涉及到图论、算法设计和计算复杂性理论等多个数学和计算机科学领域，它代表了np-hard问题的一个重要类别，即使在相对较小的问题规模下，也需要大量计算来找到最优解，这意味着随着城市数量的增加，找到最优解的计算复杂性呈指数级增长。近年来，启发式算法在解决tsp中表现出色，如贪婪算法、遗传算法、模拟退火算法、蚁群算法和粒子群算法等，这些算法通过模拟生物或物理系统的行为，以找到解决方案的优化路径，在不同的场景和问题规模下这些算法表现出各自的优势。

2、随着计算能力的提升和算法研究的进展，tsp的应用场景越来越广泛和复杂。主要体现在路径规划和资源优化的领域，如：在物流管理中，经常需要规划送货员或运输车辆的最优路径，以尽量减少时间或成本，tsp可以帮助优化每日送货路线，使得配送效率最大化，减少里程和运输成本；在芯片设计中，tsp被用来优化电路板上的连接路径，以最小化信号传输的延迟和能耗，通过寻找最优路径，可以提高电路的性能和可靠性；在无人机应用中，tsp可以帮助规划无人机的飞行路径，以最小化能耗或完成多个目标点的任务，这种优化对于无人机在农业、勘探和救援等领域的应用尤为重要。通过提高资源利用效率和决策制定的科学性，tsp的研究为现实生活中的各个领域带来了显著的价值和成果。

3、大多数tsp相关问题和tsp变体关注于找到一个最优解决方案，而不考虑可能存在多个高质量解决方案的事实。然而，在现实生活中，向决策者提供各种最佳备选方案，以便在紧急情况下能够迅速采取另一种方案，例如由于城市道路工程造成的交通拥堵或由于恶劣天气而取消航班等，由于不同的路线选择，也可以平衡交通负荷，因此这一需求催生了多模态旅行商问题的研究。多模态旅行商问题的研究不仅在理论上有重要意义，更在实际应用中对优化效率、降低成本、提供更多灵活高效的解决方案等方面产生深远影响。

技术实现思路

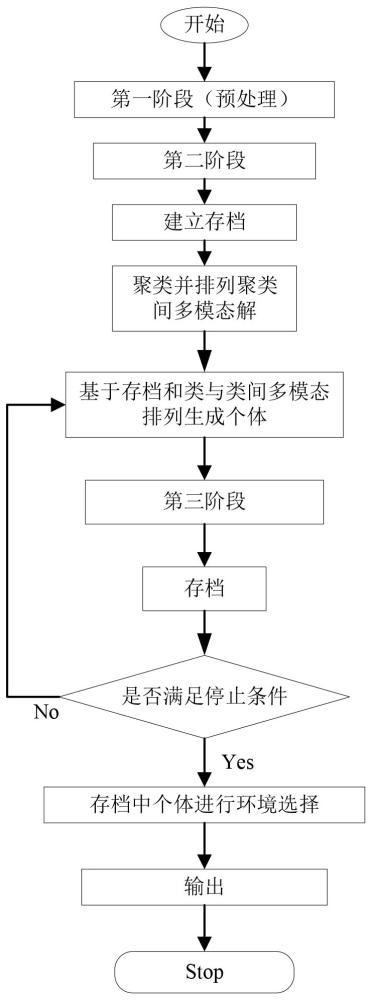
1、本发明在传统tsp上对其多模态性进行了深入研究，基于多模态旅行商问题为背景，提供了一种“预处理-全局收敛-局部寻优”的分阶段优化方法，该优化方法可以在找到最优值的同时，提供多个多模态解决方案，以满足不同用户的偏好和需求。

2、本发明采用的技术方案为：

3、多模态旅行商问题的优化方法，包括以下步骤：

4、步骤1，对解进行初步寻优；

5、步骤2，基于步骤1得到关键边集，采用两种个体生成策略对解进行快速的全局收敛，采用环境选择策略对多模态解删除或保留；

6、步骤3，基于目标空间距离自适应生成聚类，根据聚类个数排列类间多模态解；基于存档和类间多模态排列生成个体，并基于跳跃算子的局部搜索策略，对个体进行局部寻优。

7、进一步，在步骤1具体为：

8、步骤1.1，根据问题规模初始化种群，种群大小为np，对种群个体进行适应度值计算；

9、步骤1.2，对初始种群进行交叉操作以产生后代，计算适应度值；

10、步骤1.3，将父代与子代合并进行环境选择；

11、步骤1.4，在达到停止条件前循环迭代。

12、进一步，在步骤1.2中，对交叉操作包括以下步骤：

13、步骤1.2.1，根据问题规模初始化种群，

14、步骤1.2.2，随机选择两个父代：

15、p1＝3 5 6 7 8 9 2 1 4

16、p2＝4 7 3 1 2 5 6 8 9

17、步骤1.2.3，随机生成两个交点将个体分为三段，并在子代中留下中间部分：

18、p1＝3 5 6|7 8 9 2|1 4

19、p2＝4 7 3|1 2 5 6|8 9

20、o1＝***|1 2 5 6|**

21、o2＝***|7 8 9 2|**

22、步骤1.2.4，留下交点中间部分并将其放在第三段：

23、p1＝1 4|3 5 6|7 8 9 2

24、p2＝8 9|4 7 3|1 2 5 6

25、步骤1.2.5，从父代2中删除父代1的中间部分得到4-3-1-5-6，从父代1中删除父代2的中间部分得到4-3-7-8-9，补充得到子代：

26、o1＝7 8 9|1 2 5 6|4 3

27、o2＝1 5 6|7 8 9 2|4 3

28、进一步，在步骤2具体为：

29、步骤2.1，步骤1预处理后的种群根据其适应度值排列，结合关键边集和贪婪策略采用两种个体生成策略，同时种群仍进行交叉操作，个体产生多子代；

30、步骤2.2，将子代合并，去除冗余个体，以避免计算资源的浪费，计算子代适应度值；

31、步骤2.3，将父代与子代合并进行环境选择，采用环境选择机制对多模态解进行删除和保留；

32、步骤2.4，步骤2循环采用两种停止条件：

33、(1)整个种群最优值迭代次仍未更新，将结束步骤2的循环；

34、(2)达到设置的步骤2最高评价次数。

35、进一步，在步骤2.1中，所述关键边和关键边集的概述具体为：

36、关键边：在种群中较好个体(包含多模态解)的不同路径方案中，某部分城市的连接顺序相同即在个体中存在相同的基因片段；

37、关键边集：在不同目标值的所有多模态解或同一目标值下的多模态解中可识别多条不同的关键边，所有关键边的集合称为关键边集；若可以成功识别关键边集就可以适当减小搜索空间，实现一定程度的降维。

38、进一步，在步骤2.1中，两种个体生成策略包括以下步骤：

39、步骤2.1.1，对整个种群按照适应度值排序，识别排名前4的所有个体(包括多模态解)中的关键边集并标记关键边出现次数，认为出现次数越多该关键边的重要程度越高；

40、步骤2.1.2，第一种个体生成策略：关键边维度固定为总城市维度的四分之一，按照步骤2.1.1识别并标记关键边次数后，基于次数的重要性生成个体，关键边的每次出现都生成一个个体，一个个体的四分之一为关键边维度，关键边的识别至少为3条边才有意义，3条边需要4个城市顶点才可以确定，因此，若关键边维度算出小于4则将关键边维度设为4，其余部分将随机插入其余位点，并保证个体基因染色体位点不重复即个体为有效解；

41、步骤2.1.3，第二种个体生成策略核心在于贪婪策略和次数的结合，步骤2初始关键边维度为总城市维度的五分之一，随迭代的进行更新关键边维度，具体操作为每50代关键边维度增加2，直至关键边维度为总城市维度的三分之二停止更新。

42、仍按照步骤2.1.1识别并标记关键边次数后，对于没有重复基因的两条关键边，组合生成两个个体，具体步骤为：

43、(1)第一个个体：将其中关键边1放入最前端，在没有基因位点的位置随机生成一个位点放入另一条关键边2，空余位点将按照贪婪策略补充；

44、(2)第两个个体：将两条关键边逆转，将逆转后的关键边2放入最前端，随机生成一个位点放入逆转的关键边2，空余位点将按照贪婪策略补充；

45、对于其余识别的不能组合的关键边，仍生成两个个体，具体步骤为：

46、(1)第一个个体：将关键边放入最前端，空余位点将按照贪婪策略补充；

47、(2)第两个个体：将关键边逆转放入最前端，空余位点按照贪婪策略补充；

48、步骤2.1.4，上述两种个体生成策略针对整个种群排名前4的个体，因此具有较强的收敛速度，对于整个种群仍需要进行交叉操作。

49、进一步，在步骤2.2中，所述冗余个体为：

50、上述步骤2.1中两种个体生成策略和交叉操作生成三部分子代，其中两种个体生成策略并不控制其生成子代数量，因此子代合并后可能出现重复个体、回环个体和倒序个体，将其定义为冗余个体，在计算适应度值之前进行去重操作，以避免资源的浪费。

51、其中，回环个体即在tsp求解问题中，目标值的计算就是一个回路距离计算，例如个体1-2-3-4-5-6和个体5-6-1-2-3-4，在实际情况下是同一个体；倒序个体例如个体1-2-3-4-5-6和个体6-5-4-3-2-1，在不考虑先后顺序的情况下仍是同一个体，但在实际情况下若顾客对城市先后顺序有要求也可作为一种多模态解，在本文中将其作为了冗余个体去除。

52、进一步，在步骤2.3中，环境选择包括以下步骤：

53、步骤2.3.1，对整个种群按照适应度值排序，由于不控制种群数量，因此首先预保留1.4*np个个体进行环境选择；

54、步骤2.3.2，将同一目标值下的个体即多模态解聚类，直接保留排名为1的所有个体，其余个体将按照种群大小np分配；

55、步骤2.3.3，同一目标值下的多模态解个数为1或2的个体直接保留，超过2的将根据以下公式保留一定的数量：

56、

57、其中，cn为当前聚类数量，np为种群大小。

58、步骤2.3.4，根据上述计算的保留个数，根据个体的相似度进行多模态解的保留和删除，保留一个相似度最差的，其余保留相似度好的。

59、为衡量解决方案之间的相似性，将利用解之间的共有边个数n1和按相同顺序访问的顶点数n2，对于有n维城市的两个解x1＝(x11,x12,…,x1n,x11)和x2＝(x21,x22,…,x2n,x21)，n1和n2由以下公式计算：

60、n1＝|φ(x1)∩φ(x2)|

61、其中，φ(x1)和φ(x2)分别为解x1和x2的边；

62、

63、其中，若x1i＝x2i，则ki＝1，否则ki＝0；

64、个体的相似度可理解为解在决策空间的距离，解之间的相似度由以下公式计算：

65、

66、其中，s(x1,x2)的值在0到1之间。n1和n2的值越大，s(x1,x2)值越小，也就意味着两个解越相似，当s(x1,x2)＝0时，解相同。

67、进一步，在步骤2.4中，对停止条件的最高评价次数和停滞代数具体设置为：

68、对于问题mstsp1-mstsp12，最高评价次数设为60000，步骤1最高评价次数设为3000，步骤2最高评价次数设为20000，由于步骤3一次循环最多生成1500个子代，因此步骤3的停止条件设为58000；

69、对于问题mstsp13-mstsp25，最高评价次数设为1200000，步骤1最高评价次数设为15000，问题mstsp13-mstsp25最低维度为22，最高维度为66，低维问题的难度在于其多样性，高维问题的难度在于其收敛性和多样性，为合理利用计算资源，在城市维度大于22且小于45时，将步骤2的最高评价次数设为200000，停滞代数设为80；在城市维度大于等于45且小于60时，将步骤2的最高评价次数设为300000，停滞代数设为100；在城市维度大于等于60时，将步骤2的最高评价次数设为400000，停滞代数设为150。由于步骤3一次循环最多生成1500个子代，因此步骤3的停止条件设为1198000。

70、对于停止条件的设置，用户可根据实际情况和计算资源自行设置。

71、进一步，在步骤3具体为：

72、步骤3.1，建立存档，将上述步骤2环境选择后的所有个体保存进存档内；

73、步骤3.2，选择存档中的最佳个体，利用最佳个体的目标空间距离自适应生成聚类；

74、步骤3.3，根据上述步骤的聚类个数全排列类间多模态解，去除聚类间回环和倒序的无效排列得到所有可能的有效排列；

75、步骤3.4，利用平均值求聚类中心，并根据上述的有效排列求聚类中心之间的回路距离，将类与类之间顺序按照重要程度排列，为保证每种排列循环的有效性，在一定计算资源内保证重要顺序的计算资源，将保留最多三种排列，用户可根据实际情况和计算资源更改；

76、步骤3.5，基于存档和类间多模态排列生成个体，进入循环迭代寻优；

77、步骤3.6，在问题mstsp1-mstsp12中，步骤3进化从种群的排名前3的个体中识别关键边集。在问题mstsp13-mstsp25中，步骤3进化前期从种群的排名前8的个体中识别关键边集，在进化后期从排名前3的个体中识别关键边集，关键边的识别操作同上述步骤2，关键边维度为随机整数；

78、步骤3.7，进化后期整个种群趋于稳定，因而个体与个体之间相似度极高，所识别的关键边集相似度也极高，在利用关键边之前进行冗余关键边的去重；

79、步骤3.8，随迭代进化，种群收敛程度较高，一个个体可能出现多个关键边，从而生成后代个体数量巨大，因此设置生成个体上限，对每个个体的搜索资源按比例分配。随后再对识别到关键边的个体进行基于跳跃算子的局部搜索策略，对生成个体进行冗余个体的去重和环境选择；

80、步骤3.9，对上述得到的个体进行交叉操作和两种不保护关键边集的局部突变操作，合并父代和子代个体去重并进行环境选择，保存进存档；

81、步骤3.10，每种类间排列得到的种群均放入存档内，对存档内所有个体进行环境选择并输出。

82、对于问题mstsp1-mstsp12，最高维为15，在此低维问题中将不进行上述步骤3.2到步骤3.5。

83、进一步，在步骤3.2中，基于目标空间距离自适应生成聚类的具体步骤如下：

84、步骤3.2.1，选择存档中的最佳个体，计算每个城市与城市之间的距离形成一个1行n列矩阵，并计算个体目标值，用以下公式求城市间距离平均值：

85、mean＝sum/n

86、其中，sum为个体目标值，n为城市维度；

87、步骤3.2.2，从1行n列矩阵元素中识别大于mean的个数就是聚类个数，将个体与矩阵对应可得到聚类。

88、进一步，在步骤3.5中，基于存档和类间多模态排列生成个体具体步骤如下：

89、步骤3.5.1，将存档内的个体按照上述的聚类方法逐个分段聚类，每个类按顺序标记；

90、步骤3.5.2，按照步骤3.4的所有排列方式依次循环进入局部搜索，基于存档和类间多模态排列有三种个体生成的方式：

91、(1)按照排列顺序依次组成个体；

92、(2)先放入第一个聚类的基因片段，分别计算第一个基因片段的最后一位基因与第二个聚类的第一位和最后一位的距离，若与第二个聚类的第一位距离更短则直接放入第二个聚类，否则若与第二个聚类的最后一位距离更短则将第二个聚类的基因片段整个逆转后再填充入个体，其余聚类的基因片段同此操作依次放入；

93、(3)利用回环原理，将第一个聚类的基因片段放入空白个体的最后，分别计算填充后个体的有效片段第一个位点与最后一个聚类的基因片段的第一位和最后一位的距离，按照上述方式连接最短的一段。

94、按照上述方式，存档内一个个体将生成3个子代，将子代合并并去重后进行进行环境选择。

95、进一步，在步骤3.6中，随机选择关键边维度的具体设置如下：

96、(1)对于问题mstsp1-mstsp12，关键边的识别至少为3条边才有意义，3条边需要4个城市顶点才可以确定，因此，关键边维度的范围选择最低为4，关键边维度的随机选择范围为：

97、ceslen∈(4,n-5)

98、其中，n为城市维度。

99、(2)对于问题mstsp13-mstsp25，其最低维度为28，最高维度为66，对于城市维度大于45的问题，初始关键边维度将设为问题规模的三分之一，其余问题将设置为四分之一，关键边维度的随机选择范围下限将随着迭代进化而线性增加，即每80代增加4，上限则设置为n-5。

100、进一步，在步骤3.8中，基于跳跃算子的局部搜索策略为：

101、对每个个体进行识别关键边集并标记关键边出现次数，对个体的局部搜索将保护关键边所在的基因片段，即该部分基因片段将直接继承给后代，随机选择相邻的基因片段，对该片段上的基因位点进行随机的突变调换，由于此时个体已经趋于稳定，因此随机突变调换的基因片段维度不可太多，其余位点也直接继承给后代。

102、上述随机选择基因片段进行染色体的突变将根据标记的关键边出现次数进行多次，一个个体可能出现多个关键边，从而生成后代个体数量巨大，因此设置生成个体上限，对每个个体的搜索资源按比例分配。

103、进一步，在步骤3.9中，随迭代进化，种群收敛程度较高，基于关键边集的个体可能陷入局部最优，为跳出局部最优，在不保护关键边集的情况下对个体进行两种局部突变操作：

104、(1)局部突变操作：局部突变操作采用步骤3.8相同原理，其不同的是这里的局部突变不再保护关键边，即随机选择相邻的基因片段包含关键边时仍对其进行突变调换，其余基因片段直接继承给子代；

105、(2)局部逆转突变操作：仍在不保护关键边的情况下在个体上随机选择两个染色体，将两个染色体中间的片段进行逆转。

106、对于以上两种变化，随机选择的基因片段维度设为10以内，太大范围的变动是无意义的。

107、本发明在指标计算时用到两个指标。评价指标的具体信息如下：

108、

109、其中，fβ反映了得到解的质量即收敛性p反映了准确率，其中tp为算法得到的解中为最优解的个数，fp为算法得到解中非最优解的个数，fn是算法漏掉的最优解个数。

110、本发明所具有的有益效果为：

111、1、本发明对旅行商问题从“预处理-全局收敛-局部寻优”三个阶段提出了一种多模态旅行商问题的优化方法；在全局收敛阶段，认为关键边次数出现越多则越重要，基于此提供了两种个体生成策略，减小了整个种群的搜索空间，使得整个种群进行一个快速得收敛；同时，提出了冗余个体概念，避免在搜索过程有不必要的资源浪费，最后，针对多模态解的保留和删除提供了一种新的环境选择策略，为跳出局部最优，保留了部分非精英个体，在不损失收敛性的同时一定程度上增强了多样性。

112、2、本发明利用上述全局收敛阶段得到的最佳个体进行基于目标空间距离自适应生成聚类操作，个体聚类得到聚类个数，对聚类个数进行排列，得到聚类中心的回路距离，将类与类之间顺序按照重要程度排列，为了在有效资源内保证重要的类间排列多模态解，留下最有希望的类与类间的排列；同时，采用了一种基于存档和类间多模态排列的个体生成策略，对存档内个体进行类间排列的重组。

113、3、本发明在基于上述的个体生成对整个种群进行局部寻优，这一阶段可以寻找到更多多模态解；对整个种群的最好个体识别关键边并标记次数，仍认为关键边的出现次数越多则越重要，随后清除冗余的关键边，基于此提出了一种基于跳跃算子的局部搜索策略，该策略在保护关键边的基础上大范围搜索多模态解生成大量子代，对子代进行去重和环境选择后进行交叉突变，为避免种群进入局部最优，采用了两种不保护关键边的局部突变操作。

114、4、由于高维问题的复杂性，本发明能够相较于其他算法提供更多的多模态解，为决策者提供更灵活的选择。