一种基于动态约束的对称非均匀FDTD网格生成方法与流程

本发明涉及仿真设计领域，具体涉及一种基于动态约束的对称非均匀fdtd网格生成方法。

背景技术：

1、时域有限差分法（fdtd，finite difference time domain）是电磁场数值计算的重要方法之一，该方法采用中心差商代替场量对时间和空间的偏微分，进而在时域内递推模拟电磁场的传播过程，从而得出场分布。作为一种时域方法，fdtd运算方法可以在一次模拟运行时同时计算多个频率范围，并且可以自然地处理各种线性材料特性。

2、中国专利cn105279320a公开了一种生成fdtd网格的方法，该方法通过将模型剖分成三角面元，再转换成fdtd网格。在fdtd方法中，迭代计算是在六面体网格上进行的，这些网格可以是均匀的或非均匀的。如图3a和图3b所示，均匀网格的特点是所有网格单元尺寸相同，而非均匀网格的单元尺寸则各不相同。其中，非均匀网格能够更好地适应模型的具体形状，但同时也可能引入数值色散，导致仿真结果的不稳定。

3、本发明旨在解决非均匀网格可能带来的稳定性问题。

技术实现思路

1、为了解决上述问题，本发明提出了一种基于动态约束的对称非均匀fdtd网格生成方法，该方法保证网格在满足其他非对称网格约束的基础上，还保证关于模型中心对称的。

2、本发明提出了一种基于动态约束的对称非均匀fdtd网格生成方法，包括：

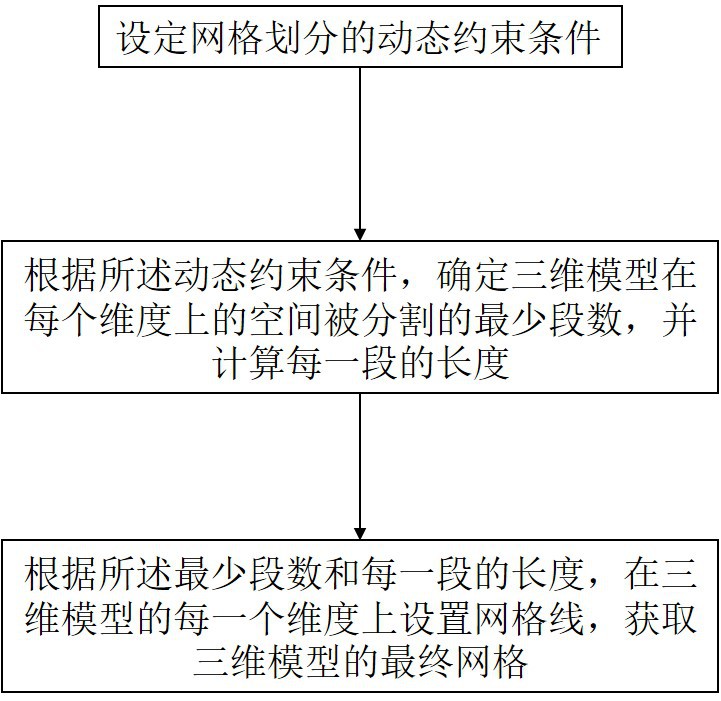
3、设定网格划分的动态约束条件；

4、根据所述动态约束条件，确定三维模型在每个维度上的空间被分割的最少段数，并计算每一段的长度；

5、根据所述最少段数和每一段的长度，在三维模型的每一个维度上设置网格线，获取三维模型的最终网格，所述最终网格为对称非均匀fdtd网格，所述最终网格满足动态约束条件且拥有最少网格数量。

6、在一个实施例中，三维模型在每个维度上的空间被分割成多段，每个网格对应一个段，在同一个维度上，所述动态约束条件包括：

7、每个网格的长度不小于最小网格常数；

8、每个网格的长度不大于最大网格常数；

9、位置互相对称的两个网格的长度相等；

10、相邻两个网格的比值在预设范围内；

11、位于两端的网格的长度等于最小网格常数。

12、在一个实施例中，令三维模型在一个维度上的空间总长度为l，将总长度为l的空间分割成n段，每段长度为li；

13、所述每个网格的长度不小于最小网格常数为：li≥minsize；

14、所述每个网格的长度不大于最大网格常数为：li≤maxsize；

15、所述位置互相对称的两个网格的长度相等为：li=ln-1-i；

16、所述相邻两个网格的比值在预设范围内为：，0<i<n；

17、所述位于两端的网格的长度等于最小网格常数为：l0=ln-1=minsize；

18、所述确定三维模型在每个维度上的空间被分割的最少段数为：n= min{n | n满足动态约束条件}；

19、其中，minsize为最小网格常数，maxsize为最大网格常数，r为大于1的比例常数ratio，l为一个维度上的空间总长度，n为一个维度上空间被划分的段数，n为最少段数，i为段号，0≤i＜n。

20、在一个实施例中，所述三维模型在每个维度上的空间被分割的最少段数的求解方法，包括如下步骤：

21、步骤11，令段数n为n的最小可能值；

22、步骤12，判断n是否小于n的最大可能值，若是则进入步骤13，否则求解失败；

23、步骤13，求解段数n，若有解，则求解成功，否则，令n=n+1并返回步骤12；

24、其中，所述步骤11中，n的最小可能值的获取方法为：将总长度l除以最大网格常数maxsize的结果向上取整；

25、所述步骤12中，n的最大可能值的获取方法为：将总长度l除以最小网格常数minsize的结果向下取整。

26、所述步骤13中，求解段数n为：判断n是否满足动态约束条件。

27、在一个实施例中，所述计算每一段的长度，包括：计算nhalf个段长度，n为奇数或偶数时，nhalf =；

28、所述计算nhalf个段长度，包括：构建段长度计算函数来计算nhalf个段长度，所述段长度计算函数包括：

29、若n为奇数，在满足动态约束条件的情况下求解下式（1）：

30、（1）；

31、若n为偶数，在满足动态约束条件的情况下求解下式（2）：

32、（2）。

33、在一个实施例中，所述计算nhalf个段长度，包括：

34、将待求解的nhalf个段长度分为两段：nv个可变长度段和nhalf-nv个固定长度段，所述固定长度段的长度均为maxsize；

35、求解nv个可变长度段的具体长度：求解可变长度段的数量nv的最小值minvariablen，利用minvariablen对nv进行遍历，求解nv个可变长度段的具体划分情况。

36、在一个实施例中，所述求解可变长度段的数量nv的最小值minvariablen，包括如下步骤：

37、步骤21，初始化网格总长度lsum、最小网格常数minsize和minvariablen的值：将网格总长度lsum初始化为最小网格常数minsize，将当前网格段长度l初始化为最小网格常数minsize，将可变长度段的数量nv的最小值为minvariablen初始化为1，所述网格总长度lsum为到目前为止所有可变长度段的总长度；

38、步骤22，如果当前网格段长度l小于maxsize，并且网格总长度lsum小于一个维度上的空间总长度的一半l/2，则执行步骤23，否则结束并返回minvariablen；

39、步骤23，如果minvariablen=nhalf且n为奇数，则更新网格段长度l为（l*ratio）/2，并进入步骤24，否则更新网格段长度l为l*ratio，并进入步骤24；

40、步骤24，更新网格总长度lsum的值为当前网格总长度加上当前网格段长度l，更新可变长度段的数量nv的最小值minvariablen为当前最小值minvariablen加一，并返回步骤22继续进行迭代。

41、在一个实施例中，所述利用minvariablen对nv进行遍历，求解nv个可变长度段的具体划分情况，包括如下步骤：

42、步骤31，将可变长度段的数量nv初始化为minvariablen；

43、步骤32，判断nv是否小于n，若是，则进入步骤33，否则求解失败；

44、步骤33，求解nv个可变长度段的具体划分情况；

45、步骤34，判断是否有解，若有解则求解成功，否则将可变长度段的数量nv加一以更新可变长度段的数量nv，并返回步骤32继续进行迭代。

46、在一个实施例中，所述步骤33中，求解nv个可变长度段的具体划分情况，具体包括如下步骤：

47、步骤331，将i初始化为nv；

48、步骤332，判断所有可变长度段的长度lm是否都是不可更新状态，其中，0≤m＜nv，若否，则进入步骤333，若是，则求解失败；

49、步骤333，判断i是否小于0，若是，则更新i为nv，并返回步骤332重新开始循环，否则进入步骤334；

50、步骤334，判断当前的段长度li是否能够更新，若否，则将i减一以更新i，并返回步骤332；若是，则进入步骤335；

51、步骤335，利用牛顿法求解方程更新当前的段长度li至新的值ltemp，并对ltemp施加约束，所述牛顿法求解方程为，其中，fc表示段长度计算函数中的fe或f0；

52、步骤336，判断li是否等于ltemp，若是，则标记lm为不可更新，将i减一以更新i，并返回步骤332，否则，进入步骤337；

53、步骤337，更新li为ltemp，将所有lm标记为可更新；

54、步骤338，判断是否求解成功，所述求解成功为li满足所述段长度计算函数，若是，则求解成功，否则将i减一以更新i，并返回步骤332继续迭代。

55、在一个实施例中，所述步骤335中，对ltemp施加约束中的约束值的计算方法为：

56、，0＜i＜nv；

57、，i=0；

58、，0≤i＜nv-1；

59、，i=nv-1；

60、其中，所述为第i个可变长度段长度的最小值，为第i个可变长度段长度的最大值，所述ratio为比例常数；

61、所述步骤335中，对ltemp施加约束的过程为：

62、；

63、以及，；

64、其中，0≤i＜nv。

65、本发明的一种基于动态约束的对称非均匀fdtd网格生成方法的有益效果在于：

66、1、优化仿真结果与网格生成效率：

67、现有fdtd网格自动生成算法中采用线性递增或递减的方法生成对称网格，本发明能够确保在对称结构模型上取得最优的仿真结果。对称网格的生成不仅提高了仿真的精度，而且由于网格与模型结构的良好匹配，也减少了网格数量，从而提高了仿真效率。

68、2、动态约束与算法稳定性：

69、在迭代过程中，本发明对待求变量使用动态约束，并解耦变量之间的约束依赖，这使得求解过程更加灵活和高效。数学理论的完备性，只需求解线程方程，且具有非0常量一阶微分，数值误差小，保证了求解过程中的稳定性和高效性。算法简单易于实现和维护，使得整个过程既稳定高效，又便于理解和操作。

70、3、灵活的牛顿迭代与网格优化：

71、本发明在牛顿迭代中，求解方程和计算微分的方程不同。针对划分段数为奇数和偶数的情况使用不同的方程，特别是对于奇数情况下的最后一项采用其二分之一求和的处理方法，而保持微分公式不变，这样在更新变量li时可以进行一致的处理。此外，通过使用渐变算法并最大程度地使用更多的最大网格尺寸，既减少了网格数量，提高了仿真效率，同时又增强了仿真的稳定性，从而在整体上提升了算法的性能。