一种阵列式MEMS陀螺仪高精度数据融合方法

本发明属于传感器，尤其涉及一种阵列式mems陀螺仪高精度数据融合方法。

背景技术：

1、微机械陀螺仪(mems陀螺仪)是一种高技术产品，是当代微机械电子系统(mems)领域特别重要的分支之一，它基于微机械加工制造技术生产的，其工作原理是借助科氏力效应，将外部旋转运动转化为陀螺仪内部极板的相对位移。相较于机械陀螺仪及光学陀螺仪，mems陀螺仪包含以下突出特点：(1)体积小，质量轻。mems技术是对微米/纳米材料进行规划、制造、完善、测量与支配的高新技术领域，故mems陀螺仪体积可达到微米/纳米数量级，方便与其他功能芯片进行集成，可直接嵌入到具有主控功能的电路板。(2)高可靠性。由于在制造过程中选取了耐用性高和抗冲击力强的材料，且采取了集成手段，在大多数情况下mems陀螺仪均能正常工作，发挥其功能特性。(3)制造成本低。高精度光学陀螺因制造材料难以获取导致成本高昂，而mems陀螺仪制造使用硅等廉价基础材料，普遍在千元以下，最低数元，在军事设备需求与民用领域等方面都可满足大批量生产，适用性广。

2、mems陀螺仪凭借上述多项显著、独特的优势，在惯性导航、航空航天，汽车及电子设备中得到了广泛的应用。但低成本的mems陀螺仪受到目前在设计与生产过程中无法实现高水平加工制造技术与高要求设计方案的影响，在性能上没有取得比较大的突破，会因其偏置稳定性、非线性和温度稳定性的影响,表现出检测精度低这一普遍缺陷，使其不能满足许多高精度应用的需求。目前提高mems陀螺仪精度的主要方法为以下两种，一是在制造加工mems陀螺时，用一致的信号处理方式对集成多个角速度敏感单元的模块进行处理，但此方法要求有高水平的制造加工工艺和电路设计技术；二是利用mems陀螺仪的优势选用多个精度较低的mems传感器组成阵列，对同一目标进行检测，采集多个传感器数据经过数据融合处理，输出一组高精度与高可信度的数据，实现对运动目标的精密检测，因为最终的输出数据并不来自于单个陀螺仪，而是利用多个陀螺仪的输出融合得到的优化角速度输出信号，因此也称其为“虚拟陀螺技术”。综合考虑这两种方式研发成本和研发时间等因素，构造陀螺阵列来提高mems陀螺仪的精度和可靠性成为目前广泛应用的方式。

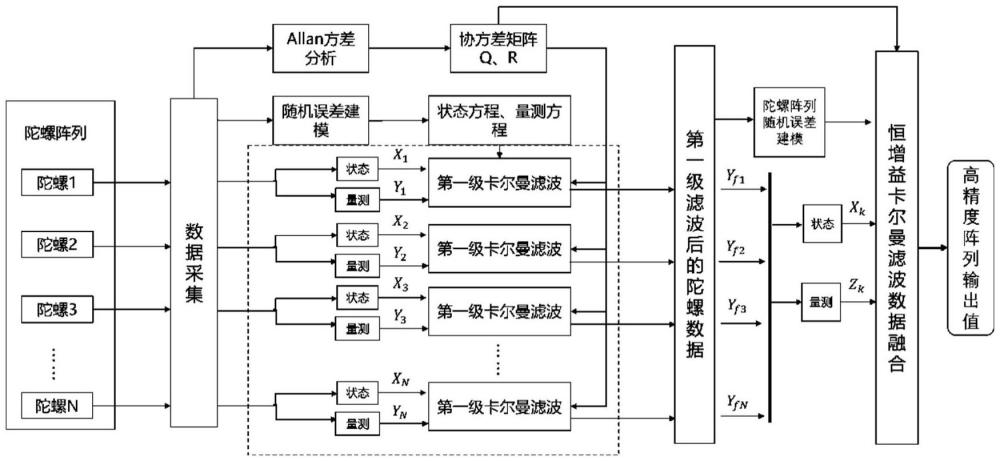
3、多传感器信息融合是阵列式mems陀螺仪研究中的一项关键技术，其是一种对多源数据进行检测，相关，组合和估计从而提高状态估计精度的过程。mems陀螺仪的随机误差是制约其检测精度的主要因素之一。采用多传感器数据融合技术，通过对陀螺阵列的量测值的分析辨识,设计最优滤波器估计出陀螺各项误差的大小,并对量测信息补偿校正,即可得到对输入角速率的高精度估计值。多传感器信息融合过程中，按照对原始数据处理方式不同，主要有两种结构：集中式融合和分布式融合。传统的阵列式mems陀螺仪研究中大多采用基于卡尔曼滤波的集中式融合方法，即将各传感器数据直接送入融合中心通过卡尔曼滤波进行最优估计获取最终高精度估计值。集中式融合的结构简单，信息损失小，但存在对系统通信要求高，融合中心计算负担重等弊端，尤其是阵列中陀螺数量增多时，融合算法的复杂度将显著提升。同时，在卡尔曼递推估计过程中每一步均计算与更新增益与均方差，运算量大，计算复杂，不适合实际应用过程中的实时处理。传统陀螺阵列精度的最终优化效果有限，仍难以满足惯性导航等高精度实际工程应用需求。

技术实现思路

1、本技术实施例的目的是提供一种方法及装置、电子设备，以解决相关技术中存在的单一mesm陀螺随机误差大，检测精度低，难以满足高精度工程应用需求的技术问题。

2、根据本发明的第一方面，提供一种阵列式mems陀螺仪高精度数据融合方法，包括以下步骤：

3、(1)将若干个具有相同型号、敏感轴相互平行测量同一角速度信号的mems陀螺仪构成一陀螺阵列，即阵列陀螺；

4、(2)将阵列陀螺置于水平静止状态下以一定的采样频率连续采样，重复获取多组采样数据，使用采样数据对阵列中各个mems陀螺仪进行allan方差分析，计算各个陀螺仪角度随机游走噪声nai的方差qai及速率随机游走噪声nbi的方差qbi，对多组数据经allan方差分析获取的角度随机游走噪声的方差及速率随机游走噪声的方差求均值，作为最终使用的参数；

5、(3)采用随机游走误差模型对角速度测量值进行随机游走误差建模；并进行第一级卡尔曼滤波设计，即根据建立的随机游走误差模型，采用速率随机游走和真实角速度构建系统状态量，并建立系统状态方程；将各个陀螺仪实际输出值视作量测值,角度随机游走噪声视作量测噪声，构建量测方程；

6、(4)对步骤(3)构建的连续型状态方程和量测方程作离散化处理，得到离散卡尔曼滤波的一步转移矩阵φk,k-1，系统噪声驱动矩阵γk-1，量测序列yk，量测矩阵hk并得到系统噪声离散化协方差矩阵为qk，量测噪声离散化协方差阵rk；利用离散化处理的获得的结果对阵列中各个陀螺进行卡尔曼滤波计算；对状态量xi,k做递推估计，定义速率提取向量e，提取获得各个陀螺的第一级卡尔曼滤波结果；

7、(5)将步骤(3)推导的随机游走误差建模推广至阵列形式；即得到阵列形式的mems陀螺仪随机游走误差模型，并采用陀螺阵列的速率随机游走和真实角速度构建系统状态量，建立状态方程；将经第一级卡尔曼滤波后的阵列中各陀螺数据作为量测值z(t)，陀螺阵列的角度随机游走噪声视作量测噪声，构建量测方程，根据陀螺阵列的状态方程和量测方程进行第二级卡尔曼滤波器设计；

8、(6)对构建的连续型状态方程和量测方程作离散化处理，得到第二级卡尔曼滤波的一步转移矩阵φk,k-1，系统噪声驱动矩阵γk-1，量测序列zk，量测矩阵hk并得到系统噪声离散化协方差矩阵为qk，量测噪声离散化协方差阵rk；

9、(7)推导卡尔曼增益的稳态值以代替每步实时更新的增益值，若状态空间模型为定常系统，则卡尔曼滤波稳定后的滤波增益kk→∞也为定常值；首先定义(n+1)×(n+1)的矩阵随后对l做特征值分解，即l＝adat并使其最后一个特征值为0，和由a,d处理获得；计算连续时间形式的卡尔曼增益稳态值k∞，离散化后计算离散形式的卡尔曼增益稳态值

10、(8)使用步骤(7)推导的离散形式的卡尔曼增益稳态值代替每步更新的增益值，采用恒增益卡尔曼滤波对经第一级滤波后的阵列陀螺进行数据融合，获取高精度角速度估计值；定义矩阵s＝qk1/2a，对状态量xk进行变换，ξ(k)＝s-1xk(k)，利用离散形式的卡尔曼增益稳态值量测序列z(k)对变换后的状态量ξ(k)做递推最小方差估计，为选择向量，为滤波器输出，即陀螺阵列在第k个采样点对输入角速度的最优估计值。

11、进一步地，所述步骤(1)中测量同一角速度信号，具体为：采用将若干个mems陀螺仪分成两两一组，且同组内mems陀螺仪沿敏感轴方向相反安装的形式构建阵列陀螺并进行角速度检测；同组内两个陀螺仪输出端分别接入差分输入a/d转换芯片的正负输入端，经a/d转换得到阵列中每组陀螺的角速度测量值y1(t)，y2(t)，y3(t)，…，yn(t)。

12、具体地，所述步骤(3)中的误差建模是基于对mems陀螺仪信号特征和主要误差源的分析，选择随机游走模型对mems陀螺仪进行误差建模并推广至阵列形式，其中噪声部分包括角度随机游走噪声arw与速率随机游走噪声rrw；对于单个mems陀螺仪的随机游走误差模型为：

13、

14、其中y(t)为mems陀螺输出值，ω(t)为真实角速度，视作由真实角速度白噪声驱动的随机游走噪声,即其中真实角速度驱动白噪声nω的方差为qω；b(t)为陀螺偏差，由白噪声w(t)驱动，对应速率随机游走(rrw)，n(t)为观测噪声，对应角度随机游走(arw)；

15、则阵列形式的随机游走误差模型为：

16、

17、当设y＝[y1,y2,…,yn]t,b＝[b1,b2,…,bn]t、na＝[na1,na2,…,nan]t、nb＝[nb1，nb2,…,nbn]t，则简写为：

18、

19、式中i为陀螺仪序号，n为陀螺仪个数，yi为第i个陀螺仪实际输出角速度，ω为环境真实角速度，bi为第i个陀螺仪偏差，由速率随机游走白噪声nbi驱动，方差为nai为第i个陀螺仪量测噪声，即为角度随机游走白噪声，其方差为

20、进一步地，所述步骤(3)中采用速率随机游走和真实角速度构建系统状态量，具体为：

21、对于阵列中单个陀螺：

22、

23、由此构建的系统的状态方程为：

24、

25、将各个陀螺仪实际输出值视作量测值y(t)＝yi(t)(i＝1,2,…,n),角速随机游走噪声视作量测噪声，则量测方程可构建为：

26、y(t)＝h(t)x(t)+v(t)＝[1 1]·xi(t)+nai；

27、参量w(t)＝[nbi,nω]t,v(t)＝[nai]；按照卡尔曼滤波理论，w(t)、v(t)满足：

28、

29、其中系统噪声协方差矩阵量测噪声协方差矩阵r＝[qai]。

30、进一步地，所述步骤(4)利用离散化处理的获得的结果对阵列中各个陀螺进行卡尔曼滤波计算；对状态量xi,k做递推估计，定义速率提取向量e，提取获得各个陀螺的第一级卡尔曼滤波结果；具体为：利用获得的系统量测序列yk，量测矩阵hk，卡尔曼滤波的一步转移矩阵φk,k-1，系统噪声驱动矩阵γk-1，系统噪声离散化协方差矩阵qk，量测噪声离散化协方差阵rk，按递推计算流程对阵列中各个陀螺进行卡尔曼滤波计算；具体滤波过程为：计算系统一步预测均方误差和系统一步状态预测完成时间更新，进而得到系统滤波增益随后获取新时刻的状态估计和估计均方误差pk＝(i-kkhk)pk/k-1，完成量测更新；将新的状态和均方误差作为下一时刻的计算初值，对xi,k＝[bi,k,ωi,k]t(i＝1,2…n)做递推估计，定义速率提取向量e＝[0，1]，由e.xi,k＝ωi,k即可获得各个陀螺的第一级卡尔曼滤波结果。

31、进一步地，由步骤(5)具体为将随机游走误差建模推广至阵列形式：

32、

33、式中i为陀螺仪序号，n为陀螺仪个数，yi为第i个陀螺仪实际输出角速度，ω为环境真实角速度，bi为第i个陀螺仪偏差，由速率随机游走白噪声nbi驱动，方差为nai为第i个陀螺仪量测噪声，表现为角度随机游走白噪声，方差为

34、设：

35、y＝[y1,y2,…,yn]t,b＝[b1,b2,…,bn]t、na＝[na1,na2,…,nan]t、nb＝[nb1，nb2,…,nbn]t，

36、则上式简写为：

37、

38、进行第二级卡尔曼滤波设计：根据建立的阵列形式随机误差模型，构建系统状态量：

39、

40、由此构建的系统的状态方程为：

41、

42、其中f(t)＝0·in+1，g(t)＝in+1，in为n维单位矩阵；

43、将经第一级卡尔曼滤波后的阵列中各陀螺数据作为量测z(t)＝[yf1(t),yf2(t),…,yfn(t)]t,yfi(t)表示第i个陀螺经第一级滤波后的角速度值；角度随机游走噪声视作量测噪声，量测方程构建为：

44、

45、其中1n表示元素全为1的n维列向量，参量w(t)＝[nb1,nb2,…,nbn,nω]t,v(t)＝[na1,na2,…,nan]t；w(t)、v(t)满足如下表达式：

46、

47、其中系统噪声协方差矩阵量测噪声协方差矩阵r＝[qa]。

48、进一步地，所述步骤(6)具体为：对构建的连续型状态方程和量测方程作离散化处理：

49、

50、式中:

51、

52、t为离散化周期，且wk，vk满足：

53、

54、系统噪声离散化协方差矩阵为量测噪声离散化协方差阵rk＝[qa(k)],qb(k)为速率随机游走噪声矢量nb的协方差矩阵，对角线元素为速率随机游走噪声nbi的方差qω(k)为真实角速度驱动白噪声的协方差矩阵，qa(k)为角度随机游走噪声矢量na的协方差矩阵，对角线元素为步骤二计算的角度随机游走噪声nai的方差

55、进一步地，所述步骤(7)中卡尔曼增益的稳态值计算过程为：首先，定义(n+1)×(n+1)的矩阵随后对l做特征值分解，即l＝adat并使其最后一个特征值为0则和由如下方式从矩阵a,d中推导得到：

56、

57、其中v为最后一列的列向量，为n×n的矩阵，为(n+1)×(n)的矩阵；

58、则连续时间形式的卡尔曼增益稳态值表示为：

59、

60、离散形式的卡尔曼增益的稳态值为：

61、

62、其中ts为离散化周期。

63、进一步地，所述步骤(8)中采用基于离散形式的卡尔曼增益稳态值的恒增益卡尔曼滤波递推估计过程为：定义矩阵s＝q1/2a，对状态量xk进行变换，ξ(k)＝s-1xk(k)，xk＝[b1(k),b2(k),…,bn(k),ω(k)]t，该变换用于隔离纯积分作用，以便采取实际措施确保在实现中不发生数值舍入误差；状态量的估计及融合后的高精度角速度提取由以下方程完成：

64、

65、其中为ξ(k)的最小方差估计，的最后一行设置为0，其对应于纯积分器状态；为选择向量，为滤波器输出，即陀螺阵列在第k个采样点对输入角速度的最优估计值。

66、本发明的第二方面：一种电子设备，包括：

67、一组或多组mems陀螺阵列

68、一个或多个处理器用于读取mems陀螺阵列数据并进行处理；

69、存储器，用于存储一个或多个程序；

70、当所述一个或多个程序被所述一个或多个处理器执行，使得所述一个或多个处理器实现所述的阵列式mems陀螺仪高精度数据融合方法。

71、本发明包括以下有益效果：降低了mems陀螺仪随机误差并显著提高mems陀螺仪检测精度；利用卡尔曼增益的稳态值进行角速度的估计，避免了每步对增益和均方差的计算，优化处理过程的复杂度和运算量，更利于陀螺阵列的实时处理。本发明通过构建陀螺阵列并进行数据融合，在多传感器数据进入融合中心前，采用卡尔曼滤波对各个传感器进行局部最优估计，获取单个陀螺的第一级估计值，再将处理后的信息送入第二级融合中心进行处理，获取最终的高精度估计值以降低mems随机误差并显著提高检测精度。

72、应当理解的是，以上的一般描述和后文的细节描述仅是示例性和解释性的，并不能限制本技术。