一种面向长尾分布的模糊多标记分类方法
本发明涉及机器学习和数据挖掘领域,具体涉及一种基于模糊规则的长尾多标记分类方法。
背景技术:
0、技术背景
1、标记的稀疏性通常使多标记数据集服从长尾分布。即按照标记出现的频率降序排列,得到的频率分布是长尾的,其中大量的标记只与极少的样本相关(又叫尾标记),而只有少量的标记与大量的样本相关(又叫头标记)。在许多实际应用场景中,长尾分布问题尤为突出。例如:在车联网中,交通状况、事故类型和道路条件的标记往往具有长尾分布特性。大多数情况下,常见的交通状况和事故类型样本较多(头标记),而罕见的交通状态和特殊事故类型样本稀少(尾标记)。在生物信息学中,某些罕见疾病或基因突变也是长尾分布的典型案例。在情绪感知领域,一些细微或不常见的情绪状态也存在类似问题。
2、与头标记相比,尾标记的相关样本不充分,造成传统模型对尾标记的决策偏差较大。目前,能处理多标记场景下长尾分布问题的方法大体上可归纳为三个方向:即,合适的采样策略,知识迁移,以及构建复杂的(合成的)目标函数。对于合适的采样策略,目前这个方向的解决思路需要借助传统的基于单标记的采样策略。例如将长尾多标记分类任务拆分成多个不平衡二元分类任务。在每个二元分类任务中,该方法对不相关样本进行多次欠采样学习,并产生多个决策边界,再利用融合策略将多个策略边界整合为一个综合边界。对于知识迁移,这个方向目前可归纳为两种思路:一种是实现标记内迁移。即,多标记长尾分布问题被拆成多个独立的单标记类别不平衡问题,实现大类到小类的知识迁移。另一种是实现标记间迁移。这个思路是专门针对多标记长尾分布问题而设计的,并采用知识迁移将头标记的知识迁移到尾标记。对于构建复杂的(合成的)目标函数,这个方向直接针对多标记长尾分布问题构建适合的目标函数。
3、上述三个方向都可以解决多标记场景下的长尾分布问题,但几乎没有方法能同时关注如下三个问题:1)如何丰富尾标记的可学习知识。2)如何减小尾标记的决策偏差。3)如何利用标记之间的关系来提升预测性能。因此,亟待发展出有效的长尾多标记学习方法来兼顾上述三个挑战。
技术实现思路
1、本发明的目的是提供一种适用于多种领域的基于模糊规则的长尾多标记分类方法,旨在解决不同领域的多标记数据集中尾标记稀缺导致的可学习知识贫瘠、决策偏差较大和标记关系未充分利用的问题。通过引入模糊规则和相关学习机制,本发明能够有效挖掘数据中的潜在信息、减少因长尾分布引起的决策偏差、并利用标记之间的共现关系提升预测性能。该方法在生物信息学、情绪感知等实际应用场景中具有广泛的应用前景。
2、本发明的技术方案如下:
3、一种面向长尾分布的模糊多标记分类方法,步骤如下:
4、训练阶段步骤为:
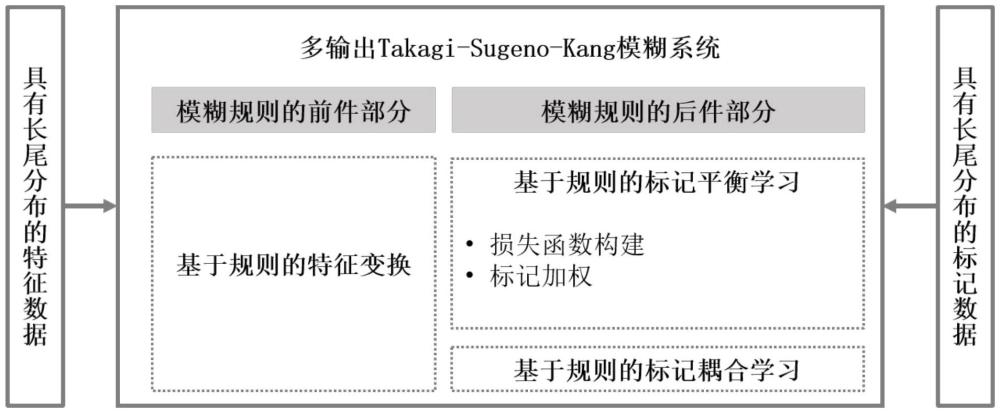
5、第一步:基于模糊规则的特征变换。具体过程如下:
6、对于含有k条推理规则的多输出takagi-sugeno-kang模糊系统,它的第k条推理规则可表示如下:
7、
8、其中xj(1≤j≤d)代表实例x的第j个特征,d表示特征维度,表示实例x的第j个特征在第k条规则上的前件模糊集,是第j个特征在第k条规则上对应于第l个输出的后件参数,是实例x在第k条规则上的第l个输出。
9、公式(1)中的前件模糊集可通过高斯隶属度函数来描述,即:
10、
11、其中和可通过fuzzy c-means(fcm)聚类方法获得:
12、
13、其中uik表示第i个实例在第k条推理规则上的隶属值,可通过fcm计算获得。
14、∈是超参数,用于调整
15、根据上述分析,实例x在第k条规则上的点火水平可表示为:
16、
17、其中公式(6)是公式(5)的标准化形式。最后,实例x在多输出tsk fs中的第l个输出被表达为:
18、
19、进一步地,公式(7)可以被重新表达为实例x在模糊特征空间的线性模型:
20、
21、其中,
22、
23、那么,对于多标记数据中的第i个实例xi(1≤i≤n),在模糊规则数被设置为k的前提下,它在模糊特征空间对应的模糊特征向量是具体映射过程可参考公式(2)-(6)以及(9)-(11)。也就是说,
24、φ1(xi)=xg,i (12)
25、相应地,对于多标记数据集的输入矩阵x=[x1,x2,…,xn],它经过φ1可得到如下模糊特征矩阵:
26、
27、与原始特征相比,高维模糊特征空间下的模糊特征具有一个内在的优势。即,模糊特征对实例的表达能力更强。这意味着尾标记可以从模糊特征中学习到更丰富的隐含知识。
28、第二步:基于模糊规则的标记平衡学习。具体过程如下:
29、对于第j个标记向量(即y中的第j行元素),它在多输出takagi-sugeno-kang模糊系统中对应的输出被线性表达为:
30、
31、其中对应第j个标记在多输出takagi-sugeno-kang模糊系统中的后件参数向量。那么,cj的最优解可通过最小二乘法求得,即:
32、
33、公式(15)即为特征与第j个标记之间线性回归的损失函数。
34、为公式(15)中第j个标记的学习过程进行加权是平衡尾标记决策偏差的关键。本发明采用一种温和且灵活的方式进行加权。即,在不进行人工分离头标记与尾标记的情况下获得第j个标记的学习权重qj(1≤j≤l)。具体地,
35、
36、其中,
37、pj=oj/m (17)
38、oj=|{n|ynj=1,1≤n≤n}| (18)
39、
40、其中oj代表第j个标记出现的频率(即相关样本量),公式(16)-(19)表明第j个标记出现的频率越小,对应的权重qj(qj>0)越大。因此,公式(15)可以被改进为:
41、
42、与公式(15)相比,公式(20)更适合服从长尾分布的多标记学习场景。主要原因是qj的引入使本发明能够在一定程度上缓解尾标记因相关样本量少而得不到充分学习的问题,这有利于降低尾标记的决策偏差。
43、综合上述分析,基于模糊规则的标记平衡学习即可被表达为:
44、
45、
46、其中并且进一步地,我们为公式(21)加入正则化项,即,
47、
48、其中β>0是一个超参数,用于平衡基于模糊规则的标记平衡学习和模型复杂度的影响。
49、第三步:基于模糊规则的标记耦合学习。具体过程如下:
50、首先,本发明采用皮尔逊相关系数来度量标记空间中和之间的共现关系,并记为uij。一般地,-1≤uij≤1。当标记向量和之间是正相关时,uij>0,否则,uij<0。标记向量和之间的相关性越强,uij的绝对值越大。
51、其次,在多输出takagi-sugeno-kang模糊系统中,模糊后件向量ci和cj能够为和筛选判别特征。这意味着ci和cj之间的相互关系应该与标记向量和之间的耦合关系是一致的。
52、结合上述分析,基于模糊规则的标记耦合学习可进一步优化多输出takagi-sugeno-kang模糊系统的后件参数,具体公式被定义为:
53、
54、其中且aij=1-uij。
55、第四步:通过整合上述三个步骤,实现完整的基于模糊规则的长尾多标记学习目标函数。在多种标记呈现长尾分布特点的应用场景下,仍能有效预测多种标记结果。
56、使用阶段步骤为:
57、第五步:利用多输出takagi-sugeno-kang模糊系统的前件部分将具有长尾分布特点的多标记测试数据转换为模糊特征数据。
58、第六步:将模糊特征数据与优化后的多输出takagi-sugeno-kang模糊系统后件参数做线性回归,并基于阈值函数实现应用场景中的长尾多标记预测。
59、本发明的优点包括以下几点:
60、1)通过基于模糊规则的特征变换,本发明利用模糊规则的前件部分将原始特征映射到模糊特征空间,为尾标记的学习挖掘了丰富的潜在知识。
61、2)通过基于模糊规则的标记平衡学习,本发明在利用模糊规则的后件部分为模糊特征空间与标记空间构建映射关系(即损失函数)时,引入了自适应加权,从而缓解了尾标记决策偏差较大的问题。
62、3)通过基于模糊规则的标记耦合学习,本发明为标记空间中的任意两个标记建立耦合来分析它们的共现关系,从而利用标记共现关系来进一步提高长尾多标记学习的预测性能。
63、4)大量的实验分析证明本发明在多种领域处理长尾多标记学习问题上的有效性。
- 还没有人留言评论。精彩留言会获得点赞!