一种河流视频水位-流速-流量三维曲面计算方法与装置

本技术涉及水文测验领域，尤其是涉及一种河流视频水位-流速-流量三维曲面计算方法与装置。

背景技术：

1、流量是水文测验中最基本和最重要的观测要素之一，可以作为水文预报、水动力仿真、水资源管理的数据支撑，为防汛抗旱、水库调度以及水资源计划与调配提供决策依据。目前用于河道流量测验的基本方法为流速面积法，其原理为沿断面方向均匀设置若干条测速垂线将河道断面划分为若干个子区域，利用测速仪器测量各测速垂线平均流速，根据测得水位和河床底部高程计算各垂线处水深以及子区域面积，垂线平均流速与子区域面积的乘积即为子区域的流量，各子区域流量累加即为断面流量。传统接触式测流方式利用流速仪测量测速垂线不同深度的流速来计算垂线平均流速，要完成整个断面的流速测量历时较长，难以捕捉流量的瞬时变化，且依赖人工操作，在暴雨山洪等条件下难以施测，无法实现全天候无间断的连续流量测验。流速面积法需要频繁测量断面的水深和流速，并计算多个子断面流量进行求和，计算流程相对复杂，测量过程中的误差来源较多，包括：水位、点流速的测量误差，垂线平均流速的计算，垂线数目的设置等，对于测验结果的不确定性进行量化比较困难。

2、相比于流量监测，连续的水位监测实施难度较小。因此在水文资料整编时，通常会根据实测的多组水位、流量值建立水位流量关系，然后根据水位资料和水位流量关系计算连续的流量序列。由于下游边界条件变化造成的回水，洪水涨落过程等因素的影响，在断面控制条件相对稳定的情况下，水流会出现比降的变化。因此水位流量关系通常会表现为绳套曲线，利用单一的水位流量关系推求流量会出现较大的不确定性。

3、随着视频、雷达等非接触式测流技术的发展，可以实现与水位监测同步的表面流速监测。由于水位和表面流速都可以作为河道水流状态以及流量变化的直观表现，在符合物理意义和数学原理的前提下构建一种根据视频水位和表面流速计算流量的函数关系，并对拟合结果的不确定性进行量化，可以有效简化利用流速面积法测量流量的计算流程，相比于单一水位流量关系更能反映水流的状态变化，具备较强的应用价值和实践意义。

技术实现思路

1、针对现有技术的不足之处，本技术提供一种河流视频水位-流速-流量三维曲面计算方法与装置，融合流量计算原理、信息熵理论以及断面几何特征得到简化的流量计算模型，在河道水位流量关系模型的基础上引入表面流速反映水流运动状态的变化，进而利用变分贝叶斯推断优选模型参数分布，数学机理和物理意义明确，计算过程简洁，误差来源清晰，能够适应不同断面情况。

2、本技术提供的一种河流视频水位-流速-流量三维曲面计算方法采用如下的技术方案：

3、一种河流视频水位-流速-流量三维曲面计算方法，包括以下步骤：

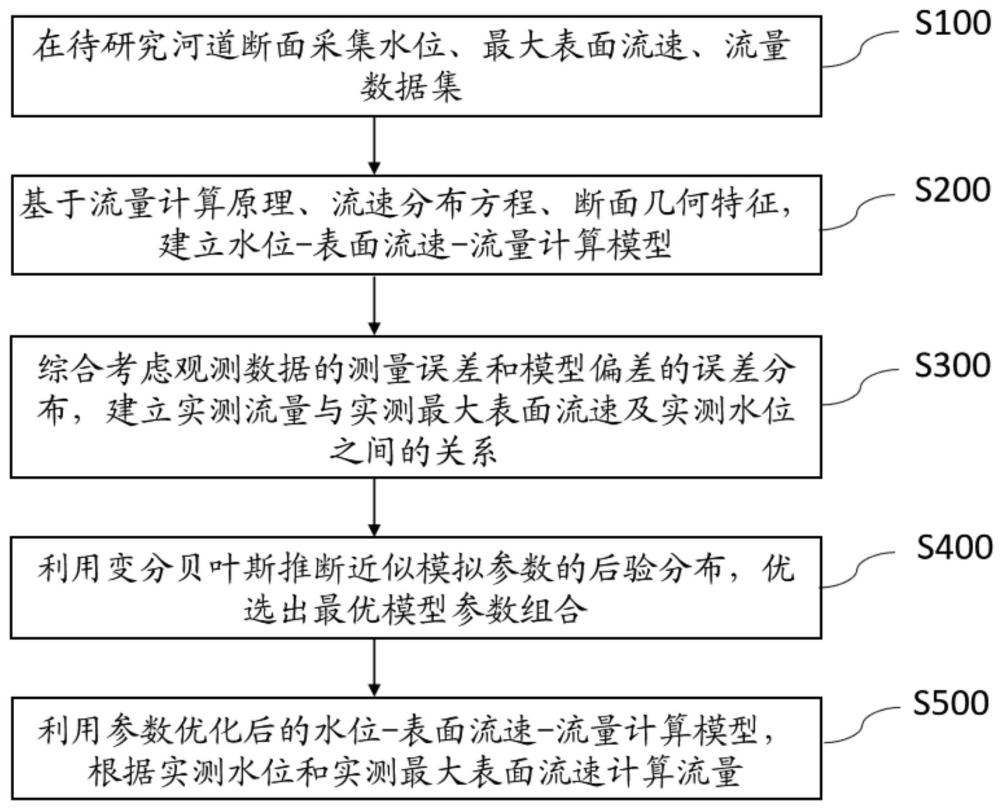
4、采集水文测验数据：在待研究河道断面采集数据集s，s={}；其中，是水位测量值，是最大表面流速测量值，是流量测量值；

5、构建水位-最大表面流速-流量计算模型：将河道断面的流量表示为断面平均流速与断面面积的乘积，建立断面平均流速与最大表面流速之间的关系，以及断面面积与水位之间的关系；将断面平均流速由最大表面流速表示，断面面积由水位表示，得到水位-最大表面流速-流量关系模型的一般表达形式：

6、

7、其中， q为流量， v为最大表面流速， h为水位， a、 b、 c均为模型参数；

8、综合考虑观测数据的测量误差和模型偏差的误差分布，建立实测流量与实测最大表面流速及实测水位之间的关系；

9、利用变分贝叶斯推断近似模拟参数的后验分布，优选出最优模型参数组合，得到参数优化后的水位-最大表面流速-流量计算模型；

10、计算流量：利用参数优化后的水位-最大表面流速-流量计算模型，根据实测水位和实测最大表面流速计算流量。

11、进一步地，采集水文测验数据步骤中，水位和最大表面流速的采集手段为非接触式测量手段，包括图像测量手段，水位和最大表面流速的测量手段在模型建立阶段和模型应用阶段保持一致；流量的测量方式包括流速仪和adcp仪器。

12、进一步地，构建水位-最大表面流速-流量计算模型步骤中，建立断面平均流速与最大表面流速之间关系的方法包括：

13、以断面最大流速和最大表面流速所在的铅垂线作为y轴，断面横向方向作为z轴，建立y轴上流速与深度的关系以及流速的累积分布函数；

14、建立断面最大流速与表面流速之间的关系；

15、基于以信息熵理论为基础的速度分布方程，将断面最大流速转化为断面平均流速；

16、基于断面最大流速与表面流速之间的关系，以及断面最大流速与断面平均流速之间的关系，得到断面平均流速与最大表面流速的关系。

17、进一步地，构建水位-最大表面流速-流量计算模型步骤中，根据断面几何特征构建断面面积与水位的关系，分别分析河道断面形状为矩形、梯形、抛物线形的情况，结合断面平均流速与最大表面流速的关系，得到流量与水位、最大表面流速的关系为。

18、进一步地，综合考虑观测数据的测量误差和模型偏差的误差分布，得到实测流量关于实测最大表面流速和实测水位的表达形式的方法包括：

19、水位、最大表面流速、流量的观测值是对真实值的估计，观测值与真实值之间满足以下关系：

20、

21、其中，分别为水位、最大表面流速、流量的观测值，分别为水位、最大表面流速、流量的真实值，下标 i为观测数据的编号；为最大表面流速观测值的误差分布，满足均值为0、标准差为 uv的正态分布；为流量观测值的误差分布，满足均值为0、标准差为 uq的正态分布；n（）表示正态分布；

22、将水位-最大表面流速-流量关系模型写作的形式，考虑模型偏差：

23、

24、其中， θ为模型参数， εif为模型模拟的误差分布，满足均值为0、标准差为 σf的正态分布；

25、假定各误差分量间相互独立，得到实测流量关于实测最大表面流速和实测水位的表达形式：

26、。

27、进一步地，利用变分贝叶斯推断近似模拟参数的后验分布的方法包括：

28、以最小化kl散度为目标，在概率空间寻找与参数的后验分布接近的概率分布：

29、

30、arg min kl（）表示最小化kl散度时自变量的取值；

31、将最小化kl散度等价为最大化的elbo函数：

32、

33、其中，代表似然函数，代表参数的先验分布，e[ ]为数学期望；

34、似然函数表示为以下的形式：

35、

36、其中， n为观测数据的总数， i为观测数据的编号；表示服从期望为 m，标准差为 s的正态分布的概率密度函数在 x处的取值，表示服从期望为、标准差为的正态分布的概率密度函数在处的取值；

37、假设待求参数间相互独立，先验分布的概率密度函数表示为：

38、

39、其中， n为参数的总数， i为参数的编号， θn为第n个参数的概率密度函数， p( σf)、 p( a)、 p( b)、 p( c)分别为参数 σf、 a、 b、 c的概率密度函数。

40、进一步地，利用变分推断近似模拟参数的后验分布，优选出最优模型参数组合的步骤还包括：通过随机梯度上升算法优化求解概率分布近似参数的后验分布。

41、进一步地，所述随机梯度上升算法包括以下步骤：

42、步骤1、令的初始分布为多元正态分布；

43、步骤2、假设的待求参数为 φ，求该轮次elbo函数的梯度：

44、

45、其中，为梯度算符，式中的期望e通过蒙特卡洛采样来近似，得到该迭代轮次的梯度；

46、步骤3、得到梯度后，沿着使elbo函数值上升的方向更新参数 φ；

47、步骤4、重复步骤2和3，直至梯度收敛，得到优化的参数 φ。

48、本技术还提供一种河流视频水位-流速-流量三维曲面计算装置，用于实施一种河流视频水位-流速-流量三维曲面计算方法，装置包括：

49、数据采集模块：用以采集构建水位-流速-流量分布关系所需的同一时刻对应的水位、最大表面流速和流量数据；

50、模型构建模块：用以根据采集的水位、最大表面流速和流量数据利用变分贝叶斯推断优选参数构建流量计算公式；

51、流量计算模块：用以根据水位和最大表面流速计算断面流量及置信区间。

52、本技术还提供一种计算机程序产品，包括计算机程序，所述计算机程序被处理器执行时实现一种河流视频水位-流速-流量三维曲面计算方法。

53、综上所述，本技术包括以下至少一种有益技术效果：

54、1.本技术能够根据水位和最大表面流速快速计算出流量，实现流量的远程实时监测，相比于传统的流速面积法，函数形式和计算流程均有所简化；

55、2.传统的水位流量关系仅考虑单一曲线关系，本技术在水位流量关系的基础上引入最大表面流速，能够准确反映流量规律，适应不同断面情况；

56、3.在不确定性分析方面，传统的流速面积法在流量测量时误差来源较多，不确定性传递过程复杂，不确定性分析难度较大；传统的水位流量关系曲线仅考虑模型拟合偏差，且参数往往是固定值，不确定性来源不准确；本技术综合考虑测量误差和模型拟合偏差，不确定性来源清晰，根据贝叶斯原理得到模型参数的概率分布，便于进行结果的不确定性计算。