基于飞轮驱动的可维修卫星惯性参数在轨辨识方法

本发明涉及航天领域的在轨服务，尤其涉及一种基于飞轮驱动的可维修卫星惯性参数在轨辨识方法、装置、设备及计算机可读存储介质。

背景技术：

1、在轨服务技术能够对可维修卫星执行在轨模块替换与升级等操作，具有良好的应用前景，受到了国内外学界与工业界的广泛关注。但是，由于在轨装配误差的影响，发生模块更换后的卫星质心将会发生一定的偏移，继而影响卫星姿态动力学特性。如若仍然按照原有姿态稳定律进行控制，将导致控制性能的下降。

2、可维修卫星往往具有较高的研发水平和应用价值，其主要能够执行观测等高价值空间任务，因此其对姿态指向性有着极高的需求。姿态指向能力的下降将导致任务性能的下降，甚至可能导致任务失败。因此有必要研究面向可维修卫星的惯性参数辨识方法，提升卫星的动力学模型精度，继而保障观测与通讯等任务的有效进行。

3、针对卫星惯性参数辨识，现有研究的方法主要是将卫星的姿态动力学模型改写成与辨识参数线性相关的形式，然后利用卫星自身搭载的反作用发动机产生推力，将测量到的卫星运动状态参数输入到辨识方程中进行求解。这些方法主要存在以下几个不足之处：

4、1)辨识过程将消耗卫星宝贵的燃料资源，卫星的在轨寿命将受到影响，降低效费比；

5、2)未充分考虑测量噪声的影响，没有用到相应的统计学信息，辨识精度受测量噪声影响明显；

6、3)需要完整的状态测量量，在部分传感器发生等情况时，无法求解，限制了应用范围。

技术实现思路

1、本技术实施例通过提供一种基于飞轮驱动的可维修卫星惯性参数在轨辨识方法，旨在克服现有技术存在的上述局限。

2、为实现上述目的，本技术实施例提供了一种基于飞轮驱动的可维修卫星惯性参数在轨辨识方法，包括以下步骤：

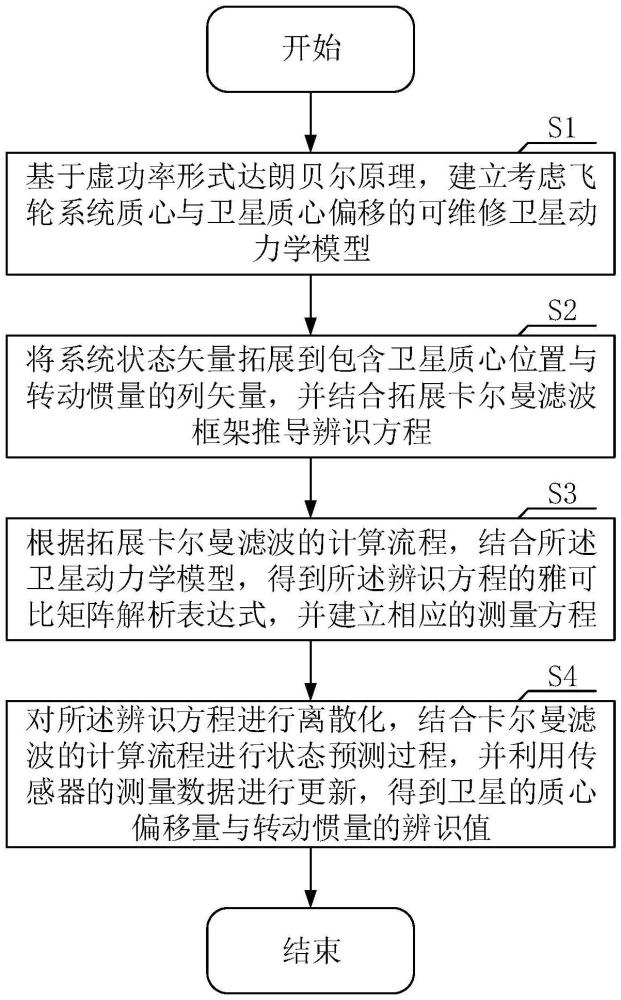
3、s1、基于虚功率形式达朗贝尔原理，建立考虑飞轮系统质心与卫星质心偏移的可维修卫星动力学模型；

4、s2、将系统状态矢量拓展到包含卫星质心位置与转动惯量的列矢量，并结合拓展卡尔曼滤波框架推导辨识方程；

5、s3、根据拓展卡尔曼滤波的计算流程，结合所述卫星动力学模型，得到所述辨识方程的雅可比矩阵解析表达式，并建立相应的测量方程，所述测量方程的测量量包括飞轮的角速度和卫星的运动状态；

6、s4、对所述辨识方程进行离散化，结合卡尔曼滤波的计算流程进行状态预测过程，并利用传感器的测量数据进行更新，得到卫星的质心偏移量与转动惯量的辨识值。

7、在一实施例中，步骤s1包括：

8、假设卫星参考质心与惯性系参考点之间通过虚铰相连，所述虚铰包括3个转动自由度和3个平动自由度；

9、利用虚功率形式的达朗贝尔原理，建立卫星动力学模型，所述卫星动力学模型表达式如下：

10、

11、其中，q、分别表示广义坐标及其一阶与二阶导数，θ表示需辨识的惯性参数，z(q,θ)表示广义质量矩阵，表示广义力矢量，u表示铰上的控制力矩；

12、其中，z(q,θ)和的表达式如下：

13、z(q,θ)＝αtmα+βtjβ；

14、

15、其中，α和β与卫星与各个飞轮之间的相对位置矢量和飞轮转轴方向相关，m和j皆为对角矩阵，其中m对角元为卫星和各个飞轮的质量，j对角元为卫星和飞轮在惯性系下的转动惯量，fo为卫星和飞轮所受外力组成的列向量，mo为卫星和飞轮所受外力矩组成的列向量，w表示各个物体的惯性力，σ和ε表示惯性力矩，fτq表示约束力元。

16、在一实施例中，步骤s2包括：

17、s21、基于拓展系统状态矢量得到所述列矢量得到卫星动力学模型的矩阵形式：

18、

19、其中，将卫星的广义坐标q分为q1和qw两部分，其中，q1表示卫星本体的运动参数，qw表示飞轮的转动角；

20、s22、针对飞轮驱动场景，其角加速度已知，即的理论值已知，利用整逆混合动力学模型，得到辨识方程如下：

21、

22、在一实施例中，步骤s3包括：

23、s31、利用链式求导法则，对广义质量矩阵z和广义力矢量z相对系统广义坐标进行微分，得到如下表达式：

24、

25、s32、计算和来得到上式的解析表达式：

26、对方向余弦阵aj求对ql的偏导数，可以得到：

27、

28、其中，由第j个关节铰确定，因此可以通过递推技术计算得到

29、对于和可以写成：

30、

31、因此，

32、

33、由于和由j号关节铰及其坐标qj决定，因此，和可以在得到之后通过递推的方法计算得到；

34、当得到和后，和可以通过链式求导法则计算得到，然后可计算得到和

35、对于其影响ω、σ和ε，因此

36、为计算将角速度对ql求导，可以得到：

37、

38、其中，可以通过递推方法得到；

39、对于和可以通过计算直接得到；

40、当计算得到和后，可以通过链式求导法则得到；

41、对于目标转动惯量j'1，将j替换成代入到卫星动力学模型中，得到相应的导数项；

42、对于基座质心到参考点在本体系下的位置矢量b1，将b1'替换成[1,0,0]t、[0,1,0]t或者[0,0,1]t及其它b'n替换成[-1,0,0]t、[0,-1,0]t与[0,0,-1]t来计算和其中，i＝x,y,orz；

43、采用链式求导法则，得到和的雅可比矩阵解析表达式，继而可以得到所述辨识方程对状态矢量x的解析表达式；

44、s33、建立测量方程：

45、假设测量方程的测量量包括飞轮的角速度和卫星的运动状态，为了分析测量量类型对辨识性能的影响，将卫星的运动状态分为包括参考质心矢量及参考质心姿态角的第一状态，和包括参考质心矢量、参考质心速度、参考质心姿态角及参考质心角速度的第二状态，建立测量方程的通式，如下：

46、y(tk)＝hx(tk)+μ；

47、其中，tk＝kt，t表示测量周期，h为一个常值矩阵，μ表示测量噪声。

48、在一实施例中，在步骤s4中，所述辨识方程的离散化形式如下：

49、xk＝f(tk-1,xk-1,ωk)。

50、在一实施例中，在步骤s4中，卡尔曼滤波的预测过程如下：

51、xk|k-1＝f(tk-1,xk-1,0)；

52、

53、其中，

54、

55、更新过程如下：

56、

57、xk|k＝xk|k-1+kk[yk-h(xk|k-1)]；

58、pk|k＝pk|k-1-kkhkpk|k-1。

59、为实现上述目的，本技术实施例还提出一种基于飞轮驱动的可维修卫星惯性参数在轨辨识装置，包括：

60、动力学模型建立模块，用以基于虚功率形式达朗贝尔原理，建立考虑飞轮系统质心与卫星质心偏移的可维修卫星动力学模型；

61、推导模块，用以将系统状态矢量拓展到包含卫星质心位置与转动惯量的列矢量，并结合拓展卡尔曼滤波框架推导辨识方程；

62、测量方程建立模块，用以根据拓展卡尔曼滤波的计算流程，结合所述卫星动力学模型，得到所述辨识方程的雅可比矩阵解析表达式，并建立相应的测量方程，所述测量方程的测量量包括飞轮的角速度和卫星的运动状态；

63、预测与更新模块，用以对所述辨识方程进行离散化，结合卡尔曼滤波的计算流程进行状态预测过程，并利用传感器的测量数据进行更新，得到卫星的质心偏移量与转动惯量的辨识值。

64、为实现上述目的，本技术实施例还提出一种基于飞轮驱动的可维修卫星惯性参数在轨辨识设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的基于飞轮驱动的可维修卫星惯性参数在轨辨识程序，所述处理器执行所述基于飞轮驱动的可维修卫星惯性参数在轨辨识程序时实现如上述任一项所述的基于飞轮驱动的可维修卫星惯性参数在轨辨识方法。

65、为实现上述目的，本技术实施例还提出一种计算机可读存储介质，所述计算机可读存储介质上存储有基于飞轮驱动的可维修卫星惯性参数在轨辨识程序，所述基于飞轮驱动的可维修卫星惯性参数在轨辨识程序被处理器执行时实现如上述任一项所述的基于飞轮驱动的可维修卫星惯性参数在轨辨识方法。

66、与现有技术相比，本技术具有以下有益的技术效果：

67、现有卫星惯性参数的辨识方法往往需要消耗卫星的燃料，这将影响其使用寿命，且未充分考虑测量噪声的影响，抗噪声能力较差。针对发生模块更换后，可维修卫星的惯性参数辨识问题，本技术在建立考虑飞轮系统质心与卫星质心偏移的动力学模型基础上，结合拓展卡尔曼滤波方法，能够在仅飞轮驱动的情况下辨识出卫星质心的偏移量与转动惯量，且方法具有较高的鲁棒性、适应性和抗干扰能力。