一种平头弹撞击下正交层压板背凸变形及弹道极限速度确定方法

本发明涉及一种平头弹撞击下正交层压板背凸变形及弹道极限速度确定方法，属于毁伤和防护。

背景技术：

1、超高分子量聚乙烯(uhmwpe)纤维复合材料因其卓越的力学性能，如高比强度和比模量，以及极高的塑性波速，能够快速吸收和分散能量，越来越多地应用于装甲防护系统中。典型的交叉铺层uhmwpe层压板由高体积分数的uhmwpe纤维复合材料(>80％)与低体积分数的热塑性聚合物基体(<20％)构成，具有优异的抗高速局部冲击性能。

2、uhmwpe正交层压板的动态失效过程包括局部侵彻阶段和伴随渐进侵彻的背凸变形阶段，背凸变形和弹道极限速度是评估其防弹性能的重要指标。现有的数值模型虽然能提供高保真的弹道响应预测，但计算成本高，难以用于大规模的迭代仿真优化。因此，开发一种能够快速且准确地估算背凸变形和弹道极限速度的解析模型非常重要。

3、在弹道冲击过程中，层压板的背凸变形与由从中心向外传播的移动铰密切相关。现有的基于动量守恒或能量守恒的解析模型往往忽略了层压板的渐进侵彻过程，多利用经验公式来计算横向变形的演变，且经验公式多需要结合实验或仿真来结合相关的参数，从而导致而背凸变形和弹道极限速度预测的复杂度较高而准确性不足。

技术实现思路

1、有鉴于此，本发明提供了一种平头弹撞击下正交层压板背凸变形及弹道极限速度确定方法，能够高效准确的预测uhmwpe层压板在平头弹撞击下的瞬态中心挠度、移动铰位置及弹道极限速度。本发明中所涉及的术语“移动铰”，是指沿层压板面内方向弯曲波随时间的传播，也即层压板横向变形轮廓。

2、本发明能够准确预测uhmwpe层压板在平头弹渐进侵彻过程中的瞬态背凸变形、移动铰传播和弹道极限速度，而不需要使用任何拟合参数和经验公式。

3、本发明的技术解决方案是：

4、一种平头弹撞击下正交层压板背凸变形及弹道极限速度确定方法，该方法的步骤包括：

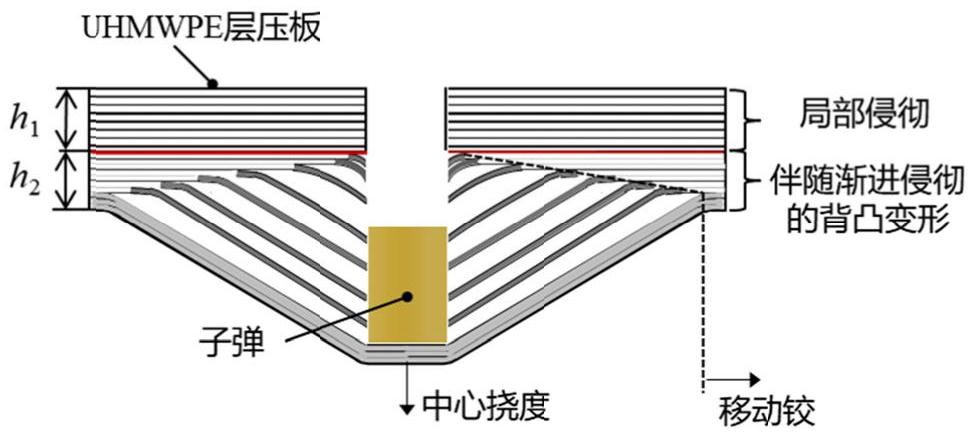
5、第一步，使用初始速度为v01的平头弹正撞击固支正交层压板1，平头弹的撞击位置为正交层压板的中心，此时正交层压板被侵彻，正交层压板被侵彻过程分为局部侵彻阶段和伴随渐进侵彻的背凸变形阶段；

6、使用初始速度为v02的平头弹正撞击固支正交层压板2，平头弹的撞击位置为正交层压板的中心，此时正交层压板被侵彻，正交层压板被侵彻过程分为局部侵彻阶段和伴随渐进侵彻的背凸变形阶段；

7、…

8、使用初始速度为v0n的平头弹正撞击固支正交层压板n，平头弹的撞击位置为正交层压板的中心，此时正交层压板被侵彻，正交层压板被侵彻过程分为局部侵彻阶段和伴随渐进侵彻的背凸变形阶段；

9、第二步，根据第一步平头弹的初始速度v01，获得平头弹撞击下正交层压板背凸变形参数c1和平头弹的剩余速度为vr1；

10、根据第一步平头弹的初始速度v02，获得平头弹撞击下正交层压板背凸变形参数c2和平头弹的剩余速度为vr2；

11、…

12、根据第一步平头弹的初始速度v0n，获得平头弹撞击下正交层压板背凸变形参数cn和平头弹的剩余速度为vrn；

13、第三步，对第二步得到的v01、vr1、v02、vr2、…、v0n、vrn进行拟合，得到弹道极限速度vbl。

14、所述第一步中，平头弹与正交层压板的材料参数包括平头弹质量mp，正交层压板的密度ρ，正交层压板纤维x方向弹性模量e1和y方向弹性模量e2，正交层压板厚度方向弹性模量e3，面内方向泊松比v12，面内方向剪切模量为g12，失效应力σf，失效应变∈f；

15、平头弹与正交层压板几何参数包括子弹的横截面积a，正交层压板边长a、b及正交层压板厚度h0；

16、所述第二步中，正交层压板背凸变形参数包括中心挠度w0、x方向的移动铰位置ζ和y方向的移动铰位置η；x方向与正交层压板的0°纤维方向重合，y方向与正交层压板的90°纤维方向重合，z方向为正交层压板的厚度方向；平头弹撞击下正交层压板背凸变形参数通过数值求解下列微分方程组计算得到：

17、

18、其中，l为拉格朗日值，与伴随渐进侵彻的背凸变形阶段的正交层压板的厚度h相关；

19、的为伴随渐进侵彻的背凸变形阶段的平头弹速度，其初值为局部侵彻阶段的平头弹剩余速度vm，其终值为平头弹的剩余速度vr；

20、基于里兹法及边界条件假定层压板位移场的试函数，并根据正交层压板的应变能∏和系统总动能t(层压板的动能及子弹的动能)，计算拉格朗日值l；

21、伴随渐进侵彻的背凸变形阶段的正交层压板厚度h，其初值为h2＝h0-h1，h0为正交层压板的初始总厚度，h1为局部侵彻阶段的侵彻厚度；

22、在计算伴随渐进侵彻的背凸变形阶段的正交层压板厚度时对剩余未穿透正交层压板进行均质化分层建模，且依据混合模式失效判据和拉伸失效判据预测正交层压板的渐进侵彻过程，与平头弹接触的均质层在满足失效判据后即发生穿透，其中心点挠度和移动铰位置不再增大；

23、局部侵彻阶段平头弹速度表达式为：

24、

25、式中：v0为子弹初始速度，具体取值为v01、v02、...、v0n；t为响应时间；ch为层压板中压缩波传播速度，

26、由式(1)积分可得局部侵彻阶段的侵彻深度：

27、

28、式中：t1为局部侵彻阶段的终止时间；

29、局部侵彻阶段的终止时间为：

30、

31、联立式(2)和(3)，可求得平头弹的局部侵彻阶段的侵彻厚度h1及平头弹的剩余速度

32、将伴随渐进侵彻的背凸变形阶段的正交层压板建模为n个均质层，每个均质层由[0/90]组成，厚度为hl，则均质层的材料力学性能参数与层压板的宏观力学性能参数相同；

33、伴随渐进侵彻的背凸变形阶段的正交层压板位移场试函数表达式为：

34、

35、式中：w0(t)为正交层压板中心点挠度，ζ(t)和η(t)分别为x，y方向的移动铰链位置，为满足正交层压板边界条件的场方程；

36、1/4伴随渐进侵彻的背凸变形阶段的正交层压板的应变能为:

37、

38、式中：h为伴随渐进侵彻的背凸变形阶段的正交层压板的厚度，其初始值为h2。

39、1/4伴随渐进侵彻的背凸变形阶段的正交层压板和平头弹的总动能为：

40、

41、式中：μ为正交层压板面密度；

42、拉格朗日值：

43、l＝t-π (8)

44、混合模式失效判据为：

45、

46、式中：j代表与平头弹接触的第j层均质层，随着平头弹的逐层侵彻，取值为1到n；为第j层的最大等效应力，为第j层的等效应力，和分别为第j层的正应力和切应力；

47、拉伸失效判据为：

48、

49、式中：为第j层拉伸应变；

50、与平头弹接触的均质层发生穿透后，伴随渐进侵彻的背凸变形阶段的正交层压板的厚度更新为：

51、h＝h2-jhl   (11)

52、有益效果

53、1、本发明能够预测uhmwpe层压板在平头弹冲击下伴随渐进侵彻的瞬态背凸变形、移动铰传播和弹道极限速度，而不需要使用任何拟合参数和经验公式。

54、2、本发明的预测结果已经通过试验验证，预测结果与试验结果具有较好的一致性，因此本发明所提的方法预测精度较高。

55、3、本发明通过将瞬态分析和拉格朗日法相结合，并引入渐进侵彻失效判据，最终给出了uhmwpe层压板的背凸变形和弹道极限预测。