一种复合管道水击波速的分析计算方法与流程

本发明涉及一种复合管道水击波速的分析计算方法，是一种水工计算方法，是一种用于输水管道工程中对水管重要参数水击波速的计算方法。

背景技术：

1、管道水击波速是分析水击或水力过渡过程的关键参数。早在160多年前，menabrea(1858)就提出了刚性管道、弹性水体条件下的水击波速公式。在间隔40年后，儒可夫斯基(joukowski，1898)考虑管道的弹性，提出迄今常用的薄壁管道的水击波速公式：

2、

3、式中：a为管道水击波速，m/s；k为水体的体积弹性模数，pa；ρ为液体密度，kg/m3；d为管道直径(内径)，m；e为管壁厚度，m；e为管材的杨氏弹性模量，pa。

4、在20世纪70年代，wylie和streeter(1978)考虑了管道支撑情况的影响，对儒可夫斯基水击波速公式进行了修正，同时，在其他人研究的基础上，给出圆形隧洞、带衬圆隧洞和钢筋混凝土管水击波速的公式。与此同一时期，柯莱克提出了混凝土衬砌隧洞的水击波速公式，

5、

6、式中：kc为管道与水接触内壁的弹性系数，即管道内壁抵抗水压变化引起的变形系数；r1、r2、rj、rj+1分别为第1、2、j、j+1层的半径，m；e1、e2、ej、en分别为第1、2、j、n层的管材的杨氏弹性模量，pa；e1为第1层的管壁厚度，m；a2为第2层沿轴向长度l＝1m内的钢筋等效面积，m2；μj、μn分别为第j、n层材料的泊松比；下标j＝1,2,3,…,n为混凝土衬砌隧洞分层编号；n为隧洞分层数，第1层为最里层，第n层为隧洞围岩(最外层)。在式(3)右边：第1项为薄壁钢筒内衬层弹性系数；第2项为混凝土钢筋等效弹性系数，第3项为混凝土衬砌层和水泥灌浆层的弹性系数，第4项为隧洞围岩层弹性系数。柯莱克公式的不足之处是没有考虑隧洞轴向和径向应力对隧洞内衬钢筒和钢筋弹性系数分量的影响。

7、吕海艳(2005)和郭强等(2022)研究了流固耦合，包括轴向应力，对厚壁管道水击波速的影响，结果表明所得管道水击波速值比经典薄壁管道水击波速值小。

8、目前随着对管道防腐蚀和水质要求的提高，已经生产了很多由两个或两个以上的单层管道彼此紧密套合在一起的复合管道，例如预应力钢筒混凝土管(pccp)、钢塑复合管、钢筋混凝土管、带衬隧洞、带衬球墨铸铁管等。周文龙等(2006)针对带内衬和外衬保护的复合管道，采用下述水击波速公式，

9、

10、式中：ep为复合管道的等效弹性模量，pa；d1、d2、d3分别为第1、2、3层的管道直径(内径)；μ1、μ2分别为第1、2层材料的泊松比；e3为第3层的管壁厚度，m。

11、张奥等(2022)总结了常用水击波速公式，对地下铺设带内衬复合管道采用下式，

12、

13、式中：es为土壤的杨氏弹性模量；c1为考虑管道支撑情况的修正系数；e2为第2层的管壁厚度，m。

14、比较柯莱克水击波速公式(2)(3)和带保护层管道水击波速(4)(5)，两者具有一定相似性，式(5)ep相当于取了式(3)kc中第1项和第3项，但式(4)中比式(2)中多了d1e1。另一方面，当令式(3)kc中第1项2rj＝d(管道过水断面直径)和kc中第4项μn＝2.5，则可得式(6)。

15、存在的问题是，如何系统考虑影响复合管水击波速的主要因素，以确定水击波速的理论准确值，以及传统的复合管水击波速公式适用范围。

技术实现思路

1、为了克服现有技术的问题，本发明提出了一种复合管道水击波速的计算方法。所述的方法根据前人的经验，提出了几种计算复合管道水击波速的方法，并明确了其使用范围，并修正了前人错误和一些误解，使复合管道水击波速的计算更加准确，为工程计算提供了更加精确的方法。

2、本发明的目的是这样实现的：一种复合管道水击波速的分析计算方法，所述方法的步骤如下：

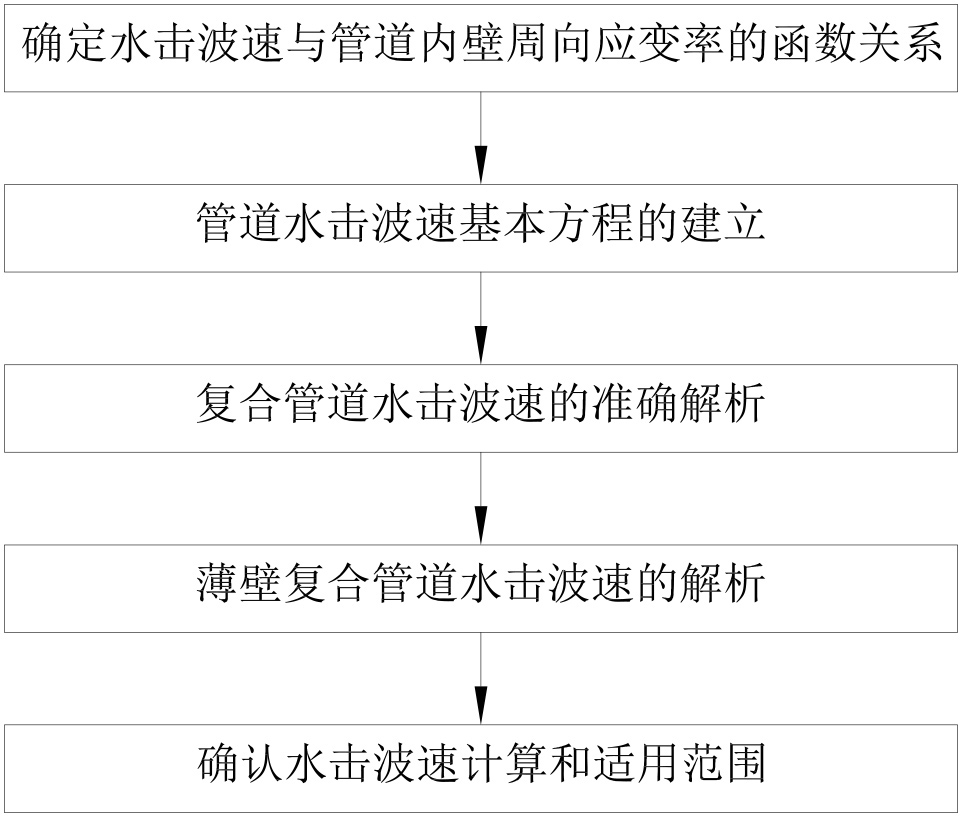
3、步骤1，确定水击波速与管道内壁周向应变率的函数关系：根据水击波速的原始定义，确定水击波速与管道内壁周向应变率的函数关系；

4、输水管道水击波速a的原始定义是：

5、

6、式中：k为水体的体积弹性模数；ρ为液体密度；为管道内壁水压变化率；ai为管道内壁的过水断面面积；为管道内壁的过水断面面积变化率；

7、管道过水断面面积的相对膨胀率：

8、

9、式中：为管道内壁周向应变率；

10、当定义：

11、

12、其中：kc为管道与水接触内壁的弹性系数；

13、则有kc定义下的管道水击波速a0：

14、

15、步骤2，管道水击波速基本方程的建立：建立厚壁圆筒周向应变率与周向、径向和轴向应力变化率的基本方程，并根据管道支撑情况，得到管道内壁周向应变率和外壁周向应变率的基本方程：

16、

17、

18、式中：e杨氏弹性模量；c1为与管道支撑情况有关的常数；ri为管道内壁半径；ro为管道外壁半径；pi为管内壁压强；po为管外壁压强；μ为管道材料的泊松比；

19、对单层厚壁管道，水击波速a1公式：

20、

21、步骤3，复合管道水击波速的准确解析：建立复合管与水接触管壁周向应变率与其它各层应变率、交界面压力、管材力学参数和结构尺寸关系的基本方程，并解析导出准确求解复合管水击波速的通用公式；

22、复合管道是由两个或两个以上的单层管道彼此紧密套合在一起的管道，水击波速a取决于与水接触管壁的周向应变率，即复合管道第1层内壁的周向应变率而不仅与第1层外壁的应变率有关，而且与其它各层内壁和外壁的应变率有关；

23、第j层内壁周向应变率

24、

25、式中：cj为与第j层管道支撑情况有关的常数，j为复合管道的层数编号，j＝n,n-1,n-2,…,1；n为复合管道的层数，是自然数；ej为第j层管道的杨氏弹性模量；ej、ej+1为第j层管道、第j+1层管道的半径；μj为第j层管道材料的泊松比；

26、第j层外壁周向应变率

27、

28、在复合管道第j-1层外壁与第j层内壁的交界面，受水压影响，第j-1层外壁将向外推挤第j层内壁，j-1层外壁产生一周向应变率同时第j层内壁将向内推挤第j-1层外壁，产生一周向应变率从而使两层紧紧挤压在一起，这时在两层交界面的应变率边界条件是：

29、

30、式中：

31、

32、

33、式中：

34、

35、

36、当令式中：

37、

38、在管道水击过程中，取这时取：

39、wn+1＝0

40、

41、其中：wj、wj+1分别为第j层和第j+1层的过渡符号；bj,1、bj,2、bj,3、bj,4分别为与复合管道各层材料的力学特性和结构参数有关的系数；

42、复合管道与水接触内壁的弹性系数kc0：

43、

44、其中：为第一层管道与水接触管壁周向应变率；b1,3、b1,4、w2为复合管道各层材料的力学特性和结构参数有关的系数和过渡符号；

45、综上所述，复合管水击波速的计算程序是：代数递推计算得wn、wn-1、…、w2，然后计算复合管的弹性系数kc0，最后由式：

46、

47、计算水击波速；由于在推导的过程中，全面考虑了复合管影响周向应变率的各因素，所以由此计算的水击波速是准确解；

48、步骤4，薄壁复合管道水击波速的解析：对薄壁复合管与水接触管壁周向应变率各因素解析，提出水击波速的解析公式，包括薄壁衬砌隧洞和地下埋管的水击波速的解析公式；

49、薄壁复合管道通用弹性系数kc1：

50、

51、薄壁复合管道的水击波速a1：

52、

53、薄壁衬砌隧洞弹性系数kc2：

54、

55、薄壁衬砌隧洞的水击波速a2：

56、

57、地下铺设管道内壁的弹性系数和水击波速分别为：

58、

59、

60、式中：en为回填土的弹性模量；cs为经验系数；

61、步骤5，确认水击波速计算和适用范围：

62、方法1，对于含有厚壁层的复合管道，包括衬砌采用复合管道通用水击波速公式：

63、对于含有厚壁层的复合管道，包括衬砌，采用如下的水击波速公式确定水击波速：

64、

65、厚壁层的复合管的弹性系数kc：

66、

67、

68、方法2，对于薄壁复合管道，采用薄壁衬砌隧洞水击波速公式：

69、薄壁衬砌隧洞弹性系数kc2：

70、

71、薄壁衬砌隧洞的水击波速a2：

72、

73、本发明的优点和有益效果是：本发明首先根据水击波速的原始定义，建立了水击波速与管道内壁周向应变率的函数关系，以及周向应变率与周向、径向和轴向应力变化率的函数关系。然后，考虑了复合管各层应变率、交界面压力、管材力学参数和结构尺寸等各方面因素，解析导出准确计算水击波速的通用公式。在此基础上，对影响薄壁复合管水击波速的各因素解析，导出水击波速的解析公式，包括薄壁衬砌隧洞和地下埋管的水击波速公式，并与传统的复合管水击波速公式进行了对比分析。本发明明确不同种复合管道的弹性系数和水击波速，从而使水击波速的计算更加精确，为工程设计提供了更加科学的计算方法。