三维边坡滑面智能搜索方法

本发明涉及边坡数值计算领域，具体涉及一种三维边坡滑面智能搜索方法。

背景技术：

1、岩/土边坡的破坏通常会导致严重的后果，如人员伤亡和经济损失。因此，有必要对边坡进行稳定性分析，以预测边坡的关键破坏面和安全系数，两个边坡稳定性评价与设计中最重要的指标。在过去的几十年中，随着工程建设和防灾减灾的需求，已经发展了许多用于边坡稳定性分析的方法，包括试验方法、数值方法和极限平衡方法等。

2、但是，现有技术中，试验方法评价边坡稳定性效果有限，数值方法和极限平衡方法主要集中在二维边坡分析，三维分析方法限制较多，例如三维极限平衡方法限制滑面为椭球，例如论文：张锟等2017.自适应差分进化算法在边坡滑面搜索中的应用.岩土力学38,1503–1509.而强度折减方法需要大量迭代弹塑性计算，时间消耗较大，例如学位论文：张亚军,2024.基于三维数值流形法的边坡稳定性分析(硕士).海南大学)，人工和时间成本均较高，很难大规模应用。

技术实现思路

1、有鉴于此，本发明提供了一种三维边坡滑面智能搜索方法，能够用于三维边坡滑面智能搜索与稳定性评价。

2、具体，通过如下方案实现：

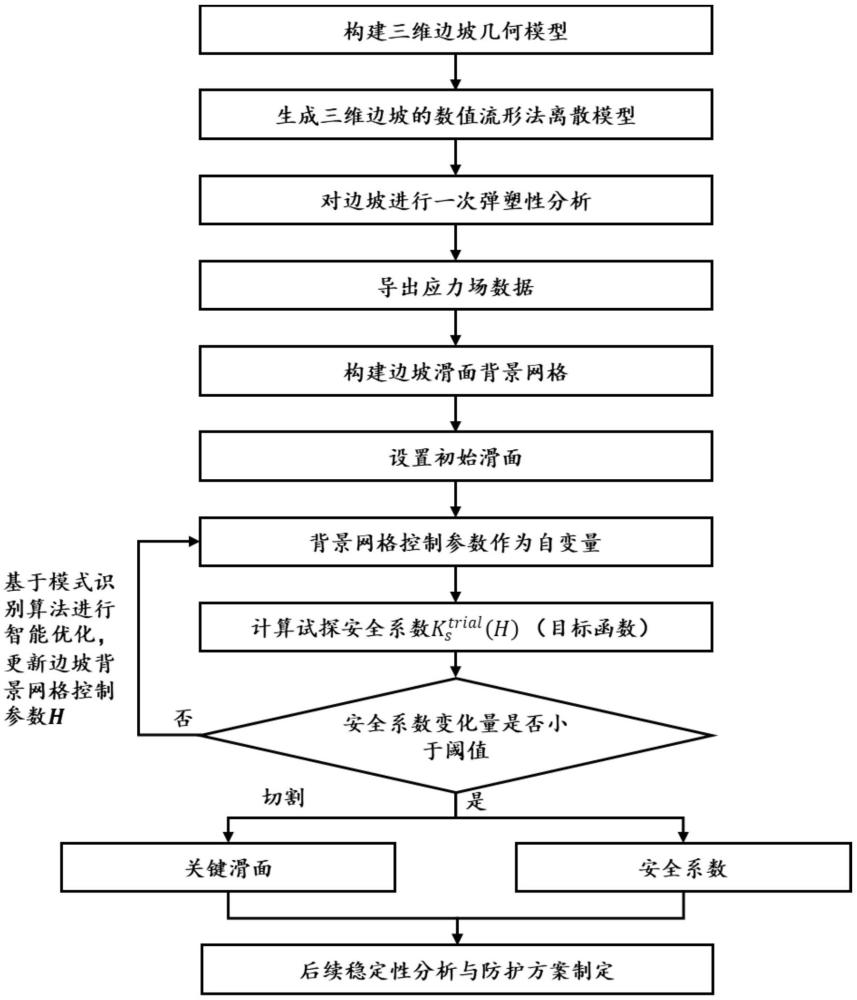
3、三维边坡滑面智能搜索方法，包括以下步骤：

4、步骤s1:构建需要分析区域的三维边坡几何模型；

5、步骤s2:对三维边坡分析区域进行物理网格划分，生成三维边坡的离散模型，并对边坡进行材料分组和边界面分组，为数值分析做准备；

6、步骤s3:根据边坡材料参数设置边界条件，使用数值流形法对边坡模型进行一次弹性或者弹塑性分析，并导出应力场数据和材料场数据，为后续计算安全系数做准备；

7、步骤s4:构建边坡滑面的背景控制网格，对背景控制网格与坡体进行布尔运算，裁剪掉多余的部分，生成初始试探滑面；

8、步骤s5:以背景控制网格的控制参数作为自变量，以试探滑面的试探安全系数为目标函数，计算试探安全系数。为确保背景网格的形状合理性，避免生成的试探滑面明显局部上凸或下凹，在目标函数中加入约束条件；

9、步骤s6:基于模式搜索算法进行智能优化，更新边坡滑面控制参数并计算试探安全系数，当试探安全系数变化量小于设定阈值时模式搜索算法收敛，最终得到关键滑面和对应的安全系数。

10、进一步优化，所述步骤s3中采用数值流形法计算边坡模型弹塑性应力场，具体包括如下步骤：

11、步骤s3.1：定义三维边坡分析区域ω静力学弹塑性问题的基本控制方程和边界条件；其中，基本控制方程为:

12、σij,j+bi＝0,inω；

13、上式中，σij表示柯西应力张量，σij,j表示对σij求空间偏导，bi表示体荷载向量，i代表该应力的方向，j代表该应力所在面的外法线方向，ω表示三维边坡的分析区域。

14、边界条件为：

15、

16、上式中，代表位移边界作用区域，代表应力边界作用区域，ui代表位移矢量，表示位移边界上的给定位移向量。σij表示柯西应力张量，nj代表应力边界的外法线方向，表示应力边界上的指定牵引力，i代表该应力的方向，j代表该应力所在面的外法线方向；

17、数值流形法在第γ个流形单元meγ上的全局位移近似函数是权函数wkγ(x)和覆盖函数ukγ(x)的内积，表示为：

18、

19、数值流形法物理片ppk的权函数wkγ(x)一般满足以下三个条件：

20、

21、0≤wkγ(x)≤1,if x∈ppk,

22、

23、其中，当流形单元meγ被物理片ppk覆盖时，权函数wkγ(x)的范围为0-1，反之不被覆盖时，权函数为0。定义流形单元meγ的八个物理片上都覆盖该流形单元，它们的权函数都满足0≤wkγ(x)≤1，且和为1。

24、覆盖函数ukγ(x)可以使用任意阶次的多项式函数构建，本发明使用0阶多项式函数作为权函数以避免线性相关问题。结构化六面体网格被用来构建数学覆盖系统，因此采用八节点六面体单元的形函数来构建权函数wkγ(x)。

25、数值流形法全局位移近似函数可以表示为紧凑形式如下：

26、

27、其中nγ称为形函数矩阵，dk是一个包含与上述八个物理片相关的全部自由度的列向量，这八个物理片它们被用来形成这个流形单元meγ。

28、步骤s3.2：根据控制方程和对应的边界条件，得到弹塑性问题的如下函数i(u)：

29、

30、步骤s3.3：由于数值流形法中数学覆盖系统通常不与物理网格匹配，上的位移边界条件通常无法直接满足；通过罚函数法施加位移边界条件，对应的上述函数修正为：

31、

32、上式中，α1为对应于位移边界条件罚参数；

33、令δi*(u)＝0，则弹塑性问题的系统平衡方程写为如下矩阵形式：

34、kd＝f；

35、其中，d是全局位移向量，k和f是广义整体刚度矩阵和力向量；

36、

37、上式中，n和b分别表示形函数矩阵和应变矩阵，dep表示弹塑性矩阵；b＝ldn；算子ld为：

38、

39、现有技术中的不同于强度折减方法需要大量重复的弹塑性分析计算，而本发明只需要对边坡在重力作用下进行一次弹塑性计算即可。此时边坡强度参数没有折减，边坡往往不处于临界状态，弹塑性分析的迭代次数一般不会很大，计算消耗较小。对边坡进行一次弹塑性计算后，导出边坡应力场，后续步骤在边坡应力场的基础上，插值可以获得边坡体内部任意一点的应力状态。

40、进一步优化，在三维边坡几何信息基础上，构建三维边坡滑面。三维边坡滑面的位置和形状具有很多种可能性，最常见的三维滑面构造方式为椭球形，但这种滑动面过于理想，无法描述复杂滑面。因此为了模拟任意三维滑面可以采用一系列控制点经样条曲面拟合或插值得到。

41、本发明步骤s4利用背景网格来模拟任意形状的三维边坡滑面，具体包括如下步骤：

42、步骤s4.1:定义边坡滑面的背景网格，将背景网格上所有节点x、y坐标轴方向的坐标固定，z坐标轴方向的坐标作为变量，得到三维边坡滑面背景网格的控制参数组成的列向量h，为：

43、

44、上式中，θ表示控制点的数量，hβ表示第β个控制点的高度，即第β个控制点在z坐标轴的值；

45、步骤s4.2:对背景控制网格与坡体进行布尔运算，裁剪掉多余的部分，生成计算安全系数所需的试探滑面。

46、根据h确定的三维边坡滑面不一定是合理的，例如滑面不能出现局部突变，明显上凸或下凹，可通过手动剔除的方法删除此类不合理的滑面，但该做法效率明显较低。例如论文：林永生等,2013.基于有限元计算的边坡三维滑裂面搜索.岩土力学34,1191–1196，记载了采用控制点生成的滑面虽然可以比较真实地模拟实际的滑裂面，而且还能够模拟任意形状的滑裂面。但是由控制点生成的滑裂面就有明显的局部上凸和下凹现象，根据这个模拟的滑裂面计算得的安全系数可能会偏大。

47、为了实现三维边坡滑面的自动搜索，需要给定适当的约束条件，避免滑面的明显的局部上凸或下凹。最常见的做法为提前假定三维滑面形状为外凸的几何形状，例如中国专利cn201610116074.0，一种边坡三维临界滑裂面搜索方法，直接采用椭球方程作为临界滑裂面假定形状；论文张锟等，2017.自适应差分进化算法在边坡滑面搜索中的应用.岩土力学38,1503–1509.以对椭球方程进行修正以描述三维滑面。上述方法对滑面形状进行了假定，失去了滑面形状的任意性，不太符合真实情况。

48、为了定义边坡滑面的形状约束条件，对于二维滑面，论文：刘高扬等,2017.基于独立覆盖流形方法与矢量和方法的边坡稳定性分析.岩石力学与工程学报36,1434–1442，记载了可以通过控制各控制点的坐标和各直线段的斜率来实现，但是该方法无法应用于三维滑面形状约束。

49、为此，本发明所述步骤s5中，加入了三维边坡滑面的形状约束条件，具体按照如下步骤设定：

50、步骤s5.1：限定滑面局部都向着坡体方向凸出，即对于滑面上任意一个三角形单元所在平面，其法向方向指向坡体，滑面上其他点都位于该平面的正半平面。

51、设定第个局部约束对应的三角形单元三个顶点分别为和约束点三角形法向方向计算为：

52、

53、其中为:

54、

55、滑面上其他点到这个三角形单元所在平面的距离必须大于等于0，因此存在以下局部约束方程：

56、

57、去掉分母，得到：

58、

59、带入点和坐标值，将局部约束方程写为矩阵形式：

60、

61、其中，则有：

62、

63、

64、步骤s5.2：根据步骤s5.1中局部约束方程构建整体约束方程：

65、ah≤0

66、其中，a为不等式约束矩阵，通过将各个局部约束方程中的矩阵组装得到；h为各个控制点高度组成的向量，通过将各个局部约束方程中的矩阵组装得到。

67、进一步优化，所述安全系数通过如下步骤计算：

68、基于数值流形法弹塑性分析获得的三维边坡应力场基础上，获得所述试探滑面s上任一点g受力状态；设定点g处应力张量为σg，为试探滑面上该点g处切平面的单位法线方向，指向滑体方向为正，则求得滑体上点g对边坡体的作用力试探滑面上点g处滑体对坡体的法向和切向作用力和以及试探滑面上点g处坡体对滑体的抗滑法向应力为：

69、

70、根据摩尔库仑强度准则,滑面上任一点边坡体对滑体的极限抗滑剪应力为：

71、

72、其中，c为边坡岩土体的粘聚力参数，φ为边坡岩土体的内摩擦角参数，为试探滑面上点c处的坡体潜在滑动方向，

73、基于滑面上各点的抗滑剪应力矢量，在滑面上进行积分，获得坡体对滑体的极限抗滑剪应力合力为：

74、

75、根据极限抗滑剪应力合力确定全局的主潜在滑动方向

76、

77、除了剪应力，边坡体对滑体的抗滑力矢量还包括法向应力部分，滑面上任意一点g处边坡体对滑体的抗滑力矢量为:

78、

79、滑面上任意一点g处滑体对边坡体的作用力为也就是滑体在滑面上任意一点g处的下滑力为将抗滑力和下滑力向着全局的主潜在滑动方向进行投影，并在整个滑面上进行积分，获得边坡的试探安全系数：

80、

81、上式中，表示坡体对滑体的抗滑力合力在主潜在滑动方向上的投影，表示滑体的下滑力合力在主潜在滑动方向上的投影，表示滑体主潜在滑动方向，表示滑体上任一点的下滑力，表示滑面上任意一点处边坡体对滑体的抗滑力。

82、进一步优化，各个局部约束方程中的矩阵按照如下方式组装得到a：

83、对于第个约束方程，涉及到点为和编号为对应的控制点高度为

84、设定，

85、

86、则，将列向量中的所有元素作为不等式约束矩阵a第行，第列的元素，也就是除此之外，不等式约束矩阵a第行其他列的值为0。将列向量中的所有元素作为矩阵h第行的元素；

87、同理，将其他约束方程矩阵中元素按照上式代入，得到最终的不等式约束矩阵a。

88、进一步优化，基于模式搜索智能算法进行滑面搜索实际上是一个优化问题，为了考虑不等式约束条件，一种做法是利用罚函数方法将不等式约束条件添加到目标函数中去。但是该方法由于罚参数取值不存在物理意义，需要手动调整，实际效果并不好。为此，本发明所述步骤s6对模式搜索智能算法的流程进行改进，将不等式约束条件的满足添加到优化流程中去，来增加算法的鲁棒性和效率，具体包括如下步骤：

89、步骤s6.1：从给定的初始滑面控制参数h0开始，依照所有θ个控制点的z坐标轴e1,e2,…,eβ,…,eθ方向，用指定步长δk进行试探移动；每次选择一个自变量hβ，只对其进行移动，此时eβ＝[0,0,…,1,…,0]，只有第β项为1，其余为0，即就是每一次移动一个背景网格控制点；

90、步骤s6.2：对于第β个控制点沿z坐标轴方向进行如下移动探测，此时除去hβ外其他自变量不会移动，因此为已知值，则有：

91、

92、即，将列向量中的所有元素作为不等式约束矩阵a第行，第列的元素，即除此之外，不等式约束矩阵a第行其他列的值为0；表示第个约束条件对应的行号。

93、步骤s6.2.1：将除hβ外其他的变量移动到不等式右侧，得到只有一个变量hβ的不等式方程组，如下式所示：

94、

95、由此，计算出hβ的取值范围为后面进行探测确定了可行的探测区域。

96、步骤s6.2.2：判断是否大于等于

97、如果是，则此时第β个控制点不可移动；

98、如果否，则进行如下移动探测：首先进行正方向探测，在hβ的取值范围内，移动h到h+eβδk，计算出(h+eβδk)对应的试探安全系数如果说明探测成功，取h＝h+eβδk；反之探测失败，再进行反方向的试探，具体为：在hβ的取值范围内，移动h到h-eβδk，计算出(h-eβδk)对应的试探安全系数如果说明探测成功，取h＝h-eβδk，反之探测失败，h保持不变；

99、步骤s6.3：按照第β个轴方向的探测方法，遍历所有的背景网格控制点高度，反复试探优化；

100、步骤s6.4：当一轮试探结束时，减小步长δk重复步骤s6.2、s6.3继续进行迭代优化，直至试探安全系数变化量小于设定的第一阈值，或步长δk小于设定的第二阈值时算法收敛，得到安全系数和关键滑面；如果达到最大迭代次数还未收敛，则调整参数δk或重新布置背景网格进一步计算。

101、与现有技术相比，本发明具有如下有效益效果：

102、本发明以三维边坡为例，其不仅考虑天然坡体内部真实的应力场分布，且只需要进行一次弹塑性分析。同时还具有更通用的破坏面形状，能够更灵活的搜索三维边坡的安全系数和关键滑动面，基于已有的智能优化算法自动搜索三维边坡的关键滑面,为稳定性评价与设计提供参考，能够为减少与边坡破坏相关的地质灾害提供理论支持。