一种基于门控图神经网络的供水管网水力状态预测方法

本发明属于城市供水领域，涉及一种基于门控图神经网络(gated graph neuralnetwork，ggnn)的供水管网水力状态预测方法。该方法旨在利用智能化的图神经网络技术，提高供水管网水头预测的精度和可靠性，适用于智能水务管理、漏损检测、管网优化控制等应用场景。

背景技术：

1、城市供水管网是现代城市基础设施的重要组成部分，负责向居民和工业用户提供清洁、稳定的饮用水。然而，随着城市规模的不断扩大，供水管网的复杂性也逐渐增加，导致管网中的水压呈现显著的时空变化。这种变化可能会引发管网的破裂、漏损等问题，严重影响水质和供水系统的安全性。因此，及时、准确地预测供水管网的水力状态对于保障供水系统的安全、高效运行至关重要。

2、传统的供水管网水力预测主要依赖于水力模型，但这些模型在校准过程中需要精确的物理参数，如管道粗糙度和节点需水量，这些参数很难直接测量。节点的需水量会随着时间的推移发生变化，受诸多因素影响，如季节变化、居民用水习惯和工业需求。而管道粗糙度也会随着管道的老化和沉积物的积累而变化，给水力模型的校准带来了极大的挑战。此外，传感器的部署成本限制了监测点的数量，导致数据覆盖不足，使得基于传统水力模型的水力状态预测变得更加困难。

3、针对传统方法的局限性，基于元模型的预测方法近年来逐渐受到关注。元模型利用机器学习技术，通过学习历史数据和网络结构信息(如管道直径、材料、管龄等)，实现了以下优势：(1)无需复杂校准：元模型基于数据驱动，避免了对物理参数的繁琐校准，能够快速适应动态变化；(2)无需复杂校准：元模型基于数据驱动，避免了对物理参数的繁琐校准，能够快速适应动态变化；(3)适应性强：元模型尤其适合传感器稀缺或部署成本高的场景，展现出较强的环境适应能力。通过利用元模型，可以减少对物理模型的依赖，为供水管网的运行管理提供了更灵活、高效的技术手段。

4、尽管元模型具有巨大的潜力，但在实际应用中仍面临若干挑战。元模型的训练过程中，通常需要对整个管网的所有节点进行误差估计，这对于大规模管网尤其具有挑战性，因为这些网络的传感器覆盖通常有限，缺乏足够的全局水力数据。如何高效地从稀疏数据中提取有用信息并转化为可靠的预测，仍是亟待解决的关键问题。

技术实现思路

1、本发明针对现有技术中的不足，提出了一种用于供水管网的基于门控图神经网络(ggnn)的水压预测方法，本发明通过引入传感器初始化策略和松散的物理约束，能够在稀疏监测数据条件下对管网中各节点的水头进行高效预测。本发明的主要特点在于，针对稀疏传感器布设带来的数据缺失问题，提出了一种基于网络拓扑信息的初始化策略。这一策略不仅减少了数据缺失对预测精度的影响，还显著提高了模型的收敛速度。通过结合水力学的物理约束条件，使得模型能够更好地反映管网节点间的水力关系，提高整体预测的准确性。

2、为了达到上述的目的，本发明采用的技术方案为：

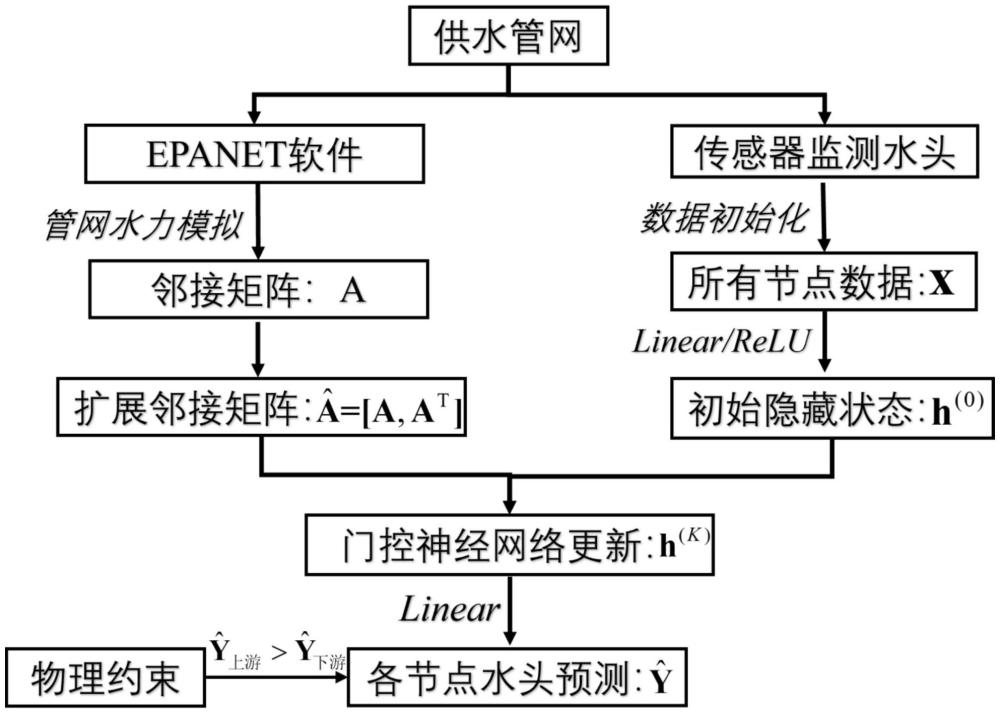
3、一种基于门控图神经网络的供水管网水力状态预测方法，所述的供水管网水力状态预测方法首先，利用传感器节点监测的水头数据初始化其他没有布置传感器的管网节点的数据；其次，抽象出供水管网的拓扑结构，并构建有向图的管网邻接矩阵；最后，基于管网邻接矩阵和初始化后的节点水头信息，构造基于ggnn的水头预测模型，对供水管网中所有节点的水头进行预测。具体包括以下步骤：

4、步骤(1)初始化未监测节点的水头数据；

5、在供水管网中，由于成本限制，只能在较少的管网节点上布置传感器来监测节点的水头信息，期望利用布置传感器的管网节点历史tc时间步监测的水头数据，预测未来tp时间内管网中所有管网节点(包括有传感器监测的和没有传感器监测的节点)的水头值。

6、为了在传感器数据稀少的情况下预测供水管网所有节点的水力状态，节点值的初始化起着至关重要的作用。对于没有监测的节点，必须分配一个有意义的初始值，以确保模型能从所有管网节点中学习，而不仅仅是有传感器监测的管网节点。在以前的方法中，常见的做法是用默认值(如零)来填充这些没有传感器监测的节点值。然而，这种方法没有考虑到管网的动态行为，忽略了初始化过程中应遵循的时空相关性。这种方法可能导致模型预测的没有传感器监测的管网节点的水头值保持不变，或无法显示真实世界系统中观察到的自然波动。

7、为了克服这一局限性，本发明提出了一种基于最短路径距离的新型初始化策略，该初始化策略将供水管网抽象为图结构g＝(v,e)，其中v是所有管网节点集合(|v|＝n,n表示供水管网节点个数)，边集合e表示节点之间的连接关系。在供水管网中，水库、水箱和用水节点可以表示为节点，而连接它们的管道、阀门和泵可以表示为边。为此，首先计算出一个距离矩阵，用于测量图结构中每一个没有布置传感器的管网节点p与每一个布置传感器监测的管网节点s之间的最短路径距离，这个距离不是基于现实世界中的物理距离，而是基于连接节点的边的数量。采用迪杰斯特拉(dijkstra)算法确定上述的最短路径距离，并将最短路径距离的倒数作为权重来分配每一个传感器节点对没有布置传感器的节点的影响。节点值的初始化是以传感器值的加权平均值计算的，其中权重由最短路径距离的倒数决定：

8、

9、其中，s是布置了传感器的管网节点的集合，s表示集合s中的第s个布置传感器的管网节点；dp,s是没有传感器监测的管网节点p距离布置传感器监测的管网节点s的最短距离；xp和xs分别表示历史tc时间步内没有传感器监测的管网节点p初始化后的水头以及布置了传感器的管网节点s监测的水头信息。

10、这种初始化方法可确保未受监测的管网节点接收到受附近传感器数据影响的数值，从而反映供水管网的空间动态，使模型更好地捕捉水头的时间波动。

11、步骤(2)建立图神经网络模型；

12、步骤(2.1)首先，图神经网络模型中的每个节点v(包括有传感器监测的和没有传感器监测的节点)都与一个属性特征向量xv相关联，该属性特征向量表示从步骤(1)数据初始化步骤中获得的tc时间步内的初始水头值(没有传感器监测的管网节点则为初始化后的水头值，有传感器监测的管网节点则为其实际监测的水头值)，初始的水头值作为节点的属性特征。为了提高这些属性特征的表达能力，采用线性变换将管网节点的属性特征投影到一个大小为m的高维隐藏空间中：

13、

14、其中，是管网节点v的初始隐藏状态，这个作为后续图神经网络第一次迭代的初始条件；w0和b0是神经网络层的权值和偏置项；relu是线性整流单元激活函数。

15、步骤2.1允许图神经网络模型捕捉节点属性之间的非线性关系，并扩展特征空间，从而促进更复杂的表征。m表示隐藏状态的维度大小，它直接影响图神经网络模型的表示能力。较大的m值可以提升模型学习和表达复杂函数的能力，从而提高其在训练集和测试集上的表现。然而，过大的m值可能带来过拟合风险，并增加训练的复杂性，导致更高的计算资源消耗和更长的训练时间。因此，在实际应用中需要在图神经网络模型性能和计算成本之间进行权衡。综合考虑这些因素，本发明经验性地选择了m＝128。

16、步骤(2.2)对于一个供水管网，其抽象出来图结构可以是有方向的有向图(方向代表水流在管道中的流动方向)或者是没有方向的无向图(不考虑水流的流动方向)。供水管网的连通性由邻接矩阵a表示，该邻接矩阵可用于有向和无向边。邻接矩阵的元素auv表示任意管网节点u和v之间的关系。对于有向图，auv表示节点u到节点v之间是否存在流量以及流量的方向。对于无向图，邻接矩阵是对称的，邻接矩阵a中的元素表示两个节点间是否有管道连接。边权重可以表示管道长度、直径或流量容量等属性。为了包含不同类型的权重，可以用连续值来定义邻接矩阵，以反映边的具体特性：

17、auv＝wuv      (3)

18、其中，wuv表示分配给节点u和v之间边的权值，这种灵活性使模型能够利用网络拓扑和边属性中的附加信息；auv是邻接矩阵a中第u行第v列的值。在本发明中，根据经验以及数据易获取性选择了基于有向图的二元权重(0-1)，权重的配置是根据节点u与节点v之间的管段是否存在水流流动来决定的。具体来说如果管段直接连接节点u和节点v，并且水流从节点u向节点v流动，则该有向边的权重设为1；如果不存在直接连接或水流方向相反，则权重设为0。这种方法清晰地表达了管网中每个管段的水流状态和方向性。

19、步骤(2.3)为了捕捉双向信息流并同时考虑传入和传出的边，本发明通过添加邻接矩阵的转置来扩展邻接矩阵：扩展后的邻接矩阵确保图神经网络模型考虑到沿边的双向信息传播，从而增强了从供水管网图结构中学习的能力，无论图结构是有向图还是无向图。

20、通过步骤2.1得到的节点初始隐藏状态需要传入门控图神经网络ggnn中进行信息的更新迭代，其中上述步骤2.1中的表示管网节点v的第一次迭代的隐藏状态。在门控图神经网络ggnn的第k次迭代中，每个节点v的隐藏状态都会通过两个主要步骤进行更新：聚合和传播。具体如下：

21、在聚合步骤中，每个节点利用扩展后的邻接矩阵从其邻居那里收集信息。节点v的聚合信息计算公式为：

22、

23、其中，ν(v)表示节点v的相邻节点集，q是节点v的相邻节点集ν(v)中包含的节点；是节点v和u对应的扩展后的邻接矩阵的元素；是上一次迭代中节点v的相邻节点q的隐藏状态；ba是偏置向量。这一步骤允许每个节点根据扩展邻接矩阵中的连接性加权，纳入来自其近邻的信息。

24、聚合后，传播步骤使用门控递归单元(gru)更新每个节点的隐藏状态，该门控递归单元捕捉时间依赖性并控制信息流。更新方程如下：

25、

26、

27、其中，和分别是节点v在迭代k次时的更新门和重置门；wr和ur分别是公式(5)中的神经网络层的可学习权重和偏置；wz和uz是公式(6)中的神经网络层的可学习权重和偏置；w和u分别是公式(7)中的神经网络层的可学习权重和偏置；σ(·)是sigmoid激活函数；⊙是元素乘法。这种gru传播机制使模型能够有选择地整合来自聚合信息的新信息，同时保留先前隐藏状态的基本方面。这种选择性更新使模型能够有效捕捉网络中的近期变化和历史模式。

28、对于管网中任意节点，上述的迭代过程共进行k次，最终输出节点的最终隐藏状态。对于节点v，表示通过k次迭代后节点v的最终隐藏状态。

29、通过k次的聚合和传播步骤，ggnn可以迭代更新和完善节点状态，将节点之前的表示及其邻近节点的信息纳入其中。这种迭代过程捕捉了图结构中的动态和交互，使ggnn能够学习节点之间的复杂关系和依赖关系。迭代次数k的数量决定了ggnn的信息传播深度。当k＝1时，每个节点只能向其近邻学习。随着k的增加，ggnn可以从k步以外的节点获取信息，包括间接连接。k的选择会影响模型的学习能力和效率。k值越大，计算复杂度和内存使用量就越高，而k值越小，模型捕捉必要依赖关系的能力就越有限。因此，选择合适的k值需要在模型性能和计算效率之间取得平衡。根据经验，传播步k取5时能得到较好的效果。

30、步骤(2.4)将步骤(2.3)更新得到的v节点的最终隐藏状态通过线性层转化生成图神经网络模型最终的预测水头信息，

31、

32、其中，是节点v的输出向量，在本发明中，图神经网络模型预测未来tp时间范围内的水力状态，为节点v未来tp时间内的预测水头值。wo和bo分别是神经网络的输出权重矩阵和偏置向量；表示的是通过上述步骤2.3迭代k次后的节点v的最终隐藏状态。

33、步骤(3)训练基于ggnn的水头预测模型；

34、本发明的一个主要特点是在水头预测模型训练过程中加入物理约束。这些物理约束条件确保水头预测模型的预测结果符合供水管网的已知物理规律，例如上游节点的水头必须大于下游节点的水头。

35、所述的水头预测模型的核心损失函数由两部分组成：1)预测损失，用于衡量监测传感器节点预测水头的准确性；2)物理惩罚项，用于执行水力约束条件，即水头应从上游节点向下游节点递减。

36、步骤(3.1)预测损失计算为监测节点的预测值与观测值之间的平均绝对误差(mae)：

37、

38、其中，s是布置了传感器的管网节点的集合；s表示集合s中的第s个布置传感器的管网节点；和ys分别是布置传感器的管网节点s对未来tp时间内的水头预测模型预测的水头和传感器监测的水头。

39、步骤(3.2)物理惩罚项强制执行水流条件，即对于任何一对相连的节点i和j，节点j(下游)的水头必须小于或等于节点i(上游)的水头。表达式为：

40、

41、其中，e是边的集合，和分别是节点i和j的预测水头值(i，j特指的是边集合e中的任意一条边上的两个节点，且水流从节点i流向节点j。上述步骤2中涉及的节点u，v为管网中任意的节点)。该项旨在惩罚任何违反预期水流量的预测。即使在无向图中，每个节点既可以是其他节点的上游，也可以是其他节点的下游，这一物理约束仍然可以应用。对于无向图，这种二元性有助于模型学习整个网络中水头值的平滑过渡。

42、步骤(3.3)最终的损失函数ltotal是预测损失与物理惩罚之和：

43、ltotal＝lprediction+λlpenalty(12)

44、其中，λ是一个超参数，用于控制惩罚项的相对重要性。这种计算方法确保了模型在预测准确性和物理一致性之间取得平衡，从而提高了预测的可靠性。本发明中所述的λ范围为0.5～1.5。

45、利用公式(12)训练后最终得到水头预测模型。

46、步骤(3.4)本发明提出的上述步骤3中训练后的水头预测模型，利用步骤1中布置传感器的管网节点历史tc时间步监测的水头数据，预测未来tp时间内管网中所有管网节点

47、步骤(3.5)为了评估水头预测模型的预测准确性和可靠性，本发明采用了两种评价指标：平均绝对误差(mae)和纳什系数(nse)。这两个指标能够从不同的角度提供关于模型性能的互补性信息。

48、mae指标用于衡量预测水头值与真实水头值之间的误差的平均幅度，不考虑误差的方向。mae的计算公式为：

49、

50、其中，n表示所有节点和时间步的预测总数，和y分别是预测水头和真实水头值。mae为一个直观的误差幅度度量，能够在与预测变量相同的单位下直接反映模型的预测精度。

51、纳什系数是一个标准化的统计量，用于评估模型预测的精度，相较于观测数据的变异性。其计算公式为：

52、

53、其中，为所有样本的真实水头值的均值。nse的取值范围从-∞到1，其中nse为1表示完美预测，nse为0表示模型预测与数据均值相等，nse为负值表示模型的预测效果不如均值预测。

54、通过采用mae和nse两个评价指标，本发明能够从不同角度全面评估模型的性能。mae侧重于衡量预测误差的平均幅度，突出预测与真实值之间的实际偏差；而nse则评估模型预测与真实数据变动的一致性，反映模型捕捉水头变化规律的能力。

55、本发明的有益效果包括：

56、(1)本发明能够提高水头预测准确性：通过结合基于传感器的初始化策略和物理约束，本发明显著提升了水头预测模型在不同供水管网中的预测准确性。该方法能够有效降低了mae，并提高了nse。

57、(2)本发明适应性强：本发明的ggnn模型展现出了在各种不同配置的供水管网中都能有效适应的能力。这种适应性不仅减少了对复杂调优的依赖，还为不同规模、不同结构的管网提供了一个统一的预测框架。这一特点使得该ggnn模型能够广泛应用于各类水力管网的管理，推动了水务行业的智能化发展。

58、(3)本发明能够提高实时监测和决策支持能力：本发明的水头预测模型为实时监控和管网管理决策提供了可靠高效的解决方案。它通过集成基于传感器的初始化、物理约束和有向图表示，为稀疏传感器数据条件下的水力预测精度提供了有效提升。这一框架为供水管网中的实时预测提供了新的工具，能够更好地进行管网运行监控和调度优化。