基于密度峰值聚类改进围绕中心点划分算法的供水管网压力监测点布置方法

本发明属于城市供水管网设计，涉及管网布点监测，尤其涉及一种基于密度峰值聚类改进围绕中心点划分算法的供水管网压力监测点布置方法。

背景技术：

1、市政供水管网由管道、配件和附属设施组成，是保证一个城市经济发展和生活水平的重要基础设施，是城市生存和发展的生命线。但是由于城市用水量的不断增加和管网使用年限的增长，市政供水管网逐渐暴露出较大范围的漏损情况，如不及时处理，会出现爆管等安全事故，造成水资源的浪费和经济损失。

2、为了保障给水管网安全运行，实现给水管网优化调度，首先需要一定数量的监测点对整个给水系统的运行信息进行采集，通过处理、分析由优化后的监测点采集到的管道数据，能有效全面地反映管道运行状态。采集的数据必须既具有准确性又具有代表性，采集的数据的代表性，即监测点数量及位置问题，给水管网监测点布置方案直接影响到监测点监测数据的质量。所以，在建立给水管网模型之前必须先确定给水管网监测点优化布置方案，以最少监测节点覆盖整个监测区域。

3、压力监测点布置方法发展至今，按其发展过程可分为人工经验法和理论分析法两大类，具体介绍如下：人工经验法，是管理者基于对供水管网的熟悉掌握进行手动布置压力监测点，经验布置法的对象大多为简单的小型供水管网且布置较为主观，运用经验法选取的监测点布置方案往往会因为监测点的位置和数量之间的数学关系不匹配，其布置方案往往缺乏相应的合理性，只能提供供水管网大概的调度信息和基本的水力运行信息。并且对于结构复杂的大型环状管网由于依靠经验并无法完全熟知全部管网的运行状况，所以经验布置法已不能满足大型供水分区的需求；近年来，国内外的研究学者尝试将理论分析法引入到压力监测点布置中来。理论法布置优化压力监测点主要是将供水系统节点的某些水力特性作为约束条件或控制指标，构建相关目标函数或特性矩阵，通过遗传算法、蚁群算法、回归分析、非线性映射理论分析等算法或分析手段对目标函数或特性矩阵进行求解分析求解，从而得到相应的压力监测点布置方案。

4、申请号为202010053680.9的发明专利公开了一种基于cfsfdp聚类算法的给水管网压力监测点布置方法。使用模拟软件构建管网模型，在管网模型上密集布设压力监测点，记录所有压力监测点的坐标；分别为管网模型配置正常工况和漏损工况，获取所有压力监测点在不同工况下的压力数据，计算每个压力监测点的压力影响度和差异系数；利用压力监测点的坐标、压力影响度和差异系数构建原始数据集，将原始数据集输入cfsfdp算法，得到聚类结果；以所有的聚类中心作为压力监测点的布置位置。

技术实现思路

1、为解决上述技术问题，本发明提出了一种基于密度峰值聚类改进围绕中心点划分算法的供水管网压力监测点布置方法，基于dpc算法可以避免pam算法中选出的初始聚类中心过于相近而导致聚类结果的不稳定，同时也避免了在同一簇中选择多个初始聚类中心而忽略数据对象较少的簇，进而确认当前聚类中心数目下的最优压力监测点布置方案，在更贴近真实供水管网特性的同时提高了后续压力监测点布置的可靠性。

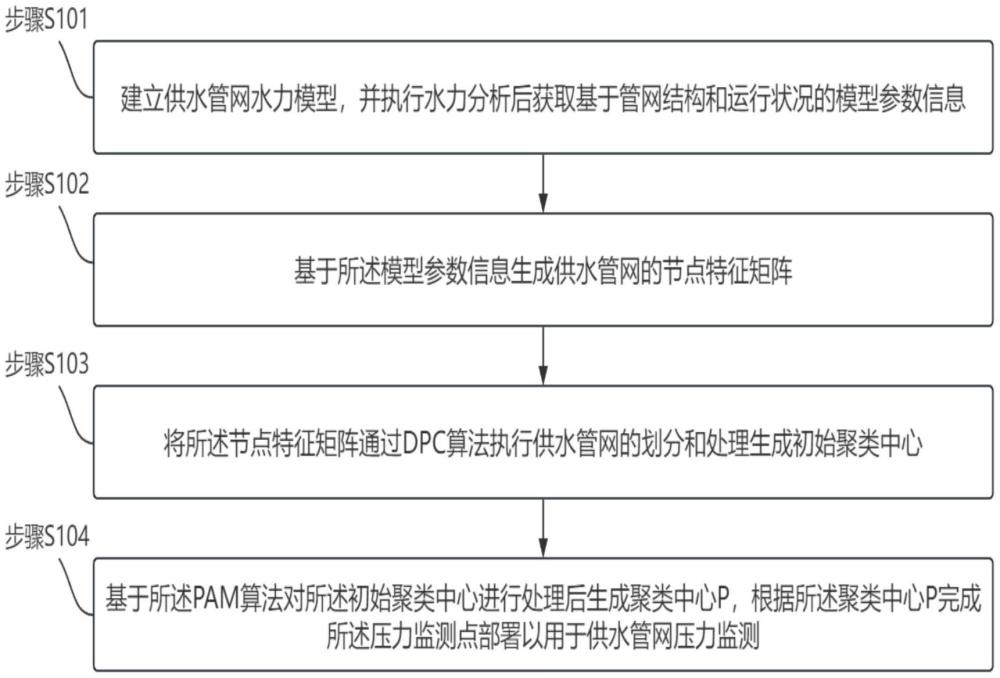
2、第一方面，本发明提出了一种基于密度峰值聚类改进围绕中心点划分算法的供水管网压力监测点布置方法，所述方法通过密度峰值聚类dpc算法改进围绕中心点划分pam算法进行供水管网压力监测点布置以用于供水管网压力监测，所述方法包括：

3、建立供水管网水力模型，并执行水力分析后获取基于管网结构和运行状况的模型参数信息；

4、基于所述模型参数信息生成供水管网的节点特征矩阵；

5、将所述节点特征矩阵通过dpc算法执行供水管网的划分和处理生成初始聚类中心c′；

6、基于所述pam算法对所述初始聚类中心c′进行处理后生成聚类中心p，根据所述聚类中心p完成所述供水管网压力监测点布置以用于供水管网压力监测。

7、进一步的，建立供水管网水力模型，并执行水力分析后获取基于管网结构和运行状况的模型参数信息的步骤具体包括：

8、根据实际供水管网的拓扑关系和管件运行参数建立供水管网水力模型，在所述供水管网水力模型中设定n个节点和m条管段；

9、基于所述供水管网水力模型执行水力分析，生成基于管网结构和运行状况的模型参数信息，所述模型参数信息包括各节点的位置坐标需水量q＝[q1,q2,...,qi]和压力值h＝[h1,h2,...,hi]，其中，i＝1,2,...,n。

10、进一步的，基于所述模型参数信息生成供水管网的节点特征矩阵的步骤具体包括：

11、在供水管网中通过逐个节点增加需水量来模拟泄漏，在第j个节点处设置喷射系数α与泄漏流量指数β，利用公式计算出该节点泄漏流量值qj，并执行水力分析，获取供水管网模拟各节点泄漏工况下管网所有节点的压力值h′：

12、

13、其中，hji表示当第j个节点发生泄漏时第i个节点的压力值，j＝1,2,...,n；

14、根据所述压力值h和压力值h′计算出节点j对节点i的影响系数x(i,j)并构建影响系数矩阵x：

15、

16、式中：hi、hj为供水管网无泄漏工况下节点i和节点j的压力值；hji、hjj为供水管网在节点j在泄漏工况下节点i的压力值；

17、

18、对所述影响系数矩阵x进行处理后得到矩阵x″和矩阵x″(i,j)：

19、

20、式中：x′jmax为x′第j列的最大值，x′jmin为x′第j列的最小值，的最小值，表示影响系数矩阵x的各列元素平均值，sj表示影响系数矩阵x的各列元素标准差；

21、基于所述矩阵x″(i,j)计算供水管网的节点j与供水管网n个节点中除节点j之外其他节点之间的平均欧式距离差矩阵r：

22、

23、通过以下公式计算节点j与供水管网n个节点中除节点j之外其他节点之间平均欧氏距离差的均值：

24、

25、将平均欧氏距离差的均值定义为供水管网n个节点的泄漏点灵敏度，构建供水管网各节点的泄漏点灵敏度矩阵

26、根据各节点的位置坐标与泄漏点灵敏度矩阵构成节点特征矩阵

27、进一步的，将所述节点特征矩阵通过dpc算法执行供水管网的划分和处理生成初始聚类中心c′的步骤具体包括：

28、将节点特征矩阵w定义为样本点集合：

29、w＝{y1,y2,…,yn}t

30、其中：

31、

32、输入数据集w＝{y1,y2,…,yn}t，设定簇的数量为t；

33、计算样本点yi和yj之间的欧式距离，公式如下；

34、

35、式中：表示样本点yi的第k个元素值；表示样本点yj的第k个元素值，k为数据集w的维数；

36、将样本点yi和yj之间的欧式距离矩阵定义为以下形式：

37、d＝{d1,d2,…,dn}t

38、其中：

39、d1＝{d11 d12…d1n}

40、d2＝{d21 d22…d2n}

41、

42、dn＝{dn1 dn2…dnn}

43、同时定义截断距离为dc，dc选取所有样本点yi为总数n的0.3％，公式如下：

44、

45、式中：表示向上取整操作符；

46、定义样本点yi的局部密度ρ＝{ρ1,ρ2,…,ρn}，计算公式如下：

47、

48、式中：dij为样本点yi和样本点yj之间的欧式距离；

49、计算样本点yi与yj之间的相对距离δ＝{δ1,δ2,…,δn}，计算公式如下：

50、

51、当样本点yj的局部密度ρj大于样本点yi的局部密度ρi时，δi选取欧式距离矩阵di中的最小值；当样本点yj的局部密度ρj小于等于样本点yi的局部密度ρi时，δi选取欧式距离矩阵di中的最大值。

52、将所求得样本点yi的局部密度ρi和相对距离δi相乘，再由大到小排序得到b＝{b1,b2,…,bn}，数组b所对应样本点为c＝{c1,c2,…,cn}，选取前t个样本点作为初始聚类中心，表示如下：c′＝{c1,c2,…,ct}，其中i＝1,2,...,n，j＝1,2,...,n，t＝1,2,...,t。

53、进一步的，基于所述pam算法对所述初始聚类中心c′进行处理后生成聚类中心p，根据所述聚类中心p完成所述供水管网压力监测点布置以用于供水管网压力监测的步骤具体包括：

54、根据初始聚类中心为c′＝{c1,c2,…,ct}，定义中心点以外的n-t个数据对象记为

55、利用以下公式计算到初始聚类中心c′＝{c1,c2,…,ct}的距离矩阵：

56、

57、并将距离矩阵定义为以下形式：

58、d′＝{d1′,d2′,…,d′n}

59、其中：

60、d1′＝{d1′1d2′1…d′n-t,1}t

61、d2′＝{d1′2d2′2…d′n-t,2}t

62、

63、d′n＝{d1′t d2′t…d′n-t,t}t

64、分别选取矩阵di′中的最小值，并将该值定义为n-t个数据对象中每一个数据对象与初始聚类中心点的最短距离，与每一个数据对象距离最短的点即为所对应的中心点，并将中的每一个数据对象分配到最近的中心点所处在的簇类中；

65、采用绝对误差函数为准则函数，计算误差平方和，公式如下：

66、

67、式中：e表示所有数据对象的绝对误差总和，ct为初始聚类中心c′＝{c1,c2,…,ct}中的一个中心点；

68、选取非簇中心的点代替中心点ct，计算替换中心点后新旧聚类的改变量，公式如下：

69、s＝e1-e2

70、式中：s表示绝对误差的改变量，e1表示未替换前数据集中所有代表点与其同簇中中心点之间的绝对误差之和；e2表示替换中心点后数据集中所有代表点与其同簇中中心点之间的绝对误差之和；

71、当s<0时，非簇中心的点当前隶属于中心点ci，如果将中心点ci替换为ch作为中心点，并且最接近ch，且i≠h，则被重新分配给ch；当s>0时，非簇中心的点当前隶属于中心点ci，如果将中心点ci替换为ch作为中心点，最接近ci，不被重新划分；

72、通过迭代计算直至数据对象的隶属不再发生变更结束聚类过程，确定输出t个簇生成聚类中心p，用p＝{p1,p2,…,pt}表示，其中，t＝1,2,...,t。

73、进一步的，根据所述聚类中心p完成所述供水管网压力监测点布置以用于供水管网压力监测的步骤具体包括：

74、根据所述聚类中心p＝{p1,p2,…,pt}，中心点的位置坐标其中，中心点的位置坐标为供水管网中压力传感器布置的位置坐标，聚类中心点的数量t即为压力传感器所需的数量，从而根据确定供水管网监测区域压力监测点的位置和数量完成所述供水管网压力监测点布置以用于供水管网压力监测。

75、与现有技术相比，本发明具有以下有益效果：

76、通过结合供水管网拓扑结构信息和运行状况信息构造出更全面反映供水管网当前状态的节点特征矩阵，包含节点空间属性和节点漏损灵敏度的节点特征矩阵解决了其他方法不考虑空间特征的问题，在更贴近真实供水管网特性的同时提高了后续压力监测点布置的可靠性。

77、本发明聚类阶段的重点是利用将dpc算法与pam算法相结合，目的是避免选出的初始聚类中心过于相近而导致聚类结果的不稳定，同时也避免了在同一簇中选择多个初始聚类中心而忽略数据对象较少的簇；pam算法作为一种典型的基于划分方式的无监督聚类算法，可以通过多次迭代对样本点进行聚类，其有着聚类思想简单、聚类过程可行性高，聚类时间复杂度接近线性等优点，同时对大规模数据挖掘也表现出良好的支持，被广泛应用于诸多领域。但pam算法的输入是随机选取的包含n个对象的数据，采用簇均值最近的数据点作为初始聚类中心的计算方法，在计算聚类中心的时候，由于数据集孤立噪声点的存在，使得计算出来的初始聚类中心可能会偏离真正的聚类中心，这就使得聚类结果不准确。基于dpc算法可以避免pam算法中选出的初始聚类中心过于相近而导致聚类结果的不稳定，同时也避免了在同一簇中选择多个初始聚类中心而忽略数据对象较少的簇，进而确认当前聚类中心数目下的最优压力监测点布置方案。