一种离网型零碳园区的风光电热冷气氢优化调度方法

本发明属于新能源，尤其涉及一种离网型零碳园区的风光电热冷气氢优化调度方法。

背景技术：

1、综合能源系统(ies)通常包括电、热、冷、气和氢等多种类型的能源，通过电转氢、氢转气、电制冷制热、热转冷等能源转换设备，可以实现异质能源之间的相互耦合及转换利用，在满足能源用户侧多元负荷需求的情况下，制定合理高效的协同运行调度策略，对保证系统可靠稳定运行和提高系统经济性与低碳环保性具有重要意义。

2、目前关于系统协同运行和优化调度的研究，传统的方法是使用数学中的优化类方法，例如：非线性规划、二阶锥规划和混合整数规划等，然后利用yalmip、cplex、gurobi和mosek等成熟的商业求解器直接进行求解，但是随着问题规模的扩大将会面临计算时间急剧上升的情况，甚至在大规模问题下变得难以求解。

3、当前也有很多研究人员将粒子群优化算法(pso)、遗传算法(ga)和模拟退火算法(sa)等智能优化算法应用于综合能源系统多目标问题的求解上，这些算法的求解结果的好坏和其中的静态参数是否合理的设置有很大关系，非常依赖使用者的经验，同时在求解多目标优化问题的时候容易陷入局部最优解，这导致获得的调度结果不能保证系统高效、稳定和经济地运行。

4、随着多种能源转换设备被引入到综合能源系统，以及后端需求的多元化，系统的结构和耦合关系都变得更加复杂。对于这种复杂的、非线性的、高维度的系统，深度强化学习(drl)中的智能体通过在环境中采取一系列行动，环境根据智能体的行动反馈奖励信号，不断学习得到最优调度策略。深度q网络算法(dqn)只能处理离散动作空间，对于复杂的综合能源系统易出现维度爆炸的问题；深度确定性策略梯度算法(ddpg)虽然能处理连续动作空间，但也存在着估计值过高、策略网络更新不稳定和探索不充分的问题；双延迟深度确定性策略梯度算法(td3)在处理连续动作空间的问题上表现出了较好的性能，但是其对超参数的选择非常敏感，加上更加复杂的模型，这导致会耗费巨大的计算机资源。

技术实现思路

1、针对现有技术中的不足，本发明提供一种离网型零碳园区的风光电热冷气氢优化调度方法，以期望在源荷出现波动，且不能从外部买电和买气的情况下，仍尽可能地满足负荷侧的需求，最终实现系统稳定和经济地运行。

2、本发明的一种离网型零碳园区的风光电热冷气氢优化调度方法，包括以下步骤：

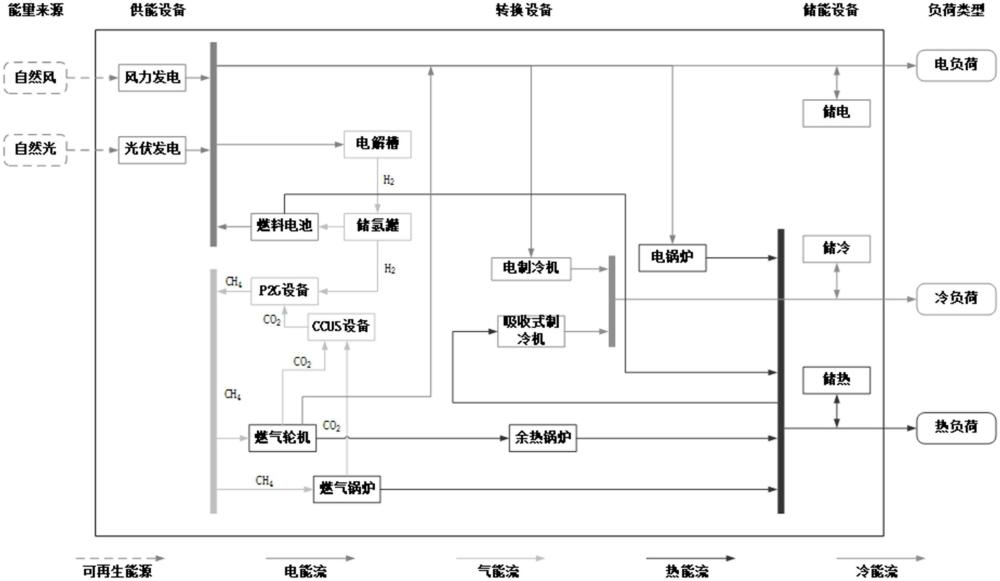
3、步骤1：建立离网型零碳园区系统模型，该系统包括供能设备、能源转换设备、能量储存设备，能量来源是可再生能源风能和光能，负荷类型包括电负荷、热负荷、冷负荷。

4、供能设备包括风力发电机组wt和光伏板发电机组pv；能源转换设备包括冷热电三联供系统cchp、燃气锅炉gb、电解槽el、燃料电池hfc、甲烷反应器mr、碳捕集设备ccus、电制冷机ec和电锅炉eb；能量储存设备包括蓄电池bat、储氢罐hst、蓄热装置hes和蓄冷装置ces。

5、其中的冷热电三联供系统具体由燃气轮机gt、余热回收装置whr、吸收式制冷机ac、余热锅炉whb组成。

6、步骤1.1：根据上述离网型零碳园区系统模型，构建数学模型以及运行约束条件。

7、(1)风力发电机组wt数学模型以及运行约束条件。

8、

9、0≤pwt(t)≤pwt,max(t)       (2)

10、式中，pwt,max(t)为t时刻风力发电机组所能输出的最大发电功率；nwt为风机数量；pwt,rated为单个风机的额定功率；νw(t)为在风力电机高度处t时刻的风电机组运行风速；νrated为风力机组的额定风速；vin为风力机组的切入风速；vout为风力机组切出风速；pwt(t)为t时刻风力发电机组实际输出的发电功率。

11、(2)光伏发电机组pv数学模型以及运行约束条件。

12、

13、式中，ppv,max(t)为光伏发电机组在t时刻所能输出的最大发电功率；fpv为光伏板的衰减系数；ppv,rated为单个光伏板的额定功率；sa(t)为t时刻实际的光照强度；sstc为标准环境下的光照强度；kpv为功率温度系数；tpv(t)为t时刻光伏板表面的实际温度；tstc标准环境下光伏板表面的温度。

14、光伏板表面的实际温度tpv(t)的计算公式为：

15、

16、0≤ppv(t)≤ppv,max(t)       (5)

17、式中，tamb为环境温度；noct表示工况标称下的光伏组件工作温度，由光伏制作商提供；ppv(t)为t时刻实际的光伏发电机组输出的发电功率。

18、(3)冷热电三联供系统cchp数学模型以及运行约束条件。

19、

20、式中，pg,gt(t)为t时刻输入到gt的天然气功率，即gt的运行功率；pgt,e(t)和pgt,h(t)分别为t时刻的gt输出的电功率和热功率；ηgt为gt的能量转换效率；和分别表示gt的可调热电比上限和下限；和为输入到gt机组的天然气功率上限和下限；和为gt机组爬升功率的上下限。

21、

22、式中，k为1kwh电能所对应的能量即3.6×106j；为天然气热值，表示单位体积天然气燃烧所释放的热量；mg,gt(t)为t时gt机组所消耗的天然气质量；为单位质量天然气完全燃烧产生co2的质量；为t时刻gt机组所产生的二氧化碳的质量。

23、

24、式中，ph,ac(t)为t时刻输入到ac的热功率，及ac的运行功率；pac,c(t)为t时刻ac输出的冷功率；为ac热转冷的转换效率；和为ac运行功率的上限和下限；和为ac机组爬升功率的上下限。

25、

26、式中，ph,whb(t)为t时刻输入到whb的热功率，及whb的运行功率；pwhb,h(t)为t时刻whb输出的热功率；为whb热转热的转换效率；和为whb运行功率的上限和下限；和为whb机组爬升功率的上下限。

27、(4)燃气锅炉gb数学模型以及运行约束条件。

28、

29、式中，pg,gb(t)为t时刻输入到gb的天然气功率，及gb的运行功率；pgb,h(t)为t时刻gb输出的热功率；为gb天然气转热的转换效率；和为gb运行功率的上限和下限；和为gb机组爬升功率的上下限。

30、

31、式中，k为1kwh电能所对应的能量即3.6×106j；为天然气热值，表示单位体积天然气燃烧所释放的热量；mg,gb(t)为t时刻gb机组所消耗的天然气体积；为单位质量天然气完全燃烧产生co2的质量；为t时刻gb机组所产生的二氧化碳的质量。

32、(5)电解槽el数学模型以及运行约束条件。

33、

34、式中，pe,el(t)为t时刻输入到el的天然气功率，及el的运行功率；pel,h(t)为t时刻el输出的氢功率；为el电转氢的转换效率；和为el运行功率的上限和下限；和为el机组爬升功率的上下限。

35、(6)燃料电池hfc数学模型以及运行约束条件。

36、

37、式中，ph,hfc(t)为t时刻输入到hfc的氢气功率，即hfc的运行功率；phfc,e(t)和phfc,h(t)分别为hfc输出的电功率和热功率；ηhfc为hfc的能量转换效率；和分别表示hfc的可调热电比上限和下限；和为输入到hfc机组的氢气功率上限和下限；和为hfc机组爬升功率的上下限。

38、(7)甲烷反应器mr数学模型以及运行约束条件。

39、

40、式中，ph,mr(t)为t时刻输入到mr的氢功率，及mr的运行功率；pmr,g(t)为t时刻mr输出的天然气功率；为mr生产氢转天然气的转换效率；和为输入到mr机组的氢气功率上限和下限；和为mr机组爬升功率的上下限。

41、

42、式中，为t时刻mr生成的天然气的质量；为生成单位质量的天然气需要的二氧化碳的质量；为t时刻mr所消耗的二氧化碳的质量。

43、(8)碳捕集ccus数学模型以及运行约束条件。

44、

45、式中，ηccus为吸收单位质量的二氧化碳所需要消耗的电能；pe,ccus(t)为t时刻ccus所吸收的二氧化碳的质量。

46、(9)电制冷ec数学模型以及运行约束条件。

47、

48、式中，pe,ec(t)为t时刻输入到ec的电功率，及ec的运行功率；pec,c(t)为t时刻ec输出的冷功率；为ec电转冷的转换效率；和为ec运行功率的上限和下限；和为ec机组爬升功率的上下限。

49、(10)电锅炉eb数学模型以及运行约束条件。

50、

51、式中，pe,eb(t)为t时刻输入到eb的电功率，及eb的运行功率；peb,h(t)为t时刻ec输出的热功率；为ec电转冷的转换效率；和为eb运行功率的上限和下限；和为ec机组爬升功率的上下限。

52、(11)储能设备通用数学模型以及运行约束条件。

53、对电、热、冷三种储能装置的运行机理进行相同的处理，因此对储能装置进行了统一的建模，如下所示：

54、

55、式中，n为电、热、冷其中之一；和为t时刻储能装置充放能功率；和为二进制变量，表示储能设备在t时刻充能量，表示释放能量；soces,n(t)为t时刻储能设备最终的余量；和为充放能效率；t为最大的运行时长；为储能设备的最大容量；为储能设备的初始容量系数；为了减小过充过放对储能设备寿命的影响，设置了最低和最高容量系数

56、(12)电功率平衡约束条件。

57、

58、式中，peload(t)为t时刻电负荷需求。

59、(13)热功率平衡约束条件。

60、

61、式中，phload(t)为t时刻热负荷需求。

62、(14)冷功率平衡约束条件。

63、

64、(15)氢功率平衡约束。

65、

66、(16)天然气功率平衡约束。

67、pmr,g(t)＝pg,gt(t)+pg,gb(t)         (24)

68、步骤1.2：针对离网型零碳园区系统建立优化目标函数：

69、f＝min(copm)(25)

70、

71、式中，copm为各个设备的运维总成本；copm,i为第i个设备的单位运维成本；pi为第i个设备的运行功率。

72、步骤2：将离网型零碳园区系统优化调度强化学习框架描述为一个马尔科夫决策过程：

73、步骤2.1：建立状态空间：

74、st＝[vw(t),sa(t),peload(t),phload(t),pcload(t),soces,n(t),t](27)

75、步骤2.2：建立动作空间：

76、

77、步骤2.2：建立奖励函数：

78、rt＝-copm      (29)

79、步骤3：基于改进的柔性行动者-评论家算法求解模型。

80、具体是指将优势学习与迁移学习与sac算法结合。

81、sac算法的目标函数表达式如下：

82、

83、式中，(sq,aq)～pπ为策略π状态动作轨迹；α为超参数，决定熵对于奖励的影响程度；αh(π(·|st))为状态st时的熵，具体计算公式如下所示：

84、

85、上式表示策略π(·|st)对应概率分布的随机程度，策略越随机，熵越大。

86、sac算法也是使用的ac框架，但做出来改进，提出了软值函数，对状态价值函数和q值函数公式中加入了熵，如下所示：

87、

88、式中，tπ为策略π下的贝尔曼算子，γ为奖励的折扣因子，同时结合贝尔曼算子如下所示：

89、

90、式中，为第k次计算时的价值函数，软值函数通过公式(33)进行迭代，最终会收敛到固定策略π下的软q值函数。

91、为了避免出现策略差异过大导致训练失稳的情况，在策略更新中，将策略输出位高斯分布，再利用kl散来缩小新旧策略差距，公式如下所示：

92、

93、式中，dkl是kl散度；为旧策略πold下的值函数；π为策略集合；为旧策略下的分配函数，可对q值进行归一化。

94、sac的critic和actor神经网络参数更新分别如下：

95、

96、式中，θ、φ为q值网络和策略网络参数；和为更新后的函数，zθ(st)为分配函数。

97、在策略网络中也会输出动作熵，其中超参数α的更新对于熵至关重要，其更新式为：

98、

99、式中，h0为动作矩阵维数。

100、进一步的，在值函数的估计中，优势学习会通过降低非最优动作的q值估计，提高智能体对最优动作的被选概率来加快算法在训练时的收敛速度；其中，优势学习的状态值函数公式如下：

101、

102、式中，a*(s,a)为优势函数，定义如下所示：

103、a*(s,a)＝v*(s)-α[v*(s)-q*(s,a)]        (40)

104、式中，α[v*(s)-q*(s,a)]为修正项，q*(s,a)的值为最优动作的q值时，修正项为零，否则为正。

105、将环境状态st输入策略网络中，从此网络中输出的动作at+1作为最优动作，再将at+1以及状态st输入到q值网络critic，其输出的值视为当前最优状态值q(st,at+1；θ-)，则修正项函数改写为：

106、f(st,at)＝α[q(st,at+1；θ-)-q(st,at；θ-)]           (41)

107、为防止当网络输出的q(st,at；θ-)大于q(st,at；θ-)时，f(st,at)的值小于零，这时减去f(st,at)时会增加q值导致出现过估计，因此增加限制：当f(st,at)＞0时，f(st,at)的值不变；f(st,at)＜0时，f(st,at)的值为0。

108、还需对神经网络的稳定性进行判断，因此采用网络损失函数的下降率作为是否启动优势学习判断依据；网络损失函数的下降率公式如下：

109、

110、式中，loss(t)为神经网络损失函数，k为下降倍率；若k小于启动优势学习所设置的阈值时，则不启动优势学习；反之则启动优势学习。

111、目标q值公式改为：

112、

113、在相同环境中处理不同任务时，采用知识迁移的策略，最大限度地利用已有的知识，从而提高深度强化学习的效率。

114、在实际操作中，用历史数据训练更新的神经网络权值对目标网络的神经网络权值进行初始化，以代替神经网络的随机权值初始化。

115、本发明是有益技术效果为：

116、本发明主要考虑的是偏远地区离网型的综合能源系统，针对可再生能源和负荷的波动性问题和低碳环保性问题，以包含电热冷气氢多种能源的综合能源系统为研究对象，通过引入cchp和hfc两套热电联产系统，充分利用多能互补优势，提高系统的经济性和环保性；采用基于改进的柔性行动者-评论家算法，有效避免了动作空间的“维数灾”问题，并进一步减少训练时间加快算法迭代速度，实现综合能源系统调度的灵活高效。