一种承插式管材的插口和承口厚度的设计方法与流程

本发明属于管材设计，具体为一种承插式管材的插口和承口厚度的设计方法。

背景技术：

1、生活和生产用给排水系统的水管大多为承插式管材，其一端为承口、另一端为插口，安装时，一根管材的插口插入另一管材的承口，并通过密封件进行密封，如此实现管网中各管材的连接。如图5和6中，m为插口，f为承口。对于正常使用的给水管，会承受较大的内部供水压力，该内部压力为正压，因此管材必须满足规定的强度要求。现有一些标准（团体标准和国家标准）中规定了不同压力等级和不同公称直径下的公称壁厚，符合标准的管材在对应的压力等级范围内均能满足强度要求。因此，现有管材生产企业生产的管材一般都符合相应标准规定。

2、但是，当管网出现故障，例如，管网中有管材发生爆管时，管网中的水会从爆管处喷出，管网中的压力会迅速下降，甚至形成负压。另外，管材还会受到一些外部压力，例如埋在土体中的管材会受到其上部土体的重力。在上述外部压力和内部负压作用下，管材会产生径向上的变形，若插口变形量过大，插口会和与其连接的承口分离，导致承口和插口的连接处发生泄漏，使水管内部受到污染。因此，需要保证管材的插口在上述情况下的变形不超出一定范围。为此，对于插口，要获得满足变形要求的最小插口厚度，若选用的管材的插口厚度小于满足变形要求的最小插口厚度，则需要采取措施，使其满足变形要求，例如，在管材二次加工或安装时，在插口套接环形加强圈，以增强抵抗变形的能力。而对于承口f，现有标准没有给出其壁厚要求，但一般都需要保证其厚度足够以满足强度要求，最好使承口f各处的厚度在满足使用强度的同时厚度最小或接近最小。

技术实现思路

1、针对现有技术存在的上述问题，本发明的目的是提供一种承插式管材的插口和承口厚度的设计方法，可通过理论分析和计算获得不同管径的承插式管材满足变形要求的插口最小或接近最小的厚度以及满足强度要求的承口最小或接近最小厚度，节约了材料，降低了管材的生产、制造和运输成本，设计最小壁厚的方法为理论计算，成本低、效率高，为实验和管材设计提供了有力支撑，为二次加工和安装提供参考；若管材的插口或承口的厚度小于计算得到的最小厚度，则可通过在插口或承口安装加强圈提高插口或承口厚度来使插口满足变形要求、承口满足强度要求，如此安装的管材和管网系统使用更可靠，大大降低了管材发生爆管时相邻管材的插口和承口发生变形分离导致的漏水和供水被污染的情况，以及承口发生裂开的情况。

2、为了实现上述目的，本发明所采用的技术方案是：

3、一种承插式管材的插口和承口厚度的设计方法，插口厚度的设计方法包括如下步骤：

4、步骤a1：根据圆环的挠曲线微分方程和力矩平衡方程获得圆环的径向变形的微分方程和微分方程的通解；

5、步骤a2：根据步骤a1得到的微分方程的通解计算并获得所述圆环径向变形最大量的计算公式；

6、步骤a3：根据步骤a2获得的径向变形最大量的计算公式求得基管的满足变形要求的插口最小厚度；

7、承口厚度的设计方法包括如下步骤：

8、步骤b1：选取承口内壁上应力易集中的多处，选取原则为：若这几处的壁厚满足应力强度要求，则按照外壁设计要求设计的承口每一处壁厚都满足强度要求；

9、步骤b2：确定步骤b1中各选取处的最小壁厚，得到各选取处的外壁，确定原则为：当承口的材质和管身的材质相同时，各选取处的应力不大于管身内壁应力；当承口的材质和管身的材质不相同时，各选取处的应力与承口材质的屈服强度的比值不大于管身内壁应力与管身材质的屈服强度的比值。

10、作为上述技术方案的进一步改进：

11、步骤a2包括如下步骤：

12、步骤a21：假设所述圆环受到至少两个相对圆心对称的径向集中力，基于所述假设，计算微分方程通解中的常数项，获得微分方程第一形式；

13、步骤a22：基于步骤a21获得的微分方程第一形式，假设所述圆环只受到两个相对圆心对称的径向集中力，则微分方程第一形式变换为微分方程第二形式；

14、步骤a23：通过引入系数将所述圆环受到的内部负压引入微分方程第二形式，获得微分方程第三形式；

15、步骤a24：根据步骤a23得到的微分方程第三形式获得带系数的所述圆环直径最大变化量的计算公式。

16、步骤a3包括如下步骤：

17、步骤a31：根据已有剪切载荷公式计算一参考管材的参数，所述参考管材的材质、外径分别和基管的材质、外径相同；

18、步骤a32：根据步骤a31计算得到的参数通过仿真模拟获得所述参考管材插口最大变形量；

19、步骤a33：将步骤a32获得的插口最大变形量代入步骤a2的计算公式，得到所述计算公式中的系数值，从而得到已知系数的圆环径向变形最大量的计算公式；

20、步骤a34：根据许用变形规定和步骤a33得到的公式计算得到基管的满足变形要求的插口最小厚度。

21、步骤a1中，得到的径向变形量 u的微分方程为：

22、；

23、其通解为：；

24、其中， r为所述圆环的外圆半径和内圆半径的平均值； e是管材的弹性模量，pa；i是圆管截面的惯性矩，m4； m是局部区域某段圆环承受的弯矩，单位n*m；建立二维坐标系，是变形量为 u处的点和坐标系原点的连线与二维坐标系中x轴正方向之间的夹角，；a1、a2、a3、b2、b3为常数。

25、步骤a2中，假设所述圆环受到至少两个相对圆心对称的径向集中力p，且相邻两个径向集中力p之间的夹角为，所述圆环满足以下三个边界条件：

26、（1）在处，由于对称性，处截面的转角为0，即满足以下公式：；

27、（2）由于对称性，每一等分段内的圆弧的总的切向位移为0；即有：；

28、（3）在a点临近切开，去除a点及作用的力p，由对称性及平衡条件可知，圆环切口处截面上的剪力，即有：；

29、联立以上三个公式和微分方程的通解，得到微分方程第一形式：

30、；

31、假设所述圆环只受到两个相对圆心对称的径向集中力p，则：，得到微分方程第二形式：

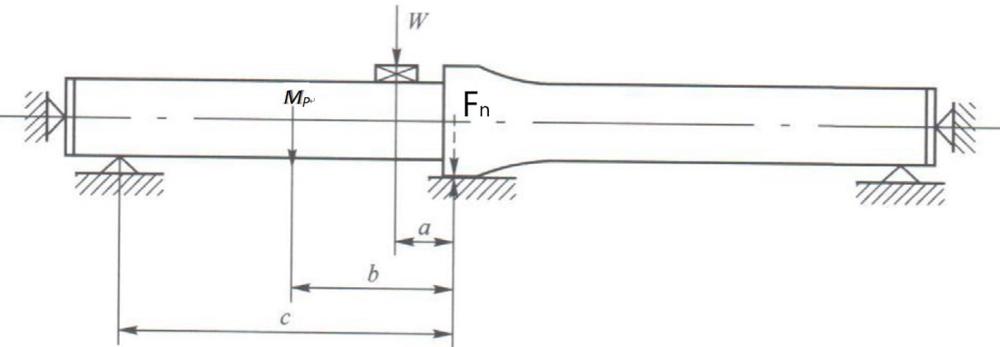
32、；

33、引入系数m，得到微分方程第三形式：

34、；

35、作用力p的作用点处为最大变形量处，圆环直径变化量为：

36、，其中，i=s3/12，s为管身厚度。

37、步骤a31中采用的剪切载荷公式为：

38、，

39、其中： w为剪切载荷，单位为牛顿（n）； f n为作用于接口的剪切力，单位为牛顿（n）； m p为试验组件管材重量和管材内物体重量，单位为千克（kg）； a为剪切载荷施力点与已插入承口的插口端面的距离，单位为毫米（mm）； b为插口端管材重心与已插入承口的插口端面的距离，单位为毫米（mm）； c为垫块支撑点与已插入承口的插口端面的距离，单位为毫米（mm）。

40、对于同一基管，沿着从承口到插口的方向，承口的内壁包括依次排列的第一阶梯、第二阶梯、第三阶梯、第四阶梯、第五阶梯，管身的内壁一端为第六阶梯，对应的内径分别为：d2、d1、（d3-2f0）、d3、d4、（d0-2s），且（d0-2s）＜d2＜d4＜（d3-2f0）＜d3＜d1，第一阶梯、第二阶梯、第三阶梯、第四阶梯、第五阶梯的长度分别为：t3、t4、t5、（t2-t4-t5）、（t1-t2-t3），第四阶梯和第五阶梯连接处的倒角为第一倒角，第五阶梯和第六阶梯连接处的倒角为第二倒角，第二阶梯和第三阶梯连接处的倒角为第三倒角，第一阶梯和第二阶梯连接处的倒角为第四倒角、第三阶梯和第四阶梯连接处的倒角为第五倒角，d0是基管外径。

41、步骤b1中，选取的承口内壁上应力易集中的几处分别为第一倒角处、第二倒角处和第三倒角处。

42、步骤b2中，通过应力计算公式计算得到步骤b1中各选取处的最小壁厚，把承口视作包括至少两个同轴连接的内壁为圆锥面的压力容器加上至少一个安装在压力容器内壁上的环形加强圈，，，其中，为管身的环向应力，为选取处的环向应力，d0是基管外径，d是选取处直径，p是基管内流体的压力，s为基管厚度，s0为选取处的壁厚，α为选取处所在圆锥的半锥角。

43、当承口的材质和管身的材质相同时，所述应力计算公式为：。

44、当承口的材质和管身的材质不相同时，所述应力计算公式为：，其中，q0为管身材料的屈服强度，q1为承口所用材料的屈服强度。

45、本发明的有益效果是：可通过理论分析和计算获得不同管径的承插式管材满足变形要求的插口最小或接近最小的厚度以及满足强度要求的承口最小或接近最小厚度，节约了材料，降低了管材的生产、制造和运输成本，设计最小壁厚的方法为理论计算，成本低、效率高，为实验和管材设计提供了有力支撑，为二次加工和安装提供参考；若管材的插口或承口的厚度小于计算得到的最小厚度，则可通过在插口或承口安装加强圈提高插口或承口厚度来使插口满足变形要求、承口满足强度要求，如此安装的管材和管网系统使用更可靠，大大降低了管材发生爆管时由于插口变形过度导致相邻管材的插口和承口分离导致的漏水和供水被污染的情况，以及承口发生裂开的情况。