一种考虑测量条件下针对复杂结构装备的可靠性分析方法

本发明属于可靠性分析领域，涉及一种考虑测量条件下针对复杂结构装备的可靠性分析方法。

背景技术：

1、结构可靠性估计在工程领域，尤其是建筑、航空航天、桥梁、机械和其他需要承受物理应力的结构设计中，扮演着至关重要的角色。结构可靠性不仅涉及结构的安全性，还包括适用性和耐久性，它通过概率指标——结构可靠度来定量分析。在设计、建造和使用过程中，由于存在各种不确定性，使得结构可靠性的评估变得复杂且必要。

2、现有常用的结构可靠性计算方法有蒙特卡洛法，代理模型法，一次二阶矩法等。中国发明专利《一种考虑滚动接触疲劳损伤和磨损耦合作用的轴承时变可靠性分析方法》（专利号：202411171631.x），该发明提出一种新颖的轴承可靠性分析物理模型，建立了轴承的rcf损伤与磨损耦合效应，更合理、准确地评估可靠性的同时显著提高了计算效率。中国发明专利《证据不确定性下涡轮机匣可靠性分析的代理模型方法》（专利号：202311359650.0），该发明可以稳健快速地计算证据不确定性下涡轮机匣结构的失效概率界限，从而合理评估涡轮机匣的可靠性水平。然而，这些发明都研究的是不含测量条件下结构的可靠性分析方法。在许多工程问题中，如建筑健康监测，工程师通常会在结构上布置测量点来测量结构响应。这种含测量条件情况下结构的可靠性分析方法尚未被研究。在用随机参数量化结构的随机动力响应时，如果可以考虑测量数据条件，很明显可以进一步细化随机响应的不确定性量化，为结构安全性和可靠性分析提供更可靠的依据。同时，在实际工程问题中，人为操作和仪器误差引起的测量误差也具有随机性。

3、因此，在具有随机误差的测量条件下，如何准确有效地评估复杂结构装备的可靠性是一个极其重要的问题。

技术实现思路

1、针对现有技术存在的问题，本发明提供一种考虑测量条件下针对复杂结构装备的可靠性分析方法。本发明基于概率守恒定律，推导出了含测量条件下的力学概率指标的条件概率密度函数的精确表达式。与无条件情况下的分析相比，本发明所提出的在测量条件下的复杂结构装备可靠性分析方法，能够得出更为精确的结果，从而为结构的安全性和可靠性评估提供了更加坚实的依据。本发明填补了存在测量数据时，结构装备可靠性分析研究的空白。

2、为了达到上述目的，本发明采用的技术方案为：

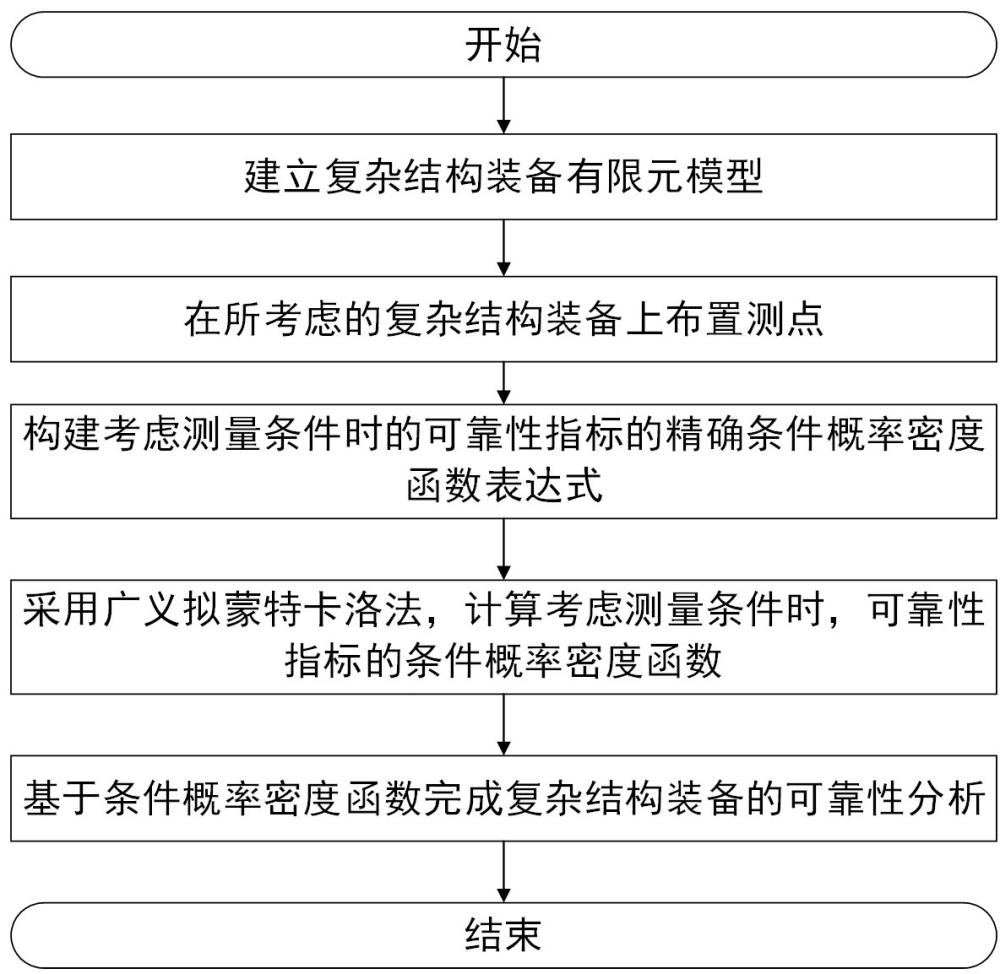
3、一种考虑测量条件下针对复杂结构装备的可靠性分析方法，所述可靠性分析方法首先，建立复杂结构装备有限元模型，求得结构响应。其次，在所考虑的复杂结构上布置测点。然后，构建考虑测量条件时的可靠性指标的精确条件概率密度函数表达式。再使用广义拟蒙特卡罗法求解考虑测量条件时的可靠性指标的条件概率密度函数。最后，基于条件概率密度函数完成结构的可靠性分析。包括以下步骤：

4、第一步，建立复杂结构装备有限元模型，求得结构响应；具体的：

5、步骤1.1，在三维建模软件中导入已有的复杂结构装备模型，或根据工程图对复杂结构装备的三维模型进行建模，得到复杂结构装备有限元模型。

6、步骤1.2，基于步骤1.1建立的复杂结构装备有限元模型，根据实际问题确定复杂结构装备相应的材料属性、约束和载荷。

7、步骤1.3，根据实际需求，确定复杂结构装备中存在的不确定性随机变量，以及变量的概率密度函数。当不确定性变量存在多个时，为一个向量，每个分量对应不同的不确定性变量。

8、基于以上步骤，得到了复杂结构装备有限元模型，载荷约束和不确定性变量的分布。当给定值时，可以代入复杂结构装备有限元模型，计算得到复杂结构装备在时刻的响应。

9、第二步，在所考虑的复杂结构装备上布置测点，具体的：

10、步骤2.1，在复杂结构装备的关键节点处布置测点，进行测量，得到实际测量值，测量值随时间累积。关键节点位置可以基于经验或历史数据判断确定。

11、步骤2.2，测量过程中不可避免总是存在随机的测量误差，根据所选择的测量仪器的量程，确定测试噪声。测量噪声设为平稳高斯过程，用表示，其概率密度为。

12、步骤2.3，已知实测值和测量噪声后，得到测量方程：

13、（1）

14、其中，是复杂结构装备的测量函数，它描述了不含测量噪声的条件下，测量值和结构响应之间的关系；表示的简化写法；表示时刻值。

15、第三步，构建考虑测量条件时的可靠性指标的精确条件概率密度函数表达式，具体的：

16、步骤3.1，定义需要分析的力学可靠性指标，该力学可靠性指标是响应的函数，因此也就是不确定性随机变量的函数。因此，表示为。

17、步骤3.2，求解已知测量数据条件时，的条件概率密度函数，表示为：

18、（2）

19、其中，为的联合概率密度；为实测值的概率密度。

20、根据概率守恒定律，复杂结构装备有限元模型与量测条件构成的系统的联合概率密度写为：

21、（3）

22、其中，为狄拉克函数，在除零点之外的点函数值都等于零，而在整个定义域上的积分等于1；表示所有时间步测量噪声的联合概率密度函数，的定义详见步骤1.3，表示当所有时间步测量噪声恰好为时，对应的联合概率密度函数的数值；

23、通过对随机变量和测量噪声的积分得到边缘概率密度，如公式（4）所示：

24、（4）

25、再对积分得：

26、（5）

27、此时，将和作为分子和分母，代入概率密度函数表达式（2）中，求得已知测量数据条件时，的条件概率密度函数。

28、第四步，采用广义拟蒙特卡罗法，计算考虑测量条件时，可靠性指标的条件概率密度函数，具体的：

29、步骤4.1，使用拟蒙特卡罗法求解这一高维积分。

30、首先，使用广义低偏差采样方法，对所考虑复杂结构装备中的随机变量进行采样。采样遵循的概率分布，采得个样本点，并求得其对应的点集权重。

31、将获得的个样本点代入步骤1.1中的复杂结构装备有限元模型中，计算得到对应的，然后用公式（6）所示的广义拟蒙特卡罗计算格式计算实测值的概率密度函数：

32、（6）

33、步骤4.2，是一个包含非光滑狄拉克函数的高维积分，无法直接计算。需要首先使用高斯函数对狄拉克函数进行近似，再使用广义拟蒙特卡罗方法求解，此时公式（4）改写为：

34、（7）

35、其中，当使用高斯函数近似时，表示光滑因子。

36、步骤4.3，将求得的和代入公式（2），此时求解完毕。

37、第五步，基于条件概率密度函数完成复杂结构装备的可靠性分析，具体如下：

38、步骤5.1，根据实际问题，确定所考虑的复杂结构装备正常使用时的的允许阈值。

39、步骤5.2，此时复杂结构装备的可靠概率表示为，使用，对其进行数值积分求解得到复杂结构装备的可靠概率，完成复杂结构装备的可靠性分析。

40、与现有技术相比，本发明具有以下有益效果：

41、（1）本发明基于概率守恒定律，结合广义拟蒙特卡洛法推导并求解出了含测量条件下的力学概率指标的条件概率密度函数，完成了复杂结构装备的可靠性分析，首次解决了存在测量条件时复杂结构装备的可靠性问题，填补了存在测量数据时结构装备可靠性分析研究的空白。

42、（2）相比无条件情况，本发明给出的存在测量条件时复杂结构装备的可靠性分析方法得到的结果更加精确，为结构安全性和可靠性分析提供更可靠的依据。

43、（3）本发明采用广义拟蒙特卡罗法计算高维积分问题，相比传统的蒙特卡罗法和拟蒙特卡罗法，需要的样本点数量更少，精度更高，计算效率更好。