基于桥梁动应变识别车队车辆数的方法与流程

本发明涉及桥梁试验检测、健康监控及超载车治理领域，特别是基于桥梁动应变识别车队车辆数的方法。
背景技术：
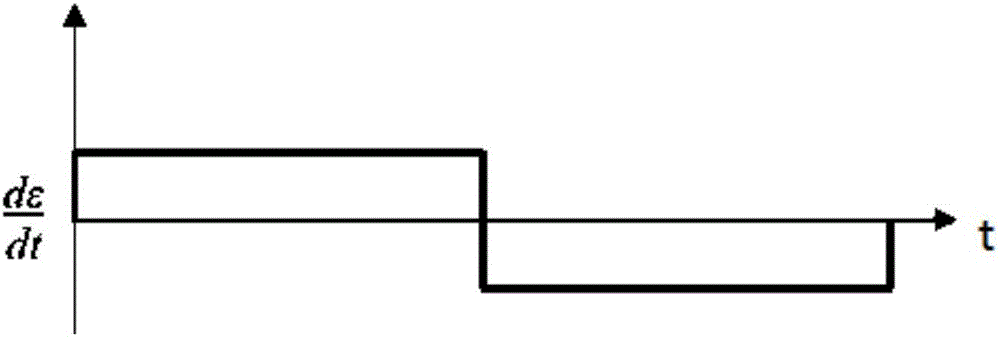
：近年来，我国陆续出现了多次重大桥梁事故。这些发生的事故与很多因素有关，但是缺乏有效的监测措施和必要的维修、养护措施是重要的原因之一。这些触目惊心的事故使得人们对现代桥梁的质量和寿命也逐渐关注起来。对桥梁结构进行试验检测、健康监测和交通运输治理超载车辆，已成为国内外学术界、工程界研究的热点。传统的桥梁检测在很大程度上依赖于管理者和技术人员的经验，往往对桥梁特别是大型桥梁的状况缺乏全面的把握和了解，信息得不到及时反馈。如果对桥梁的病害估计不足，就很可能失去养护的最佳时机，加快桥梁损坏的进程，缩短桥梁的服务寿命。如果对桥梁的病害估计过高，便会造成不必要的资金浪费，使得桥梁的承载能力不能充分发挥。目前，车辆超重行驶的现象频频出现，而桥梁的负载是有一定的限度，当这些超重的车辆通过桥梁，无疑会对桥梁产生一定的损害；而且随着时间的推移，桥梁的老化，其承载能力也在变化，因此监测通过桥梁车辆的重量，并进行数据统计，对于了解桥梁的健康状况意义重大。但是一般常规地磅测重设备价格昂贵，单车道最便宜的也需要10万元以上，且安装时需要破坏原路面结构；使用时常规称重地磅需要人为或借助摄像设备判别车辆及车轴数量；且常规地磅安装在桥梁主体结构以外的路面上，多车道桥梁采用常规地磅难以对桥上并排行驶车辆对桥梁的影响进行统计。即使用常规的称重地磅并不适用与桥梁上的车辆车轴数、车轴距或车轴重的测量，所以，社会上急需一种适用于测量在桥梁行驶的车辆总重量、车轴数、车轴距或车轴重的低成本方法或设备。中国专利201210249735.9公开基于桥梁动应变识别车辆重量的方法，包括以下步骤：在桥梁纵向对称截面上布置动应变测量装置；在安装好动应变测量装置的桥梁行车道上进行跑车实验，同时采集数据，并将数据传输至计算机；采用有限元仿真计算理论动应变，提取动应变结果形成的动应变时程曲线，并与实测值进行比较及相关分析，得出行车速度、动应变峰值及车辆重量的关系式T＝f(x,ε)或是曲线；根据各截面动应变达到峰值的时间差和截面距离采用软件自动计算行车速度，同截面各测点动应变峰值取平均，带入关系式T＝f(x,ε)或是曲线进行计算或比对求得通过该截面的车重。这里通过试验寻找行车速度、动应变峰值及车辆重量的关系式，存在工作量大、适应性不高的问题，特别是每个桥梁的结构特性均不相同，这样导致每次安装都需要对在使用中的桥梁需要进行封闭性试验、且试验次数多、安装效率低、安装使用成本高，其推广程度不高，无法应对中国目前桥梁的测量需求。中国专利201610114464.4公开了一种用于桥梁的车轴识别方法及系统，该方法包括步骤：沿桥梁纵长方向标记共包含4～6个截面的两个截面组，形成两座虚拟简支梁；采集测量两个截面组处的桥梁时程响应，根据时程响应计算得到两组隔离响应，将两组隔离响应分别构建两条响应时程曲线；对响应时程曲线上的局部峰值数量进行统计，得到车辆轴或者轴组的数量N。这里通过建立模拟方案，并由响应时程曲线来实现车轴数的判断，但需要安装多组传感器以形成相互参照的目的，存在安装复杂、成本高的不足。同时，该方法其无法用于统计多车辆通过桥梁时，识别车辆数或识别车流量。技术实现要素：本发明的发明目的是，针对上述问题，提供基于桥梁动应变识别车队车辆数的方法，通过提供一种具有安装简便、成本低、效率高的车队车辆数的识别方法，其通过安装一个动应力传感器即可以满足对通过桥梁车流量的测量需求。现有技术中对桥梁车流量统计通常使用车流量检测器进行统计，但成本使用成本较高；本发明通过基于桥梁动应变识别车队车辆数提供了一种成本低廉，安装方便的车队车辆数的方法或车流量的测量方法，为桥梁试验检测、健康监控提供了适合的技术方案。为达到上述目的，本发明所采用的技术方案是：基于桥梁动应变识别车队车辆数的方法，其特征在于，所述桥梁结构形式为梁式桥，梁式桥计算跨径L与车队车辆前后最小间距l需满足关系式在多车辆车队通过桥梁时对该车队车辆数的测量步骤为：所述动应变传感器在设置截面上并沿桥梁的纵向布置；所述动应变传感器通过屏蔽电缆依次连接高速采集器和处理单元；所述高速采集器对动应变传感器的应变信号进行采集并发送到处理单元中；所述处理单元对应变信号进行滤波处理并得到动应变时程曲线，提取得到动应变时程曲线的连续正应变发生区间，并对正应变发生区间内的动应变时程曲线进行二阶求导处理得到荷载系数曲线；所述处理单元根据荷载系数曲线和幅度阈值确定并提取荷载系数曲线上与车队中的单车对应的曲线区间，计算该曲线区间的幅度大小；所述幅度阈值为满足桥梁测量需求的最小单载荷通过所述桥梁时，其对应荷载系数曲线中最小单载荷对应的曲线区间的幅度大小；所述曲线区间满足其幅度大小不小于幅度阈值大小；所述车队车辆数为曲线区间的个数。本方案的重点在于获取荷载系数曲线从而得到车辆数，具体是通过动应变传感器取得应变信号数据，滤波处理，得到动应变时程曲线，建立对应的二维坐标系，确认并提取车辆通过的连续的正应变发生区间，保证数据准确性，且减少运算工作，提高工作效率；通过对正应变发生区间内的动应变时程曲线进行二阶求导获取荷载系数曲线。荷载系数曲线为车队单车通过动应变传感器测试点时，对应应变变化值突变时对应的车辆荷载大小相关系数曲线，每个车辆通过测试点时引起的应变时唯一的；这里具体是将车队单车作为单个集中载荷看待。处理单元根据荷载系数曲线和幅度阈值确定荷载系数曲线上与车队的单车对应生成或引起的曲线区间，并计算该曲线区间的幅度大小，该幅度大小为最大曲线区间幅度大小。幅度阈值为满足桥梁测量需求的最小单载荷通过所述桥梁时，其对应荷载系数曲线中最小单载荷对应的曲线区间的幅度大小。这里幅度阈值保证选取车队单车对应曲线区间的正确性，具体是筛除由于车辆行驶过程中的振动或桥梁振动造成的动应变影响，减少误差影响。根据荷载系数曲线中，车队单车对应的曲线区间都是唯一的，即幅度大小都是唯一的，即可以通过幅度阈值确定荷载系数曲线上与车队的单车对应的曲线区间，并统计该曲线区间数量，即可以获取车队的车辆数。这里幅度阈值可以筛除由于车辆行驶过程中的振动或桥梁振动造成的动应变影响。相比之下，现有技术获取车辆数一般采用车流量检测器，车流量检测器的装置结构复杂，成本较高，维护成本高；而本发明通过基于荷载系数曲线识别车队车辆数提供了一种成本低廉，安装方便的车队车辆数的方法。其中，由于桥梁受力结构形式多样，如有受弯的梁式桥、受压的拱式桥、受拉斜拉桥和悬索桥，经试验比对及受力分析，由于梁式桥广泛的适用性，其受力结构简单、传力路径明确、作用力与结构反应线性关系良好等优点，采用动应变识别车队总重或单车车重有着较好力学基础和较高的适用性和识别精度，经试验验证及比对分析，梁式桥计算跨径L与车队车辆前后最小间距l需满足关系式时，识别准确度可满足桥梁试验检测及健康监控领域的需要。优选的，车辆作用下的桥梁动应变数值大小及波动幅值受诸多影响，只有当车辆总重达到一定数值时，在现有的技术水平和仪器设备条件下，采用动应变识别车队总重或单车车重才能有着一定的适用性和准确度。根据大量的试验验证，当采用高分辨率应变传感器(分辨率不大于0.1με)进行动应变采集，车队总重作用下的桥梁最大应变需满足(Mmax为车辆作用下的桥梁应变测试截面的最大弯矩，ymax为边缘距离中性轴的最大高度，IE为应变测试截面的抗弯刚度)时，该方法具有普遍可接受的准确度。优选的，实测的动应变时程曲线包含较大的环境噪声与系统噪声，未经降噪处理不能作为识别的原始数据，综合应变时程曲线的影响因素与特点，本方法所采用的滤波降噪方法为限幅消抖滤波。优选的，所述动应变时程曲线由处理单元通过有限元仿真计算理论动应变，并提取动应变结果形成。由于采用上述技术方案，本发明具有以下有益效果：1.本发明适合于新旧桥梁的安装检测，对桥梁或道路路面本身没有伤害，无需中断交通即可以完成安装。2.本发明仅在跨中或应变最大截面处布置1个应变监测断面，所以的整体安装成本低且安装方便。3.本发明仅需一条动应变时程曲线来识别车队车辆数或桥梁车流量，因此分析识别更加迅速、快捷、能耗更低，增加了数据处理的时效性。附图说明图1是本发明单个集中荷载作用下的简支梁降噪滤波后的应变时程曲线。图2是图1的一阶导函数图。图3是图1的二阶导函数图。图4是本发明单载荷和多载荷应变时程曲线。图5是图4中多载荷应变时程曲线一阶导函数图。图6是图4中多载荷应变时程曲线二阶导函数图。图7是本发明实施例实测应变时程曲线图。图8是本发明实施例正应变发生区间内动应变时程曲线包络的面积。图9是本发明实施例车队单车车距识别示意图。图10是本发明实施例应变时程曲线导函数图。具体实施方式以下结合附图对发明的具体实施进一步说明。基于桥梁动应变识别车队车辆数的方法，其特征在于，所述桥梁结构形式为梁式桥，梁式桥计算跨径L与车队车辆前后最小间距l需满足关系式在多车辆车队通过桥梁时对该车队车辆数的测量步骤为：所述动应变传感器在设置截面上并沿桥梁的纵向布置；所述动应变传感器通过屏蔽电缆依次连接高速采集器和处理单元；所述高速采集器对动应变传感器的应变信号进行采集并发送到处理单元中；所述处理单元对应变信号进行滤波处理并得到动应变时程曲线，提取得到动应变时程曲线的连续正应变发生区间，并对正应变发生区间内的动应变时程曲线进行二阶求导处理得到荷载系数曲线；所述处理单元根据荷载系数曲线和幅度阈值确定并提取荷载系数曲线上与车队中的单车对应的曲线区间，计算该曲线区间的幅度大小；所述幅度阈值为满足桥梁测量需求的最小单载荷通过所述桥梁时，其对应荷载系数曲线中最小单载荷对应的曲线区间的幅度大小；所述曲线区间满足其幅度大小不小于幅度阈值大小；所述车队车辆数为曲线区间的个数。其中，为了提高上述测量方法的准确性，上述方法应优先应用在桥梁结构形式为梁式桥的桥梁上，并且该桥梁应该满足：车队总重作用下的桥梁最大应变Mmax为车辆作用下的桥梁应变测试截面的最大弯矩，ymax为边缘距离中性轴的最大高度，IE为应变测试截面的抗弯刚度。动应变传感器为高分辨率应变测试装置，其分辨率小于0.1με。其中，处理单元对应变信号进行限幅消抖滤波处理，并通过有限元仿真计算理论动应变提取动应变结果形动应变时程曲线，并建立对应的二维坐标系。在下述进一步说明中，具体是在桥梁1/2跨径处布置动应变传感器，动应变传感器通过屏蔽电缆依次连接高速采集器和处理单元，处理单元为对桥梁监控的计算机。涉及的桥梁参数均采用即εmax＝5；涉及到的桥梁与车辆均满足：桥梁跨径L与车队车辆前后最小间距l：动应变传感器为分辨率等于0.05με；以此进行原理及举例说明。为了进一步了解上述方案工作原理，这里通过简支梁应变时程曲线函数进行说明。单个集中荷载作用下的简支梁降噪滤波后的应变时程曲线可表示为：其中，t为时间，L为简支梁计算跨径，v为速度，测点传感器与所在截面中性轴的距离为y，E是简支梁弹性模量，I是简支梁截面惯性矩。对上式求导得到：式(2)为常函数不连续函数，继续对其求导有：分别作式(1)，式(2)，式(3)函数图如图1-3所示，由图1可知应变曲线的峰值点对应的是荷载P经过动应变传感器测点C所在的截面时，所引起的应变大小，同时测点C所在的截面也是应变时程曲线由上升转为下降的分界点，对应图2中的导数值由正值变为负值。这说明在测点处的应变变化值发生了突变，而引起应变突变的原因是集中荷载依次作用于测点所在截面的左右两侧，根据应变与力对应一定的弹性关系，应变变化值的大小在某种程度上与对应的荷载大小是成正比的，因此对于图3所示的二阶导数值与荷载P的大小是一一对应的。对于多个单位集中荷载作用下的应变函数其一阶及二阶导函数的表达式，如下式(4)，式(5)，式(6)所示。其中，t为时间，N为正整数，即单位荷载数量。其中，t为时间，N为正整数，即单位荷载数量。其中，t为时间，N为正整数，即单位荷载数量。这里假设N＝4，即有4个荷载，载荷方程依次为ε1(x)、ε2(x)、ε3(x)和ε4(x)，则根据式(1)和式(4)分别作出ε1(x)、ε2(x)、ε3(x)和ε4(x)的单载荷函数图和多载荷函数图，如图4上部分所示。由图4可以看出每一个载荷P都对应一个完整的应变影响线曲线，以ε1(x)为例，它表示荷载P1是在原点x＝0处进桥，在时间x＝d3处出桥，对应的d3为实际桥梁计算跨径L。此时对于多载荷下实测的应变时程曲线总长度为(d1+d2+d3)，实测应变ε(x)的总大小为(ε1(x)+ε2(x)+ε3(x)+ε4(x))。对x做时间变换x＝vt，v为车速，便得到总的应变时程曲线图如图4下部分所示。再对实测总应变时程曲线函数二次求导便得到应变变化值突变时对应的车辆载荷大小的荷载系数曲线，如图6所示。这里值得指出的是对于应变时程曲线二阶导值为正时是载荷进桥或出桥时所引起的跨中或最大应变反应处测点应变值开始变大，负值对应的则是荷载经过测点时引起的应变开始变小。对于载荷经过测点C时的应变时程曲线二阶导数值在极短的时间Δt内为一不变常量，即形成荷载系数曲线中确定的曲线区间，该曲线区间对应幅度为单位载荷经过测点时的时程曲线二阶导数值。在实际的检测中，动应变传感器中存在不同的噪音干扰，处理单元可以根据荷载系数曲线和幅度阈值确定荷载系数曲线上与车队的单车对应的曲线区间，并计算该曲线区间的幅度大小，幅度阈值为可测量最小吨位车辆通过所述桥梁确定的荷载系数曲线中负方向上最小幅度值。幅度阈值用于消除该噪音影响。因此，在实际的测量中，在符合上述桥梁参数要求的桥梁上布置好动应变传感器后，通过高速采集器对动应变传感器检测到应变信号采集并发送到处理单元中。处理单元对应变信号进行限幅消抖滤波处理，得到动应变时程曲线，对应该动应变时程曲线并建立对应的二维坐标系。处理单元提取得到动应变时程曲线的连续正应变发生区间，并对正应变发生区间内的动应变时程曲线进行二阶求导处理得到荷载系数曲线。这里二维坐标系的原点或横坐标由该桥梁无车通过时生成动应变时程曲线确定；正应变发生区间可以保证该桥梁有车通过。处理单元根据荷载系数曲线和幅度阈值确定通过桥梁的车队的车辆数为该曲线区间的个数。幅度阈值为满足桥梁测量需求的最小单载荷通过所述桥梁时，其对应荷载系数曲线中最小单载荷对应的曲线区间的幅度大小，即是参数物理意义与前述相同。这里最小单载荷应该满足在Mmax取最小值时，其为桥梁受到的载荷大小。车队中单车荷载的重量大小，或者单车辆车重由式(7)可得：其中为N为正整数，即车队中车辆数量，GVW为车队总重。具体的，处理单元根据荷载系数曲线确定通过该桥梁的车队中，车队单车车重为＝(车队的单车对应的幅度大小/车队的所有单车对应的幅度大小之和)×车队总重；所述车队总重为为正应变发生区间内动应变时程曲线包络的面积×常系数。常系数＝标准吨位的车辆车重/(标准吨位的车辆通过该桥梁得到的正应变发生区间内动应变时程曲线包络的面积)。这里标准吨位的车辆采用10吨、20吨、30吨、40吨等任一组合而成的多辆车辆组成的车队以匀速通过该桥梁得到的正应变发生区间内动应变时程曲线包络的面积。该车队的平均车速由式(8)可得：L为桥梁计算跨径，t1为车辆从进入桥梁到到达测点的时间。具体的，处理单元根据荷载系数曲线确定通过该桥梁的车队中，车速为该桥梁跨度/正应变发生区的负方向第一个曲线区间到正应变发生区间起始点的间距的两倍。该车队单车间距由式(9)可得：Δd＝v(tn-tn-1)＝v·Δt式(9)；v为车速，Δt为单车通过测点的时间间隔。具体的，处理单元根据荷载系数曲线确定通过该桥梁的车队中，单车间距＝[所述桥梁的跨径/(正应变发生区的正方向第一个曲线区间到正应变发生区间起始点的间距的两倍)]×两曲线区间之间间距。以下以实际试验作进一步举例说明。首先取同一车重的多辆小车，这里以20吨模型(4.6kg)车组成车队为例，取20T—20Hz简支梁跨中应变AI01(左边)和AI02(右边)，两点进行速度的识别，识别分为3个等级，20km/h(0.29m/s)，40km/h(0.56m/s)，和60km/h(0.83m/s)。图7中，横轴表示时间，采样频率为20Hz，每小格时间间隔为0.05秒，其中AI01线正应变值为127格，过桥时间为127×0.05＝6.35秒；AI02线正应变为128格，过桥时间为128×0.05＝6.4秒。相对误差20t-20Hz时间s识别速度m/s相对误差％20km/h6.40.3157.540km/h3.30.6067.660km/h2.30.8694.7如图8所示，利用相关软件求得3个20t车重(ε-vt)围成面积为232.38m×ε，常系数为232.38/13.8＝16.84。车重的识别以应变时程曲线与坐标轴包络的面积计，现以车重识别分四个等级，20t(4.6kg)，40t(8.85kg)，60t(13.42kg)和80t(17.9kg)，其中20t为标准重载，40t，60t，80t为识别重载。车队总重面积m×ε识别车重kg相对误％20t(4.6kg)×3232.3813.8040t(8.85kg)×3445.9526.480.360t(13.42kg)×3704.1641.813.880t(17.9kg)×3910.9554.090.7由上表可知，通过常系数和应变时程曲线与坐标轴所围成的面积可以得到车队总重，其误差可以在规定范围内。如图9所示，以多个同一车队总重，不同车速进行单车车距识别。现在以20t-20Hz，车队单车车距为18cm，车速分别为20km/h(0.29m/s)，40km/h(0.56m/s)，和60km/h(0.83m/s)分别进行车队中单车车距的识别。20t-20Hz识别速度m/s识别时间s识别车距m相对误差％20km/h0.320.50.161140km/h0.6060.250.1521560km/h0.8690.20.1743.4以同一单车车距为18cm，同一车队总重2×20t(4.6kg)，同一车速20km/h(0.29m/s)为例。图10为小车以20km/h，采样频率为20Hz时所提取的应变时程曲线图，如若按照步长为0.05s(即原采样频率)对时程曲线求导函数，由于原始时程曲线图中各个点存在上下波动的情况，所得的结果受曲线噪声影响很大,如图10标注；因此会造成二次导函数也随之上下波动，识别结果难以达到预期效果。这里可通过设置幅度阈值筛选出符合的识别结果，幅度阈值大小为可测量最小吨位车辆通过所述桥梁确定的荷载系数曲线中负方向上最小幅度值。由图10所示，符合曲线区间定义的只有两个，标注1、标注2，这与实际车辆数相符。根据式(7)得到：对单车车重的误差在1.24％，在接受误差范围内。可见，在上述方案下，可以测量得车队单车车重，满足桥梁测量的需要。上述说明是针对本发明较佳可行实施例的详细说明，但实施例并非用以限定本发明的专利申请范围，凡本发明所提示的技术精神下所完成的同等变化或修饰变更，均应属于本发明所涵盖专利范围。当前第1页1 2 3