一种Spark环境下基于多重相空间的短时交通流预测方法与流程

本发明涉及智能交通系统领域，特别涉及一种Spark环境下基于多重相空间的短期交通实时预测方法。

背景技术：

随着我国经济的飞速发展，交通运输业在带来巨大的经济与社会效应的同时，也面临着巨大管理压力。数目巨大的车辆造成交通拥堵，加剧空气污染，减缓交通效率，严重地影响着人们的出行。精确及时的利用交通流信息进行交通流预测，可以帮助管理者做出合理的交通管控方案，为人们的出行决策提供了巨大参考价值。交通流系统是一个十分复杂的非线性系统，且符合混沌理论特性。混沌理论作为研究非线性系统随时间变化的一门科学，可以更好的反应交通流系统的内在规律。现有技术的交通预测方法主要存在以下两个问题：

1)短时交通预测模型都在单机环境下预测，传统的数据库不能满足交通数据的高效存储计算，达到时间延迟，为预测模型的数据处理带来了挑战。如今，我们已经进入了交通大数据时代，数据信息日益丰富，单机环境难以处理海量的大数据。现有技术中Spark作为一个非常优秀的开源的大数据处理框架，参见图1，所示Spark架构的原理框图，该框架基于内存计算来提高数据处理速度，底层运用高性能分布式开源数据库HBase，极大的提高了数据存储能力，在众多领域得到了很广泛的应用。

2)传统算法主要利用浅层交通预测模型，但其并没有考虑交通系统的混沌特性，不能适应不确定性强的短时交通流预测。而传统混沌算法虽考虑混沌特性，但使用单个延迟时间和嵌入维度来进行预测，预测精度并不理想。因此，目前迫切需要一种实时且精确预测道路短期交通流的方法，使人们更自由地选择出行时间，以最大程度地保证拥堵问题的减缓，使得道路交通问题得到进一步的改善。

故，针对目前现有技术中存在的上述缺陷，实有必要进行研究，以提供一种方案，解决现有技术中存在的缺陷。

技术实现要素：

有鉴于此，确有必要提供一种Spark环境下基于多重相空间的短期交通实时预测方法，该方法是在海量的交通流数据信息环境下，利用大数据Spark技术，以及建立多重相空间预测模型，从而对下一时段的交通流数据准确地进行实时预测。

为了解决现有技术的问题，本发明的技术方案如下：

一种Spark环境下基于多重相空间的短时交通流预测方法，包括以下步骤：

步骤(1)：获取某个路段的实时车辆信息，并发送至数据库HBase中；

步骤(2)：根据数据库HBase中存储的历史车辆信息，获取历史交通流数据并存储在数据库中；

步骤(3)：在Spark环境下，构建多重相空间模型，结合历史交通流数据，运用该模型对下一个时段的交通流数据进行预测；

其中，所述步骤(3)进一步包括以下步骤：

步骤(31)：对于某路段R，确定延迟时间集合S_τ，嵌入维度集合S_m，以及对应的权重分配

步骤(32)：根据嵌入维度m_i确定预测交通流时间序列X，再根据延迟时间τ_i得到前置时间序列交通流向量X_f；

步骤(33)：取路段R中的历史交通流数据，依次构成时间序列交通流向量X₁,X₂…X_n,，计算与X_f的相似度并升序排列d₁,d₂…d_n；

步骤(34)：从历史交通流数据中找到与“前置时间序列”最相近的z个“相关时间序列”，即获取前z个距离d₁,d₂…d_z，对应的向量为X₁,X₂…X_z，对应权重分配s＝1，d_m＝min{d₁,d₂…d_z}；

步骤(35)：由时间序列交通流向量及权重分配结合延迟时间权重集合Q_τ，根据公式加权计算得到部分交通流；

步骤(36)：重复步骤(32)至步骤(35)，取每一对{τ，m}为一组相空间，代入计算得到部分交通流向量将这些结果累加得到最终的预测交通流X_v:

优选地，在所述步骤(1)中，进一步包括以下步骤：

利用道路交通监控设备及图像处理算法获取通过车辆车牌信息，并发送至数据库中；

运用数据清洗算法对数据库中的车辆数据进行深度清洗，剔除无效的数据信息。

优选地，所述步骤(2)进一步包括以下步骤：

利用以下公式建立交通信息集合：

其中，C表示车辆收集信息集合，H_i表示第i辆车的车牌号码，N为总的车辆个数，B_i,j表示第i辆车的第j条卡口过车记录对应的卡口编号，T_i,j表示第i辆车的第j条卡口过车记录对应的过车时间，T_low表示设定时间的下限、T_up表示设定时间的上限，M_i表示H_i号车在设定时间段内的车辆总数；

通过以下算法计算卡口间的车辆总数：

其中，l(·)代表布尔表达式，l(true)＝1,l(false)＝0；

对海量的交通流数据中所有路段的车辆信息集合重复的执行上述步骤获得某一路段在某一段时间的车辆总数P_n,m，时间间隔为t，通过以下公式来计算每个路段的交通流：

F_n,m＝P_n,m/t。

与现有技术相比较，本发明具有的有益效果：

1.准确性：本发明采用多对延迟时间和嵌入维度构建多重相空间，形成预测模型，更加科学准确的预测下一时刻的交通流。

2.实时性：本发明采用大数据框架Spark技术，面对大规模的历史样本数据，有助于快速计算和存储数据，有利于下一时刻交通流的实时预测。

附图说明

图1为Spark大数据处理框架架构图；

图2为道路交通流实时监测方法的总体流程图；

图3为构建多重相空间下算法预测总体流程图；

图4为平均互信息量I(τ)关于延迟时间τ的曲线图；

图5为温州市西山东路交通流预测的“交通量-时间”图。

如下具体实施例将结合上述附图进一步说明本发明。

具体实施方式

以下将结合附图对本发明提供的Spark环境下基于多重相空间的短期交通实时预测方法作进一步说明。

本发明技术方案的主要构思是：将某个路段每个时刻的实时车辆数据存储在数据库HBase中，进而可以获取任一时段内的交通流数据。在Spark环境下，构建多重相空间模型，通过当前时段的交通流数据结合历史时段的交通流数据采用多重相空间模型对下一个时段的交通流数据进行预测。从而实现了基于当前交通流数据的城市道路交通流预测。具体地说，为了预测某一路段在未来某时间段的交通流量，我们首先预测包含该交通流量的时间序列(“预测时间序列”)，从该时间序列中提前得到交通流量。对于每一对延迟时间τ和嵌入维度m，得到“预测时间序列”的“前置时间序列”，在历史交通流数据中找到与“前置时间序列”最相近的z个“相关时间序列”，基于这z个“相关时间序列”预测得到“预测时间序列”。这样对于每一对延迟时间τ和嵌入维度m，我们都得到了交通流量，最后将这些预测得到的交通流量综合起来作为该路段的交通流量。

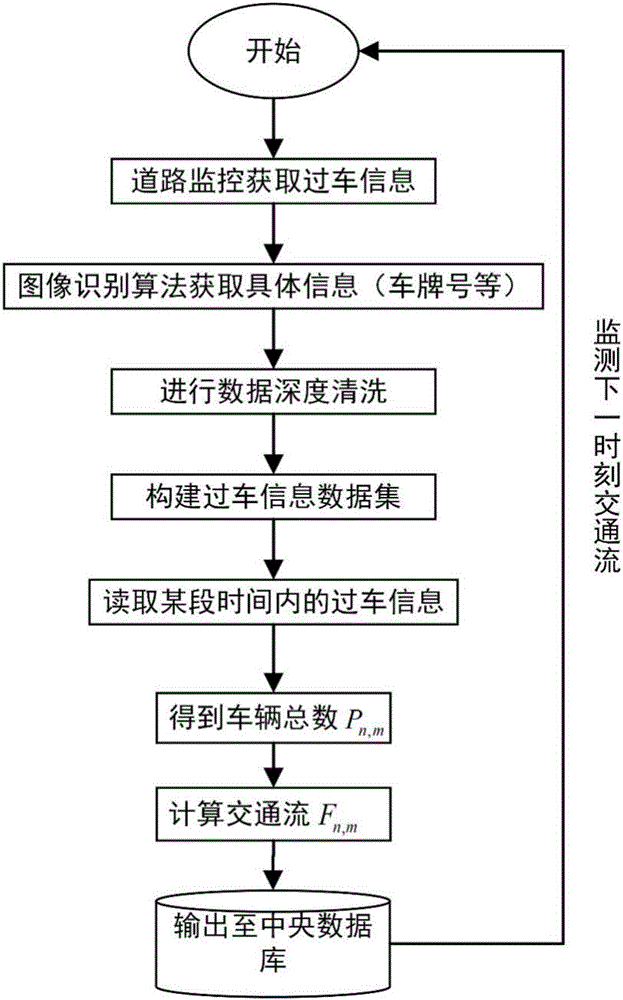
参见图2，所示为本发明方法中获取交通流的步骤流程图，具体包括如下步骤：

步骤(S21).利用道路交通监控设备及图像处理算法获取通过车辆车牌信息，并发送至中央数据库中。

步骤(S22).运用数据清洗相关的算法(异常值清洗，缺失值清洗等)对数据库中的车辆数据进行深度清洗，剔除无效的数据信息(车辆未识别，车牌号码无效等)。

步骤(S23).对上述获取的车辆信息进行分析处理并计算交通流；假设一段道路存在一对卡口B_n，B_m，对于某一个时间段T_i，T_j，时间段满足T_low≤T_i≤T_j≤T_up，设定时间差阈值ε_h，当|T_j-T_i|<ε_h，车辆数P_n,m增加，否则视作停止无效。计算交通流F_n,m＝P_n,m/(T_j-T_i)。

其中，在步骤(S23)进一步包括以下步骤：

步骤(S231)：卡口过车记录为<卡口编号，车牌号，过车时间>。利用以下公式建立交通信息集合：

C表示车辆收集信息集合，H_i表示第i辆车的车牌号码，N为总的车辆个数，B_i,j表示第i辆车的第j条卡口过车记录对应的卡口编号，T_i,j表示第i辆车的第j条卡口过车记录对应的过车时间，T_low表示设定时间的下限、T_up表示设定时间的上限，M_i表示H_i号车在设定时间段内的车辆总数；

步骤(S232)：通过以下算法计算卡口间的车辆总数：

l(·)代表布尔表达式，l(true)＝1,l(false)＝0。

步骤(S233)：对海量的交通流数据中所有路段的车辆信息集合重复的执行步骤步骤(S232)，获得某一路段在某一段时间的车辆总数P_n,m，时间间隔为t，通过以下公式来计算每个路段的交通流。

F_n,m＝P_n,m/t

参见图3，所示为本发明方法中采用多重相空间模型预测的具体流程图，进一步包括以下步骤：

步骤(S31)确定延迟时间集合S_τ，嵌入维度集合S_m，共同组成多重相空间，以及对应的权重分配

其中，步骤(S31)进一步包括以下步骤：

步骤(S311)：通过互信息量法计算延迟时间集合S_τ＝{τ₁,τ₂...τ_nτ}，每一个延迟时间τ对应一个平均互信息量I(τ)，通过实验计算绘制得到平均互信息量I(τ)关于延迟时间τ的曲线图，如图4。下表1显示了曲线图中的部分极小值点。

表1 τ和I(τ)曲线图的部分极小值点

由表1可知，第一个极小值点为τ＝7，I＝3.311，因此该极小值点为最佳延迟时间τ。之后，本文后续选择的极小值点必须小于它的前一个极小值点，于是第二个极小值点为τ＝37，I＝3.305，重复这个过程。最后选择的最佳延迟时间集合Sτ＝{7，37，45，61}，按照如下公式进行权重分配：延迟时间权重集合Q_τ＝{0.68,0.13,0.11,0.08}。

步骤(S312)：设两个随机变量(X,Y)的联合分布为p(x,y),边际分布分别为p(x),p(y),互信息I(X；Y)是联合分布p(x,y)与乘积分布p(x)p(y)的相对熵，即

步骤(S313)：Grassberger和proeaeeia根据嵌入理论和重构相空间的思想，首先提出了从数据序列直接计算嵌入维度的方法，通常称为G-P法。通过G-P法直接计算嵌入维度m，根据某个延迟时间和已知的交通流时间序列，构建一个嵌入维度为m的多维状态向量的嵌入空间，其中，表示路段i在时间段t_j内的交通流量，p为总的时间段个数。求解两个向量之间的向量距离，并且规定只要是距离小于给定的正数ε的矢量，成为有相互关联的矢量，这些相互关联的矢量占总矢量的比例作为重构m维相空间的关联积分：其中，H是赫维赛德阶跃函数，d_i,j是欧拉范式，它是向量X_i和X_j之间的距离，表示相似度。最后定义关联维数D₂，混沌时间序列的关联维数D₂会随着嵌入维度m增加而收敛，非混沌时间序列的关联维数D₂会随着嵌入维度m增大而离散。因此可用嵌入维度m的收敛性来判断交通流量是否符合混沌理论。根据步骤(S311)的延迟时间集合S_τ，为每一个延迟时间τ计算得到嵌入维度m(τ)，得到嵌入维度集合S_m。

步骤(S32)：根据嵌入维度m_i确定预测交通流时间序列X，再根据延迟时间τ_i得到前置时间序列交通流向量X_f。

步骤(S33)：找到与X_f最相近的z个历史交通流时间序列。

取该路段的历史交通流数据，依次构成时间序列交通流向量X₁,X₂…X_n，计算与X_f的相似度并升序排列。

步骤(S34)：获取前z个距离d₁,d₂…d_z，对应的向量为X₁,X₂…X_z，组成权重分配s＝1，d_m＝min{d₁,d₂…d_z}。

步骤(S35)：由时间序列交通流向量权重分配结合延迟时间权重集合Q_τ，根据公式加权计算得到部分交通流。

步骤(S36)：重复步骤(S32)至步骤(S35),取每一对{τ，m}代入计算得到部分交通流向量，得到最终的预测交通流X_v:

以下以温州市路网中西山东路为例进行详细说明:

我们使用2015年3月25日至3月27日共三天整个温州市路网产生的GPS数据。通过道路监控设备实时获取路段车辆信息，运用图像处理算法获得车辆的具体信息并存储于数据库，得到通过的交通车辆数P_n,m,并通过公式F_n,m＝P_n,m/t计算交通流并存储于数据库中。运用相关算法得到延迟时间集合S_τ＝{7,37,45,61}，嵌入维度集合S_m＝{5,8,10,11}，权重集合Q_τ＝{0.65,0.14,0.12,0.09}，要预测某卡口对在8:00～8:10的交通流F_8:00～8:10，首先取τ＝7,m＝5。根据m＝5，预测交通流时间序列X＝{F_7:20～7:30,F_7:30～7:40…F_8:00～8:10}，根据τ＝7，则前置交通流时间序列X_f＝{F_6:10～6:20,F_6:20～6:30…F_6:50～7:00}，从历史交通流序列中找到与X_f最相近的z个时间序列，并由此预测得到一个交通流F_8:00～8:10值。每对延迟时间和嵌入维度代入预测得到一个交通流F_8:00～8:10值,通过加权平均得到最终的F_8:00～8:10值。

图5展示了在3月27日下本文算法，预测结果及传统算法之间的效果比较，预测时间为6:00～18:00，本文算法预测值与实测值准确度很高，传统算法相差较大，且数据不稳定。

综上所述，本发明是通过实时监测交通数据，预处理后实时存入数据库中，通过本方法的公式F_n,m＝P_n,m/t计算出每条道路的交通流并存储在HBase中，由多重相空间算法模型预测得出某路段下一时段的交通流。该方法具有准确性和实时性等特点，克服了传统的交通预测模型在大数据背景下预测获得道路交通流的方法在实时性，准确性方面的不足。

以上实施例的说明只是用于帮助理解本发明的方法及其核心思想。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以对本发明进行若干改进和修饰，这些改进和修饰也落入本发明权利要求的保护范围内。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。