可优化的自适应多核支持向量机的短时交通流预测方法与流程

本发明涉及机器学习和智能交通领域，特别是一种可优化的自适应多核支持向量机的短时交通流预测方法。

背景技术：

交通流诱导与控制是智能交通系统(its)的基本功能，通过发布实时有效的交通出行信息，诱导出行者选择最佳出行路径，避免向拥堵区域的进一步集聚，引导和均衡交通流在时间与空间上的分布，实现对交通拥堵的主动式控制，可有效提高路网通行效率、缓解城市交通拥堵，同时减轻由此产生的环境污染和资源浪费问题。而交通流诱导与控制系统的正常运行，核心基础就在于短时交通流的实时、动态和精准预测。

目前为止，国内外业已提出的交通流预测方法主要有时间序列法、卡尔曼滤波、混沌理论、神经网络和支持向量机(svm)等。影响交通流变化的因素多种多样，而且彼此之间具有非线性和随机性的特点。svm具有良好的自学习和非线性预测能力，并且能在小训练样本的情况下获得较好的预测精度，因此在短时交通流预测领域拥有举足轻重的地位。svm是一种针对分类和回归问题的统计学习方法，其建立在vc维理论和结构风险最小化原则之上，用于解决小样本和过度学习问题，能够保证所求极值是全局最优解。然而，现有基于svm的方法在实际预测时本质上只采用了一种核函数，不足以充分适应交通流的变化特征。为提高预测结果的准确率，有必要对算法做进一步的改进并提出更好的预测模型。

技术实现要素：

本发明的目的在于提供一种可优化的自适应多核支持向量机的短时交通流预测方法，该方法可改善现有支持向量机(svm)方法仅采用单个核函数进行预测的不足，能充分适应交通流非线性和随机性的变化特征，实现对短时交通流的实时、自适应预测，同时提高预测结果的速度和精度，具有一定的理论参考和现实意义。

为实现上述目的，本发明的技术方案是：一种可优化的自适应多核支持向量机的短时交通流预测方法，包括如下步骤，

步骤s1：组合高斯核函数和多项式核函数以构建自适应多核支持向量机；

步骤s2：利用自适应粒子群算法对自适应多核支持向量机进行参数优化；

步骤s3：同时考虑历史数据和实时数据，提出基于自适应多核支持向量机的短时交通流预测模型；

步骤s4：输入交通流数据集，利用预测模型生成短时交通流的预测结果；

步骤s5：根据交通流的预测结果和实际交通数据，对预测误差进行评价分析。

在本发明一实施例中，在所述步骤s1中，所述自适应多核支持向量机通过如下方式构建：

步骤s11：构建高斯核函数与多项式核函数组合而成的混合核函数：

k(x,xi)＝β·exp(-γ||x-xi||²)+(1-β)·[γ(x·xi)+1]^q

其中，x和xi表示样本集中任意两个实输入向量，β∈[0,1]为混合核函数的权重系数，γ为核函数的固有参数，q为幂次；

步骤s12：根据交通流的实时变化趋势即数值的斜率大小来自适应调整权重：

其中，表示之前两个时段交通流量值在二维平面上所对应点(xi-1,yi-1)和(xi-2,yi-2)的斜率。

在本发明一实施例中，在所述步骤s2中，所述自适应粒子群算法采用自适应的惯性权重、学习因子和飞行时间因子随惯性权重动态调整的学习策略；自适应粒子群算法中每个粒子的当前位置为待定参数的当前值：χ＝(c,ε,γ)，通过优化过程搜索得到所需的自适应多核支持向量机的最优参数。

在本发明一实施例中，在所述步骤s3中，所述的短时交通流预测模型具体流程如下：

步骤s31：初始化自适应粒子群环境参数；

步骤s32：将待求参数当作粒子的位置向量，并初始化粒子速度和位置；

步骤s33：输入历史平均交通流数据到训练模块，通过自适应多核支持向量机进行映射和回归；

步骤s34：计算粒子的适应度值，并按照更新粒子的速度和位置；

步骤s35：针对每个粒子，重复步骤s32～s34；

步骤s36：按照步骤s33～s35进行迭代更新，直到样本的训练误差满足精度限制，此时输出最优参数c、ε和γ到预测模块；

步骤s37：输入前n个时段的实时交通流数据到预测模块：x＝[xt-n,…,xt-1,xt]，根据实时数据计算β值，然后在最优参数条件下训练自适应多核支持向量机，并预测输出下一时段的交通流量。

在本发明一实施例中，在所述步骤s4中，对交通流数据集进行预处理，输入到步骤s3中所述的预测模型，模型经优化和训练后输出目标路段在下一时段的短时交通流预测值。

在本发明一实施例中，所述步骤s5中，采用以下的评价标准对预测误差进行评价分析：

1)平均绝对百分误差(mape)：

2)均方根误差(rmse)：

3)相关系数(r)：

其中，yi为实际交通量，为预测的交通流量，n为样本个数。

相较于现有技术，本发明具有以下有益效果：本发明所提出的一种可优化的自适应多核支持向量机的短时交通流预测方法，可改善现有svm方法仅采用单个核函数进行预测的不足，能充分适应交通流非线性和随机性的变化特征，实现对短时交通流的实时、自适应预测，同时提高预测结果的速度和精度。

附图说明

图1是本发明实施例中基于可优化的自适应多核支持向量机的短时交通流预测模型。

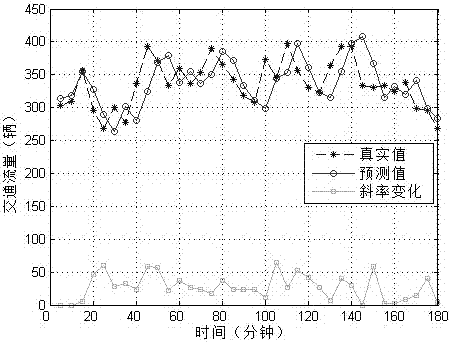
图2(a)是本发明实施例中利用所发明的方法预测生成的某路段在高峰期的短时交通流量。

图2(b)是本发明实施例中利用自适应混合核函数与固定混合核函数对高峰期短时交通流预测的性能评价指标。

图3是本发明实施例中所发明的方法与现有技术对短时交通流预测结果的对比。

具体实施方式

下面结合附图，对本发明的技术方案进行具体说明。

本发明提出一种可优化的自适应多核支持向量机的短时交通流预测方法，具体按照如下步骤实现：

步骤s1，组合高斯核函数和多项式核函数以构建自适应多核支持向量机。

在本实施例中，由于不同特征空间中数据的分布不同，支持向量机的性能很大程度上取决于核函数的选择。核函数按类型可分为局部核函数和全局核函数，局部核函数学习能力强，但泛化能力比较弱；全局核函数泛化能力强，学习能力则相对较弱。高斯径向基核函数(rbf)和多项式核函数(poly)分别为典型的局部核函数、全局核函数，因此它们经常被用于交通流预测。两者的公式如下：

k(x,xi)＝exp(-γ||x-xi||²)(1)

k(x,xi)＝[γ(x·xi+1)]^q(2)

其中，(1)式为rbf，(2)式为poly，x和xi表示样本集中任意两个实输入向量，γ为核函数的固有参数并决定了数据映射到新的特征空间后的分布，q为poly的幂次。为适应交通流的非线性和随机性，同时提高预测结果的可靠性和准确性，本发明的自适应多核支持向量机采用高斯核函数与多项式核函数组合而成的混合核函数，表达式如下：

k(x,xi)＝β·exp(-γ||x-xi||²)+(1-β)·[γ(x·xi)+1]^q(3)

其中，β∈[0,1]为混合核函数的权重系数。

进一步的，为充分利用两者的优势，本发明根据交通流的实时变化趋势即数值的斜率大小来自适应调整权重，公式如下：

其中，表示之前两个时段交通流量值在二维平面上所对应点(xi-1,yi-1)和(xi-2,yi-2)的斜率。当斜率|k减小时，曲线趋于平坦，此时应增强核函数的全局泛化能力，即增大多项式核函数的权重，对应减小β的值；当斜率|k|增大时，曲线趋于尖锐，此时应增强核函数的局部学习能力，即增大高斯核函数的权重，对应增大β的值。

步骤s2，利用自适应粒子群算法对amsvm进行参数优化。

在本实施例中，已知待定参数包括：惩罚系数c、不敏感损失系数ε和参数γ，q值选取为2。apso的主要思想是采用自适应的惯性权重，同时令学习因子和飞行时间因子随惯性权重动态调整。优化模型时，令apso中每个粒子的当前位置为待定参数的当前值：χ＝(c,ε,γ)，则通过算法优化过程搜索到的全局最优位置即为向量中元素的最优解，亦即所求的amsvm最优参数。

步骤s3，同时考虑历史数据和实时数据，提出基于amsvm的短时交通流预测模型。

在本实施例中，目标路段在下一时段的交通流量主要与对应时段的历史平均值、前几个时段的实时值有关。为了准确反映交通流变化规律对预测值的影响，在构建预测模型时，以历史平均交通流数据、前几时段交通流数据作为输入变量。此外，定义回溯系数n表示利用前n个时段的交通数据进行实时预测。首先把输入的历史平均交通流数据当作训练样本，利用本文提出的自适应粒子群算法对amsvm进行参数寻优；然后利用输入的实时数据训练优化后的amsvm，并预测下一时段的交通流量。模型具体流程如下：

1)初始化自适应粒子群环境参数；

2)将待求参数当作粒子的位置向量，并初始化粒子速度和位置；

3)输入历史平均交通流数据到训练模块，通过amsvm进行映射和回归；

4)计算粒子的适应度值，并按照更新粒子的速度和位置；

5)针对每个粒子，重复步骤2)～4)；

6)按照步骤3)～5)进行迭代更新，直到样本的训练误差(即适应度值)满足精度限制，此时输出最优参数c、ε和γ到预测模块；

7)输入前n个时段的实时交通流数据到预测模块：x＝[xt-n,…,xt-1,xt]，根据式(4)计算β值，然后在最优参数条件下训练amsvm，并预测输出下一时段的交通流量。

步骤s4，输入交通流数据集，利用预测模型生成短时交通流的预测结果。

在本实施例中，对交通流数据集进行预处理，输入到步骤s3中的预测模型，模型经优化和训练后输出目标路段在下一时段的短时交通流预测值。

步骤s5，根据交通流的预测结果和实际交通数据，对预测误差进行评价分析。

在本实施例中，采用以下的评价标准对预测误差进行评价分析：

1)平均绝对百分误差(mape)：

2)均方根误差(rmse)：

3)相关系数(r)：

其中，yi为实际交通量，为预测的交通流量，n为样本个数。平均绝对百分误差和均方根误差越小，表示模型预测结果的精度越高；相关系数越大，表示预测交通流量和实际交通流量的拟合度越好。

为了让本领域技术人员进一步了解本发明所提出的一种可优化的自适应多核支持向量机的短时交通流预测方法，下面结合具体实施例作详细说明。本实施例以本发明技术方案为前提进行实施，给出了详细的实施方式和具体的操作过程。

如图1所示，为基于可优化的自适应多核支持向量机的短时交通流预测模型。

本实施例包括如下具体步骤：

步骤一：由车辆检测器收集目标路段的交通流数据，上传到交通信息中心后，可下载对应的车流量数据。假设要预测目标路段在某周一的短时交通流量，需事先对数据进行预处理。以5分钟为一个周期统计车流量，将一天24小时划分为288个周期。选取之前一周的工作日即周一到周五的交通流量，计算它们的平均值作为训练模块的样本数据。令回溯系数n＝3，即利用当前时刻之前15分钟的实时数据来预测下一时段(即未来5分钟)的交通流量。

步骤二：输入步骤一中的历史平均交通流数据到训练模块。首先对数据进行归一化处理，以减少训练时间、提高模型效率。apso算法的环境变量设置如下：迭代次数为200，种群数量为30，惯性权重取值区间为[0.4,0.9]，学习因子取值区间为[0.8,2]，待优化的参数c、ε、γ的变化区间均设置为[0.001,0.1]，同时令精度限制为10^-4。apso每一次迭代过程中，amsvm对训练样本进行交叉验证，直到训练误差满足精度限制。优化结束后，可得到模型的最优参数c、ε和γ分别为0.086、0.021和0.045。

步骤三：输入实时交通流数据和最优参数到预测模块。根据当前时刻之前两个时段的流量值计算斜率，并根据式(4)计算此时的混合核函数的权重，由此确定预测下一时段流量值时所使用的核函数的构成。基于最优参数和自适应核函数，利用amsvm映射和回归当前时刻之前15分钟(即3个时段)的流量数据，并预测输出下一时段的交通流量。

如图2所示，是利用所发明的方法预测生成的目标路段在高峰期的短时交通流量和性能评价指标。

本实施例包括如下具体步骤：

步骤一：输入目标路段在高峰期(15:00-18:00)对应的历史平均交通流数据到训练模块，经优化后，得到模型的最优参数c、ε和γ分别为5,0.01和0.002。图2(a)所示为高峰期交通流量的预测结果，其中最底部的线表示实际交通流数值的斜率大小，其变化趋势可以间接反映混合核函数的变化过程。与此同时，固定参数c、ε和γ值不变，使权重β在[0.0,1.0]区间取值，得到图2(b)所示的预测性能比较。

步骤二：由图2(a)可知，本发明的可优化的自适应多核支持向量机，可以灵活适应交通流的非线性和随机性特征。由图2(b)可知，相比于固定的混合核函数权重，拥有自适应权重的amsvm具有更低的平均绝对百分误差和均方根误差，以及更高的相关系数。由此说明amsvm在自回归预测的可行性和优越性。

如图3所示，为所发明技术与现有技术对短时交通流预测结果的对比。

本实施例包括如下具体步骤：

步骤一：为了进一步说明本发明的优势，选取现有技术中的pso-svm,apso-svm-r和apso-svm-p与apso-amsvm进行比较。不失一般性地，图3仅展示这些方法对高峰期交通流的预测结果。表1为这些方法对24小时交通流预测性能的评价指标。

表1不同方法交通流预测结果的性能比较

步骤二：由表1可知，apso-amsvm方法的mape、rmse分别为10.2608％和12.3632％，两者均低于其它三种方法。同时，其r值为0.9654，高于其它三种方法。由此说明，相比于现有技术，本发明在预测短时交通流时拥有更高的精度。

上述分析说明，本发明所提出的基于可优化的自适应多核支持向量机的短时交通流预测模型，能够很好的实现短时交通流的预测，具有一定的具有一定的理论参考和现实意义。

以上是本发明的较佳实施例，凡依本发明技术方案所作的改变，所产生的功能作用未超出本发明技术方案的范围时，均属于本发明的保护范围。