粒子群算法优化LSTM神经网络的行程时间预测方法与流程

本发明涉及深度学习方法和行程时间预测等技术领域，具体涉及一种粒子群算法优化lstm神经网络的行程时间预测方法。

背景技术

车辆路段行程时间预测是交通管理部门采取交通控制和诱导措施的重要依据。通过对行程时间的预测，可以提前调整交通管理控制手段，提高交通运行效率，同时对车辆诱导有重要作用。行程时间数据是时间序列数据，随着机器学习及深度学习的推进，对行程时间的预测方法也在不断改善。

在统计特性研究层面，有趋势外推法、线性回归、隐形马尔科夫预测模型及卡尔曼滤波等。在机器学习方法层面，通过挖掘历史数据隐含的信息，实现行程时间的迭代估计。支持向量机、迭代决策树、随机森林、贝叶斯网络、小波理论、改进粒子群算法对bp神经网络等不同模型都应用在行程时间预测中。

在深度学习中，采用深度信念网络对数据先进行特征学习提取，再采用顶层svm模型进行预测。对lstm神经网络模型调参方法有精细化调参、多网格搜索、根据经验设置等方法。

在行程时间预测领域，当前流行的方法是采用lstm神经网络进行预测，但该方法需要对lstm神经网络的多种参数进行调整，才能拥有较高的预测精度。目前对于lstm神经网络预测模型参数选取研究多是采用遍历多网格搜索算法、控制变量精细调参，本质都是暴力搜索寻找最优值，计算资源消耗量大。

技术实现要素：

本发明的内容就是在解决在lstm神经网络行程时间预测中，由于大范围参数组合寻优带来的计算资源消耗大，预测性能较差，无法寻到lstm神经网络最优参数组合的问题。

为实现上述目的，本发明的技术方案是：

一种粒子群算法优化lstm神经网络的行程时间预测方法，包括如下步骤：

步骤s1：采集行程时间数据，进行数据归一化，按比例划分为训练集和测试集；

步骤s2：采用粒子群算法优化lstm神经网络预测模型的各个参数；

步骤s3：输入粒子群算法优化好的参数、训练集，进行lstm神经网络预测模型的迭代优化；

步骤s4：利用已训练好的lstm神经网络模型对测试集进行预测，并评估模型误差。

进一步地，所述步骤s1具体为：

采用高速公路进出口收费站对行驶车辆信息收集，并分为30分钟、60分钟两个不同间隔的行程时间数据；

对数据进行归一化，并按照比例划分为训练集和测试集。

进一步地，所述数据归一化方法采用min-max标准化，公式如下：

其中，x*是归一化后的行程时间数据，x为收集的行程时间数据，max为样本数据的最大值，min为样本数据的最小值。

进一步地，所述步骤s2中，lstm神经网络预测模型的所需优化参数包括：lstm神经网络隐藏层数、时间窗步长、训练次数、学习率，所述粒子群算法优化lstm神经网络的模型是在参数搜索空间里，以预测误差最小为目标函数，对参数组合进行优化。

进一步地，所述在参数搜索空间里，以预测误差最小为目标函数，对参数组合进行优化具体包括：

步骤s21、初始化，初始搜索点的位置及其速度通常是在允许的范围内随机产生的，每个粒子的pbest坐标设置为其当前位置，且计算出其相应的个体极值，即个体极值点的适应度值，而全局极值，即全局极值点的适应度值，就是个体极值中最好的值，记录该最好值的粒子序号，并将gbest设置为该最好粒子的当前位置；

步骤s22、评价每一个粒子，计算粒子的适应度值，若好于该粒子当前的个体极值，则将pbest设置为该粒子的位置，且更新个体极值；若所有粒子的个体极值中最好的好于当前的全局极值，则将gbest设置为该粒子的位置，记录该粒子的序号，且更新全局极值；

步骤s23、粒子的更新，用迭代公式对每一个粒子的速度和位置进行更新；

步骤s24、检验是否符合结束条件，若当前的迭代次数达到了预先设定的最大次数，则停止迭代，输出最优解，否则转到步骤s22；

步骤s25、输入粒子群算法优化好的参数组合、训练集，进行lstm神经网络预测模型的迭代优化。

进一步地，所述步骤s3具体为：

输入粒子群算法优化好的参数组合，采用时间窗步长参数对输入数据进行处理，通过隐藏层数、训练次数、学习率对lstm神经网络进行设置；

将预测均方误差作为lstm神经网络的优化目标，采用adam优化算法进行梯度计算。

进一步地，所述采用adam优化算法进行梯度计算具体为：采用adam优化算法对网络迭代更新不断调整模型权重、降低预测误差，其算法原理为：

mmt为梯度前一时刻平均值，vmt为梯度后一时刻非中心方差值。

参数最终的更新公式如下：

在实际应用中效果较好，通常将β1设置为0.9，β2设置为0.9999，γ设置为10^-8。

进一步地，所述步骤s4具体为：

采用训练好的lstm神经网络模型对预测集进行行程时间预测；

将预测数据同实际数据进行误差计算，误差计算采用均方误差和均方根误差两项指标，还原预测数据进行输出，其中，

均方误差：

均方根误差：

n是数据集个数，yi是真实数据集，yi^*是预测集。

与现有技术相比，本发明的有益效果在于：

1、采用粒子群算法优化lstm神经网络模型参数选择，该方法可以在参数空间快速找到最优组合；

2、采用粒子群算法和lstm神经网络模型预测行程时间，模型适合处理与时间序列相关的问题，提高预测精准度；

3、粒子群算法优化lstm神经网络模型对不同间隔的数据样本具有良好的适用性。

4、对数据预测均方误差和均方根误差最小，模型减少了计算量，表现出更好的预测性能。

附图说明

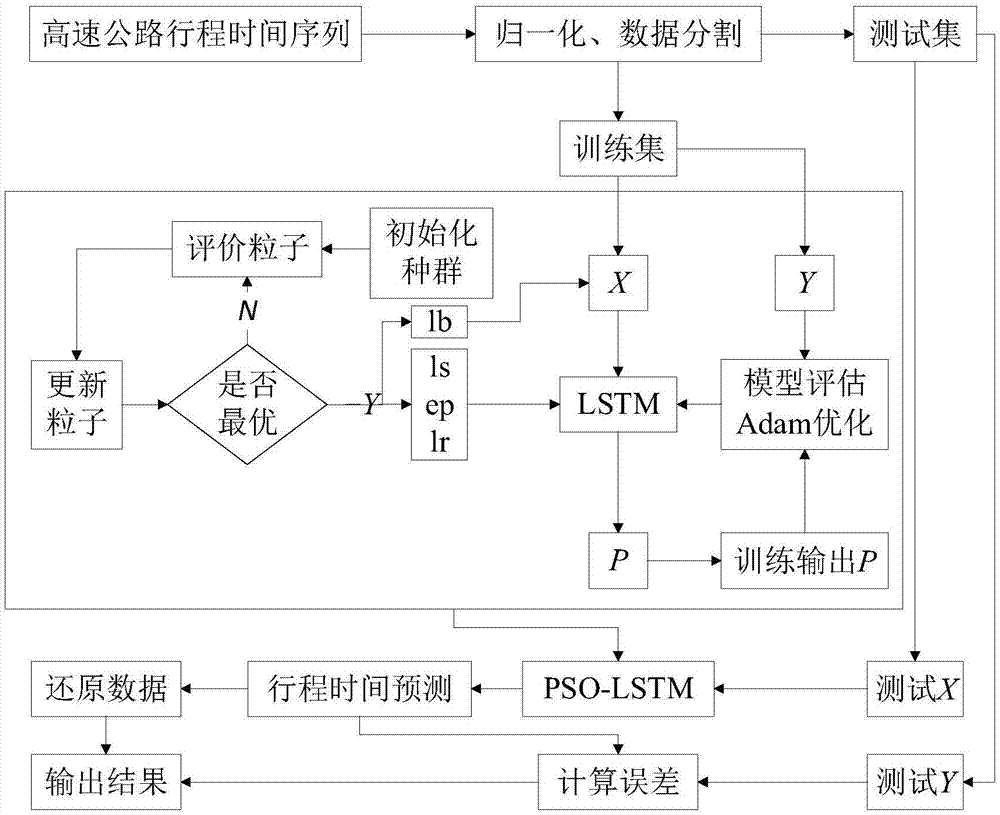
图1是本发明实施例的算法示意图。

图2是粒子群优化lstm神经网络最优值迭代。

图3是四种模型30分钟行程时间预测示意。

图4是四种模型60分钟行程时间预测示意。

图5是四种模型两个对样本预测均方误差。

图6是四种模型两个对样本预测均方根误差。

具体实施方式

下面结合实例对本发明做进一步的说明，所描述的实施例旨在便于对本发明的理解，但对其不起任何限定作用。

如图1所示，一种粒子群算法优化lstm神经网络的行程时间预测方法，包括如下步骤：

步骤s1：行程时间数据采集，并进行数据归一化预处理，分为训练数据集和测试数据集；

所述行程时间数据来源于高速公路收费站采集的车辆信息，获得进出收费站的时间之差，时间间隔可以根据实际预测需求制定，本发明采用的是30分钟、60分钟两个间隔样本数据。读取获得原始行程时间数据，采用min-max标准化方法对数据归一化：

其中，x*是归一化后的行程时间数据，其中max为样本数据的最大值，min为样本数据的最小值。

步骤s2：采用粒子群算法优化lstm神经网络预测模型的各个参数。

粒子群算法对lstm涉及到的参数进行调整优化，获取搜索空间的最优解，形成复合pso-lstm模型，主要流程步骤为：

步骤s21、初始化，初始搜索点的位置及其速度通常是在允许的范围内随机产生的，每个粒子的pbest坐标设置为其当前位置，且计算出其相应的个体极值(即个体极值点的适应度值)，而全局极值(即全局极值点的适应度值)就是个体极值中最好的，记录该最好值的粒子序号，并将gbest设置为该最好粒子的当前位置；

步骤s22、评价每一个粒子，计算粒子的适应度值，若好于该粒子当前的个体极值，则将pbest设置为该粒子的位置，且更新个体极值；若所有粒子的个体极值中最好的好于当前的全局极值，则将gbest设置为该粒子的位置，记录该粒子的序号，且更新全局极值；

步骤s23、粒子的更新，用迭代公式对每一个粒子的速度和位置进行更新；

步骤s24、检验是否符合结束条件，若当前的迭代次数达到了预先设定的最大次数，则停止迭代，输出最优解，否则转到步骤s22；

步骤s25输入粒子群算法优化好的参数组合、训练集，进行lstm神经网络预测模型的迭代优化；

将处理好的测试数据x输入到pso-lstm隐藏层中，输出预测数据为：p，网络训练损失函数采用均方误差。pso-lstm模型中采用经粒子群算法选定好的参数，优化目标为损失函数最小化，采用adam优化算法对网络迭代更新不断调整模型权重、降低预测误差，其算法原理如下：

mmt为梯度前一时刻平均值，vmt为梯度后一时刻非中心方差值。

参数最终的更新公式如下：

在实际应用中效果较好，通常将β1设置为0.9，β2设置为0.9999，γ设置为10^-8。实例证明其收敛速度快且模型精度高，还可以解决学习率消失及收敛过慢问题。

步骤s4：利用已训练好的lstm神经网络模型对测试数据集进行预测，并评估模型误差。

采用训练好的lstm神经网络模型对测试集进行预测，将预测数据同实际数据进行误差计算。还原预测数据进行输出。采用均方误差(mse)和均方根误差(rmse)作为评估指标，在预测中，mse和rmse的值越小，代表预测精度越高。其中，

均方误差：

均方根误差：

n是数据集个数，yi是真实数据集，yi^*是预测数据集。

综上，本发明提出的粒子群算法优化lstm神经网络的行程时间预测方法包括如下步骤：对收费站采集的数据进行归一化处理，分为训练集和测试集；采用粒子群算法对lstm神经网络的模型参数进行优化；对lstm神经网络预测模型进行训练；调用预测模型对测试数据集进行预测并评估预测误差。

本发明提出的粒子群算法优化lstm神经网络的行程时间预测方法利用了粒子群算法和lstm神经网络对参数组合快速寻优的特性，可以得到更高的预测精度，且对不同间隔数据样本有良好的适用性。

本发明的有效性可以通过实施例来进一步说明，实施例的数据不限制本发明的应用范围。

实验平台：处理器为inteli5-6500，内存为8.0gb；系统是windows10(64位)；程序语言版本为python3.6。

实验内容：

本实施例的数据来源于openits所公布的广州市某高速公路的抽样刷卡数据。采取方法为每隔5分钟抽取10个刷卡样本。本实施例的数据量大，真实性高。为了真实对比车辆行程时间，本文选用相同进出口车辆数据。数据采集间隔分别为30分钟，60分钟，能够有效保证管理部门数据预测需求。采用离差标准化方法进行归一化，实验以前8天数据为训练集，后2天数据为测试集。

采用粒子群算法优化lstm模型参数取值，设置群体规模为50，学习因子c1和c2均为2，迭代次数为100，惯性因子w为4，以60分钟行程时间数据进行分析。参数搜索空间：隐藏层数，40-200，步长为10；时间窗步长，4-20，步长为1；训练次数，10-320，步长为10；学习率，0.01-0.032，步长为0.001。

图2表示最优值迭代示意图。在粒子群算法中，随着迭代步数增加，可以在搜索空间快速找到近似最优解，实现搜索空间参数组合的最优解。经过粒子群算法的寻优，确定lstm神经网络的参数组合为：隐藏层数为120，时间窗步长为6，训练次数为160，学习率为0.015。

实验选取了在行程时间预测中常用的模型作为对照：随机森林算法(rf)、支持向量机算法(svm)、最近邻算法(knn)，同本发明的算法(pso-lstm)进行预测性能对比。图3是四种模型30分钟行程时间预测示意，图4是四种模型60分钟行程时间预测示意，图5是四种模型两个对样本预测均方误差，图6是四种模型两个对样本预测均方根误差。

表1为算法行程时间预测性能对比

本发明提出的一种基于粒子群算法优化lstm神经网络的行程时间预测方法，能够获得更好的预测性能，提高了行程时间预测精度。本发明所提出的方法，在两个不同间隔数据中误差均最低，证明了方法具有良好的适用性。

以上是本发明的实施例，但本发明并不局限于上述特定实施方式，凡依本发明技术方案作出的改变，所产生的功能作用未超出本方法技术方案的范围时，其同样应当视作本发明所公开的内容。