一种基于电容扰动的周界报警系统入侵信号识别方法与流程

本发明涉及电容扰动信号处理及识别技术，尤其涉及一种电容扰动围界入侵信号的识别方法。

背景技术

随着社会的发展，机场围界报警系统是机场安全防范系统的重中之重。《民用运输机场安全保卫设施》(mh/t7003-2017)明确规定年旅客吞吐量200万人次以上的一二类机场的飞行区围界应设置围界报警系统和视频监控系统，年旅客吞吐量在50万至200万人次的三类机场宜设置入侵报警系统和视频监控系统。系统应能对物理围界形成完整的覆盖，能对围界入侵行为作出判断，对目标进行分类，应能在机场飞行和安全照明的环境下工作，应满足全天候运行的要求。

电容周界报警系统是一种全新概念的周界报警入侵检测系统，集阻挡和报警两大功能于一体，可实现对指定区域的入侵报警、安全距离报警、24小时不间断实时边界守卫等功能，其可靠性高，实时性好，极大的缓解了保卫人员的工作强度，提高了防护区域的安全性，具有广泛的应用前景。

目前关于电容扰动周界报警的研究较少，专利文献cn104851226a于2015年8月19日公开了一种用于电容扰动周界报警系统和报警方法，只提供了机场耦合电容式报警系统，能满足机场入侵检测的需求，但还是存在一定的误报率和漏报率，现有系统中缺乏对信号的优化处理。

如何确保系统对入侵信号辨识的准确性及如何提供一种高效、实时的入侵检测方法为电容围界报警系统的一个重要研究方向。

技术实现要素：

有鉴于此，本发明提供了一种电容围界入侵信号处理方法，以满足机场范围长距离入侵检测需求，减小系统误警次数和平均漏报次数。

本发明技术方案为一种基于电容扰动的周界报警系统入侵信号识别方法，包括以下步骤：

步骤1、对获取的电容扰动信号进行去噪处理；

步骤2、使用固有时间尺度分解算法itd(固有时间尺度分解算法)和ht变换提取训练样本特征值；

步骤3、构建pnn概率神经网络，将有效的特征量供pnn神经网络训练，经过训练从而调节好pnn概率神经网络的参数，然后将调整好的参数交给概率神经网络分类模块使用；

其中所述步骤1的具体方法为：

步骤1.1根据电容扰动信号和干扰频带经过实验确定分解层数；

步骤1.2采用多个小波滤波器对电容扰动信号进行小波包变换，选取效果最好的一个获得小波包变换系数；

步骤1.3根据原始扰动信号的特点和小波包基函数最佳选取算法，采用自底向顶的方法选取小波基函数；

步骤1.4对最佳正交小波包基对应的小波包系数进行处理；

步骤1.5重构去除噪声后的扰动信号；

所述步骤3的具体方法为：

步骤3.1对输入矩阵进行归一化处理，训练样本的最终特征向量矩阵为

x＝[f,a,t,he]

步骤3.2训练pnn概率神经网络；

步骤3.3采用训练好的pnn概率神经网络对实施信号进行分类识别。

进一步的，所述步骤1.2中小波滤波器包：daubechies小波滤波器、symlets小波滤波器。

进一步的，所述步骤2的具体方法为：

步骤2.1利用固有时间尺度分解算法提取电容扰动信号的固有旋转分量prc和一个残余分量；

步骤2.2经itd分解得到的n个prc分量，每个分量都包含有其各自的频率成分f1,f2,...,fn，其中含有不同的能量e＝{e1,e2,...,en}；通过prc分量的完备正交性来追踪原始信号能量与分解能量和之间的差，自适应确定真实的prc分量；

步骤2.3通过kl散度方法来筛选prc分量，各个prc分量与原始信号的kl散度值越大差异性越大，反之越小；

步骤2.4进行hilbert变换求取相位和瞬时频率，根据高频突变点得到扰动起始时刻和扰动终止时刻，由包络函数得到扰动信号4的幅值。

进一步的，所述步骤2.1的具体方法为：

步骤2.1.1确定原信号x(t)的x(t)及对应的时刻t(k)，其中t≥0，k＝1,2,3,...,m,m为极值点个数，并计算基线提取因子l为

其中,

式中k＝1,2,3,...,m-2,0＜α＜1，α是固有旋转分量幅度线性按比例提取的增益控制参数，一般α＝0.5

步骤2.1.2由表达式(1)可知lk的值是从l2到lm-1，两端点l1、lm的值需要估计计算。在两边端点处分别向中间取五个点，根据三次多项式拟合求出两端点l1、lm的值

步骤2.1.3采用三次hermite插值拟合所有的l1,l2,l3,...,,lm，得到基线信号l(t)【3】

步骤2.1.4将基线信号从原信号中分离出来，即

h1(t)＝x(t)-l(t)

若h1(t)满足prc分量的条件，输出h1(t)。否则h1(t)作为原始数据，继续重复上述步骤，直到h1k(t)为prc分量，记prc1＝h1k(t)

步骤2.1.5将prc1分量从原信号中分离出来，则

u1(t)＝x(t)-prc1

得到新的剩余信号u1(t)

步骤2.1.6将u1(t)看作原始数据，重复以上步骤循环n-1次，直到剩余信号un(t)为单调信号或常信号

步骤2.1.7则信号分解为

进一步的，所述步骤2.2的具体方法为：

步骤2.2.1对原始信号求取信号能量

因为xi(t)相互之间是不相关的，即是正交的，有

所以信号x(t)具有的总能量为

式中，ei为x(t)的第i个分量xi(t)的能量

步骤2.2.2当得到的一个prc分量为各分量能量之和为x(t)的正交分量x1(t)，信号的总能量enew与原始信号的能量ex是相等的，当分解的prc分量不是x(t)中的一个正交分量时，信号的总能量enew与原始信号的能量ex有一个误差值为

er＝enew-ex

|er|越小，越能保证信号分解分量的完备正交性，所以当|er|达到最小值时，得到的prc分量是原始信号中的一个正交分量

步骤2.2.3在itd过程中，若能力误差|er|超出允许范围则修正算法。

进一步的，所述步骤2.3的具体方法为：

步骤2.3.1计算原信号x＝{x1，x2，...，xn}与itd分解的第i个prc分量信号yi＝{y1,y2,...,yn}之间的kl散度值，设定该数量级为0.1，则kl散度值大于0.1的prc为无效分量，等于或大于0.1的prc为有效分量；

步骤2.3.2计算两个信号的概率分布，假设x和yi的概率分布分别为y和q(x)，采用非参数估计法求解概率分布，定义核密度函数p(x)为

式中，h为给定的正数，k为高斯核函数：

步骤2.3.3同理得出yi的概率分布q(x)，得出x和yi的kl距离δ(p,q)及δ(q,p)

步骤2.3.4同理得出δ(q,p)，即可得出x和yi的kl散度值

di(p,q)＝δ(p,q)+δ(q,p)

步骤2.3.5设定kl散度值平均值为阈值ε

其中，若某一prc分量kl散度值di(p,q)＜ε，则认为该分量包含了原始信号大部分有用的信息，可作为特征量；反之，若某一prc分量的能量di(p,q)＞ε，则认为该分量包含的原始信号有用信息较少，可将此分量除去。

进一步的，所述步骤2.4的具体方法为：

步骤2.4.1对x(t)进行hilbert变换，则有

可得相应解析函数为

z(t)＝x(t)+jy(t)＝a(t)e^θ(t)

其中相位函数为

瞬时幅值a(t)为

瞬时频率f(t)为

步骤2.4.2：由步骤2.3.1可得对各阶prc分量的幅值进行归一化处理

可得itd信息熵为

式中，pj是第j个prc的幅值分量在总能量中所占的比重

步骤2.4.3从瞬时幅值曲线和瞬时频率曲线获得有效的扰动特征量，所得瞬时频率中可获得扰动期间频率，由瞬时频率曲线两频率突变点对应时刻的差值可得到扰动持续时间，从瞬时幅值可得扰动期间电压成分，所以训练样本的特征量为扰动频率f、扰动幅值a、扰动持续时间t、能量熵he。

进一步的，所述3.2的具体方法为：

步骤3.2.1训练样本数据集中的每个样本x表示为矢量的形式，即

x＝(x1,x2,...,xd)

步骤3.2.2第一个样本矢量被置于输入层单元上，同时，连接输入单元和隐层单元的那些连接被初始化为w1＝x1，然后从隐层的第一个单元到累加层中代表x1所属类别的那个单元之间就建立了一个连接

步骤3.2.3同样的过程对剩余的各个隐层单元都重复进行，即wm＝xm，其中m＝1,2,...,n

步骤3.2.4最后得到训练后的pnn网络，输入层单元和隐层单元之间是万全相通的，而隐层单元到累加层单元之间是稀疏连接的。如果把第j类样本的第k个分量即为xjk，把这个分量到第j个隐层单元的连接权重系数为wjk，其中i＝1,2,...,n，k＝1,2,...,d。

进一步的，所述步骤3.3的具体方法为：

步骤3.3.1把一个测试样本提供给输入节点，每一个隐层单元都计算非线性函数

式中，i＝1,...,m，j＝1,...,n，m为训练样本中总类别数目，ni为第i类训练样本数据数目，d为样本空间数据的维数，σ为平滑参数，xij为第i个模式的第j隐中心矢量

步骤3.3.2每一个累加单元把与它相连的隐层单元的计算fw(x)金子那个相加

步骤3.3.3对每一个累加层单元得到的计算结果，通过求最大值得到测试样本期望的类别，该类别包括：脚步、挖槽、攀爬、车辆过往、自然风、雨。

本发明首先对获取的电容扰动信号进行去噪处理；然后使用固有时间尺度分解算法itd和ht变换提取训练样本特征值；最后构建pnn概率神经网络，将有效的特征量供pnn神经网络训练，经过训练从而调节好pnn概率神经网络的参数，然后将调整好的参数交给概率神经网络分类模块使用；从而具有识别精度高、效率好、灵敏度高、安全性高的优点。

附图说明

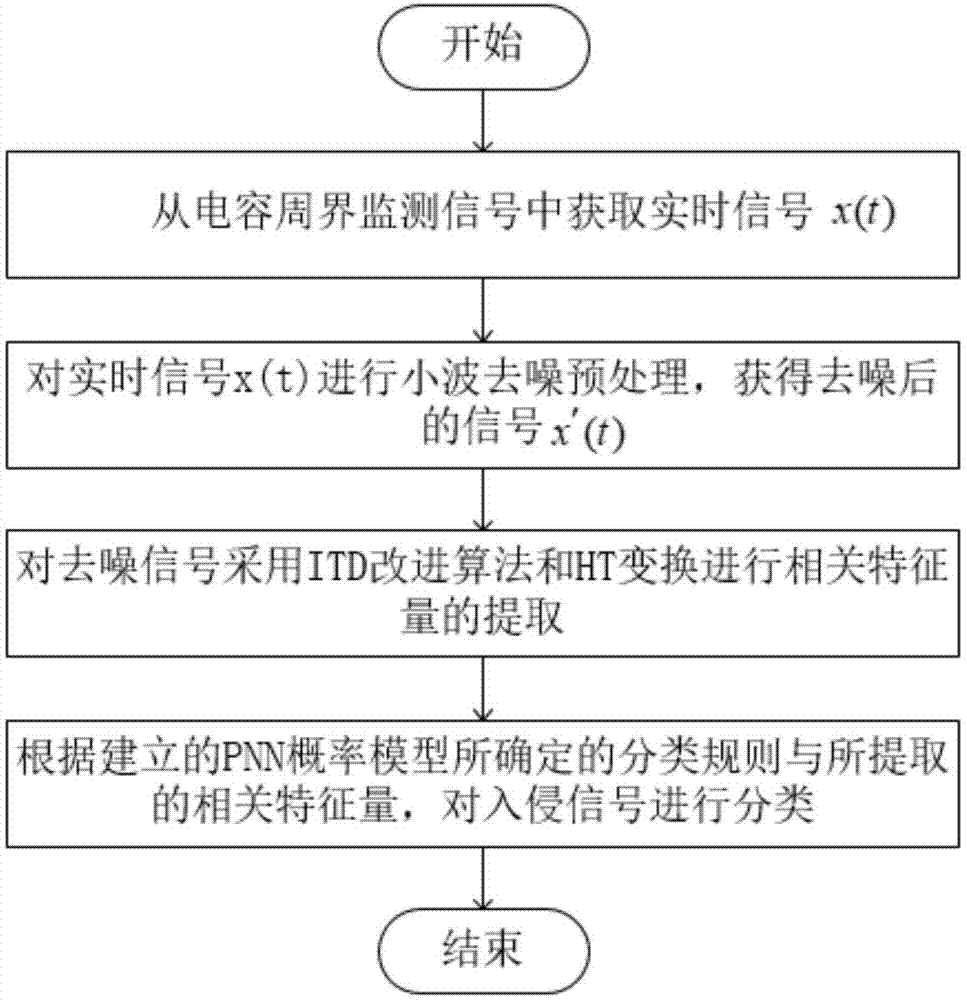
图1为电容扰动周界入侵信号识别方法的流程图；

图2为itd算法改进图；

图3为识别电容周界入侵信号方法的流程图。

具体实施方式

本发明为一种基于电容扰动的周界报警系统入侵信号识别方法，包括以下步骤：

步骤1、对获取的电容扰动信号进行去噪处理；

步骤2、使用固有时间尺度分解算法itd和ht变换提取训练样本特征值；

步骤3、构建pnn概率神经网络，将有效的特征量供pnn神经网络训练，经过训练从而调节好pnn概率神经网络的参数，然后将调整好的参数交给概率神经网络分类模块使用。

进一步的，所述步骤1的具体方法为：

步骤1.1根据电容扰动信号和干扰频带经过实验确定分解层数

步骤1.2选择适当的小波滤波器，对给定的扰动信号进行小波包变换，获得小波包变换系数。常用的正交滤波器包括daubechies小波滤波器、symlets小波滤波器等，经过实验比较选取最佳滤波器

步骤1.3根据原始扰动信号的特点和小波包基函数最佳选取算法，采用自底向顶的方法选取小波基函数

步骤1.4对最佳正交小波包基对应的小波包系数进行处理

步骤1.5重构去除噪声后的扰动信号

进一步的，所述步骤2的具体方法为：

步骤2.1利用固有时间尺度分解算法提取电容扰动信号的固有旋转分量prc和一个残余分量；

步骤2.1.1确定原信号x(t)(t≥0)的x(t)及对应的时刻t(k)(k＝1,2,3,...,m,m为极值点个数)，并计算基线提取因子l为

其中,

式中k＝1,2,3,...,m-2,0＜α＜1，α是固有旋转分量幅度线性按比例提取的增益控制参数，一般α＝0.5

步骤2.1.2由表达式(1)可知lk的值是从l2到lm-1，两端点l1、lm的值需要估计计算。在两边端点处分别向中间取五个点，根据三次多项式拟合求出两端点l1、lm的值

步骤2.1.3采用三次hermite插值拟合所有的l1,l2,l3,...,,lm，得到基线信号l(t)【3】

步骤2.1.4将基线信号从原信号中分离出来，即

h1(t)＝x(t)-l(t)

若h1(t)满足prc分量的条件，输出h1(t)。否则h1(t)作为原始数据，继续重复上述步骤，直到h1k(t)为prc分量，记prc1＝h1k(t)

步骤2.1.5将prc1分量从原信号中分离出来，则

u1(t)＝x(t)-prc1

得到新的剩余信号u1(t)

步骤2.1.6将u1(t)看作原始数据，重复以上步骤循环n-1次，直到剩余信号un(t)为单调信号或常信号

步骤2.1.7则信号分解为

步骤2.2经itd分解得到的n个prc分量，每个分量都包含有其各自的频率成分f1,f2,...,fn，其中含有不同的能量e＝{e1,e2,...,en}。通过prc分量的完备正交性来追踪原始信号能量与分解能量和之间的差^【4】，自适应确定真实的prc分量；

步骤2.2.1对原始信号求取信号能量

因为xi(t)相互之间是不相关的，即是正交的，有

所以信号x(t)具有的总能量为

式中，ei为x(t)的第i个分量xi(t)的能量

步骤2.2.2当得到的一个prc分量为各分量能量之和为x(t)的正交分量x1(t)，信号的总能量enew与原始信号的能量ex是相等的，当分解的prc分量不是x(t)中的一个正交分量时，信号的总能量enew与原始信号的能量ex有一个误差值为

er＝enew-ex

|er|越小，越能保证信号分解分量的完备正交性，所以当|er|达到最小值时，得到的prc分量是原始信号中的一个正交分量

步骤2.2.3在itd过程中，若能力误差|er|超出允许范围则修正算法

步骤2.3通过kl散度方法来筛选prc分量，各个prc分量与原始信号的kl散度值越大差异性越大，反之越小。

步骤2.3.1计算原信号x＝{x1，x2，...，xn}与itd分解的第i个prc分量信号yi＝{y1,y2,...,yn}之间的kl散度值，设定该数量级为0.1，则kl散度值大于0.1的prc为无效分量，等于或大于0.1的prc为有效分量。

步骤2.3.2计算两个信号的概率分布，假设x和yi的概率分布分别为y和q(x)，采用非参数估计法求解概率分布，定义核密度函数p(x)为

式中，h为给定的正数，k为高斯核函数：

步骤2.3.3同理得出yi的概率分布q(x)，得出x和yi的kl距离δ(p,q)及δ(q,p)

步骤2.3.4同理得出δ(q,p)，即可得出x和yi的kl散度值

di(p,q)＝δ(p,q)+δ(q,p)

步骤2.3.5设定kl散度值平均值为阈值ε

其中，若某一prc分量kl散度值di(p,q)＜ε，则认为该分量包含了原始信号大部分有用的信息，可作为特征量；反之，若某一prc分量的能量di(p,q)＞ε，则认为该分量包含的原始信号有用信息较少，可将此分量除去

步骤2.4进行hilbert变换求取相位和瞬时频率，根据高频突变点得到扰动起始时刻和扰动终止时刻，由包络函数得到扰动信号4的幅值

步骤2.4.1对x(t)进行hilbert变换，则有

可得相应解析函数为

z(t)＝x(t)+jy(t)＝a(t)e^θ(t)

其中相位函数为

瞬时幅值a(t)为

瞬时频率f(t)为

步骤2.4.2：由步骤2.3.1可得对各阶prc分量的幅值进行归一化处理

可得itd信息熵为

式中，pj是第j个prc的幅值分量在总能量中所占的比重

步骤2.4.3从瞬时幅值曲线和瞬时频率曲线获得有效的扰动特征量，所得瞬时频率中可获得扰动期间频率，由瞬时频率曲线两频率突变点对应时刻的差值可得到扰动持续时间，从瞬时幅值可得扰动期间电压成分，所以训练样本的特征量为扰动频率f、扰动幅值a、扰动持续时间t、能量熵he

进一步的，所述步骤3的具体方法为：

步骤3.1对输入矩阵进行归一化处理，训练样本的最终特征向量矩阵为

x＝[f,a,t,he]

步骤3.2pnn训练步骤

步骤3.2.1训练样本数据集中的每个样本x表示为矢量的形式，即

x＝(x1,x2,...,xd)

步骤3.2.2第一个样本矢量被置于输入层单元上，同时，连接输入单元和隐层单元的那些连接被初始化为w1＝x1，然后从隐层的第一个单元到累加层中代表x1所属类别的那个单元之间就建立了一个连接

步骤3.2.3同样的过程对剩余的各个隐层单元都重复进行，即wm＝xm，其中m＝1,2,...,n

步骤3.2.4最后得到训练后的pnn网络，输入层单元和隐层单元之间是万全相通的，而隐层单元到累加层单元之间是稀疏连接的。如果把第j类样本的第k个分量即为xjk，把这个分量到第j个隐层单元的连接权重系数为wjk，其中i＝1,2,...,n，k＝1,2,...,d

步骤3.3pnn分类识别步骤

步骤3.3.1把一个测试样本提供给输入节点，每一个隐层单元都计算非线性函数

式中，i＝1,...,m，j＝1,...,n，m为训练样本中总类别数目，ni为第i类训练样本数据数目，d为样本空间数据的维数，σ为平滑参数，xij为第i个模式的第j隐中心矢量

步骤3.3.2每一个累加单元把与它相连的隐层单元的计算fw(x)金子那个相加

步骤3.3.3对每一个累加层单元得到的计算结果，通过求最大值得到测试样本期望的类别(脚步、挖槽、攀爬、车辆过往、自然风、雨)。