一种高速公路瓶颈区域自动驾驶协同控制方法

1.本发明涉及自动驾驶控制领域，具体涉及一种高速公路瓶颈区域自动驾驶协同控制方法。


背景技术：

2.得益于全球新一轮科技革命和产业变革蓬勃发展，电动化、网联化、智能化成为汽车产业的发展潮流和趋势，国家也相继出台了相关政策支持自动驾驶汽车的发展。目前，在车辆智能化的研究及应用领域，已经取卓有成效的成果，如何在单车智能化基础上实现协同驾驶，探索多车间的协作机制，研究多车协同的行为决策方法，对于提高交通安全，缓解交通拥堵的智能交通系统具有重要意义。
3.瓶颈区域是指路网中易发生交通拥堵的路段，同时也是路网中的薄弱路段，是影响整个路网水平的关键路段。交通网络中造成瓶颈的原因主要有日益增长的道路交通需求、道路条件不合理、交通流状态与突发事件等。而高速公路瓶颈区域主要是指由于突发事故、道路施工、车辆行驶过程中的分流合流现象导致该路段的通行能力降低，引发交通拥堵。
4.协作驾驶的一个关键点是确定控制区域内的车辆在瓶颈区域的通行权(通行顺序)。协作驾驶中确定通行顺序的策略可大致分为两类，基于临时协商的和基于计划的。基于临时协商的方法，大多数是通过基于先进先出的通行优先权顺序来协调车辆轨迹，能够非常短的时间内求解出来，但是基于先进先出的通行优先权顺序不是解决该问题的通解，在大多数情况下，还存在比该顺序更好的解，或者有个别情况是该顺序不能解决的。基于规划的策略，它考虑将在瓶颈区域的某个空间范围内到达的车辆，并为车辆制定相对长期的驾驶计划，通过数学规划或者启发式算法(蚁群算法、遗传算法等)来直接求解该模型，然而该过程要花费大量时间，特别是在考虑车辆避碰问题上。基于临时协商和规划的方法大多数没有考虑车辆变道情况，近几年也出现了新研究考虑了车辆变道情况，将基于轨迹的交通管理问题表述为混合整数规划问题，并且开发了基于滚动时域方法来提高计算效率，为多辆自动驾驶车辆寻找最佳轨迹以及解决冲突问题，然而该方法将变道机动假设为在给定时间内完成，忽略了变道过程中的突发情况。以上方法大多数仅仅是将通行时间最小化作为优化目标，没有考虑能耗问题。


技术实现要素：

5.本发明主要面向全自动驾驶车辆的复杂驾驶场景例如车道数减少或者道路有瓶颈区域驾驶场景，提供一种高速公路瓶颈区域自动驾驶协同优化方法。
6.为了实现上述任务，本发明采用以下技术方案：
7.一种高速公路瓶颈区域自动驾驶协同优化方法，包括以下步骤：
8.设定针对于高速公路瓶颈区域的控制区域，对于控制区域内的车辆，构建考虑车辆通行时间、耗电量的车辆轨迹优化模型；所述模型用于根据车辆的实时速度、加速度来计
算成本值；
9.将车辆的通行优先权顺序寻优转换为树搜索以进行树结构的展开，将蒙特卡洛树搜索算法与设定的选择策略相结合，使得搜索不断向总成本更小的方向进行搜索，得到候选的通行优先权顺序；
10.根据所述候选通行优先权顺序对车辆轨迹进行轨迹规划，使得车辆能从初始化状态行驶到候选的通行优先权顺序所对应的状态；
11.通过不断循环迭代，直到所述树结构扩展的节点中包含所有车辆为止，得到对应总成本最小的通行优先权顺序和对应的车辆轨迹，然后利用该车辆轨迹对控制范围内的车辆进行控制，达到最小化通行时间和耗电量的目的。
12.进一步地，所述车辆轨迹优化模型表示如下：
[0013][0014]
其中，x(t),u(t)分别为控制区域内车辆在t时刻的状态集合和输入向量集合，n为控制区域内的车辆数，ω1、ω2分别为时间成本系数和耗电成本系数，用于将成本转换为价格；和分别表示车辆i通过瓶颈区域的时间和进入瓶颈区域的时间，表示车辆i的净耗电量，由车辆的运动学数据、车辆的系统间转换效率计算得到；
[0015]
所述车辆轨迹优化模型的约束包括车辆动力学约束、车辆的通行优先权以及车辆碰撞避免约束。
[0016]
进一步地，所述将车辆的通行优先权顺序寻优转换为树搜索以进行树结构的展开，将蒙特卡洛树搜索算法与设定的选择策略相结合，包括：
[0017]
3.1对控制区域内的车辆进行id分配；
[0018]
3.2将每个车辆作为一个节点，节点的数据信息包含车辆编号id组成的字符串s、父节点和子节点信息，并且包含其被遍历次数n、奖励值q；
[0019]
3.3传入当前需要开始搜索的起始节点p，根据设定的选择策略返回最好的节点进行扩展，如果节点是叶节点，此时全部车辆编号id均在字符串s中，则直接结束；
[0020]
3.4对于所返回的节点，该节点上拓展一个新节点作为其子节点，其中新节点的字符串s形成是在其父节点的字符串的末尾添加新的车辆编号id；在此过程中，对于同一父节点的子节点，它们之间的字符串s不能重复；
[0021]
3.5对于所述新节点进行奖励值评估，在此过程中进行节点的通行优先权顺序规划，并计算该新节点的奖励值；
[0022]
3.6根据所述新节点的奖励值，向上回溯，对该新节点及其上游父节点的数据信息进行更新；
[0023]
3.7重复步骤3.3
‑
3.7，直到循环起始节点中的字符串s包含了所有的车辆编号id，则该字符串s为最优的候选通行优先权顺序。
[0024]
进一步地，所述对于所述新节点进行奖励值评估，在此过程中进行节点的通行优先权顺序规划，并计算该新节点的奖励值，包括：
[0025]
3.5.1根据给出的新节点，获取该节点的字符串s，若s包含所有的车辆编号id，则直接跳过步骤3.5.2，否则需要将未添加的车辆编号id追加到s中，进而得到完整的通行优
先权顺序ψ，具体步骤如下：
[0026]
(1)首先将车辆编号按照车道分成三个数组p1、p2、p3，数组内元素按照距离冲突区域纵向距离排序；
[0027]
(2)将p1、p2、p3中已经出现在字符串s中的元素移除，若出现空数组则也将其移除；在所存数组中随机选择一个数组p
i
，并取出其第一个元素p
i
(1)，将该元素添加到s的末尾；
[0028]
(3)重复步骤(1)和(2)，直到s中包含所有车辆id；最后得到完整通行优先权顺序ψ；
[0029]
3.5.2将步骤3.5.1给出的完整的通行优先权顺序ψ进行车辆轨迹规划，最后得到新节点的奖励值。
[0030]
进一步地，所述设定的选择策略为：
[0031]
先找当前未遍历过的子节点，如果有多个则随机选；如果都遍历过就找ucb值最大的，如果ucb值相等则随机选；节点v
′
的ucb值计算如下：
[0032][0033]
其中，v
′
表示当前节点，v表示v
′
的父节点，q表示该节点的累计的奖励值，n表示节点的访问次数，c为权重参数。
[0034]
进一步地，根据所述候选通行优先权顺序对车辆轨迹进行轨迹规划，使得车辆能从初始化状态行驶到候选的通行优先权顺序所对应的状态，包括：
[0035]
4.1将所有车辆id构建矩阵，将其与候选通行优先权顺序矩阵进行差分运算，并对该结果进行处理，使得差分值对应的车辆id与其索引值一致，最后得到差分矩阵，进而确定车辆的目标速度；
[0036]
4.2根据所确定的目标速度，进行单辆车辆的轨迹规划；
[0037]
4.3局部轨迹规划：将控制区域内所有的车辆都执行步骤4.2，即可得到所有车辆的局部轨迹优化；
[0038]
4.4全局轨迹规划：根据步骤4.3所得到的所有车辆的局部轨迹，为得到全局轨迹，需要不断地进行采样更新车辆位置信息，然后根据车辆更新的位置信息重新进行执行步骤4.3中的局部轨迹规划；
[0039]
4.5循环执行步骤4.4直到所有车辆均通过瓶颈区域为止；最后得到车辆整个过程的轨迹规划方案、总通行时间和总耗电量，然后计算出该过程的总成本值；
[0040]
4.6根据步骤4.5所得到的总成本值，将其反馈回到步骤3.5.2中作为其奖励值q。
[0041]
进一步地，根据所确定的目标速度，进行单辆车辆的轨迹规划，包括：
[0042]
4.2.1在frenet坐标中根据沿着给定参考线的纵向位移s和距离该参考线的横向偏移d来指定车辆位置(s,d)，同时轨迹点可以用来表示，其中分别为s的一阶导和二阶导，分别为d的一阶导和二阶导；
[0043]
4.2.2，定义车辆轨迹集合集合中的轨迹都是由s(t)和d(t)构成，表示为沿着frenet轴的时间多项式：
[0044][0045]
其中，s(t)和d(t)表示t时刻的纵向位移s、横向偏移d，a
i
、c
i
为多项式系数，t
i
为时间参数，t0为轨迹起始时间，t
f
为轨迹终点时间；故若要求出完整的轨迹集合则只需要求解出a
i
、c
i
这些多项式系数即可；
[0046]
4.2.3，在得到frenet坐标下的轨迹集合后，经过数值变换将其转换为笛卡尔坐标[x,y,θ,k,v,a]，其中[x,y]为在笛卡尔坐标系下位置，k为曲率，θ为航向角，v为速度，a为加速度；
[0047]
4.2.4，根据车辆的动力学约束和车辆碰撞避免约束，可以将其细化为硬约束和软约束，用以排除不符合约束条件的轨迹以及挑选出最优轨迹
[0048]
进一步地，求解多项式系数a
i
、c
i
以得到完整的轨迹集合的过程为：
[0049]
(1)为了保持前一轨迹的连续性和动态可行性，需要对轨迹终端的做出以下约束：
[0050][0051]
其中，t
f
为轨迹终点时间；d
f
为最终横向位置，忽略了终端状态的横向速度，所以d在终点时间的导数及二阶导均设为0；v
f
为最终纵向速度；
[0052]
(2)可以通过确定的轨迹初始状态和轨迹末端状态并在时间间隔t内，利用五次和四次多项式来进行拟合求解出a
i
、c
i
，进而完成这两个状态之间的轨迹规划；
[0053]
(3)为得到d
f
、v
f
的取值，分别设置三种不同的终止状态，即巡航、变道和跟车模式，具体设置如下：
[0054]
a)巡航模式下，设置d
f
保持与初始状态的d0一样，v
f
设置为目标速度；
[0055]
b)变道模式下，设置d
f
为邻近车道中心，v
f
设置为目标速度；
[0056]
c)跟车模式下，设置d
f
保持与初始状态的d0一样，v
f
设置为前车速度。
[0057]
(4)通过以上步骤可以得到一个轨迹集合
[0058]
进一步地，所述根据车辆的动力学约束和车辆碰撞避免约束，可以将其细化为硬约束和软约束，用以排除不符合约束条件的轨迹以及挑选出最优轨迹包括：
[0059]
a)碰撞避免约束，若轨迹集合中存在与其他车辆发生碰撞的轨迹则直接排除该碰撞轨迹
[0060]
b)硬约束，用以排除不符合车辆动力性能标准的轨迹：
[0061][0062]
上式中，k(t)、θ(t)、a(t)表示t时刻的曲率k、航向角θ、加速度a；k
max
、θ
max
、v
max
、a
max
表示设定的曲率、航向角、速度、加速度的最大值，v
min
表示设定的速度最小值；
[0063]
c)软约束，通过设计一个成本函数，然后利用数值优化在轨迹集中找出成本最小的轨迹；
[0064][0065]
其中，表示轨迹集，ω
d
、ω
v
、ω
a
为权重系数，d
des
表示目标车道中心，c
des
(t)表示标速度，a(t)表示车辆加速度，d(t)和v(t)表示t时刻的横向偏移和速度；
[0066]
d)通过步骤a)、b)、c)的筛选，可以在轨迹集合中挑选最优的轨迹
[0067]
与现有技术相比，本发明具有以下技术特点：
[0068]
1.在优化函数中不仅考虑了通行时间成本，而且还考虑了耗电成本，并通过权重系数将这两者转换为价格成本来进行优化。
[0069]
2.在通行优先权顺序寻优部分，把通行优先权顺序转换为树搜索，利用蒙特卡洛树搜索算法来进行求解，同时结合所提出的设定的选择策略，加快了最优通行顺序的搜索，同时确保了结果的性能。
[0070]
3.在车辆轨迹规划部分，提出一个动态轨迹规划方法来解决轨迹规划。在frenet坐标下进行轨迹规划，通过不断迭代局部轨迹规划算法，进而得到整个变化过程的轨迹规划。该过程中考虑了车辆变道机动的变化过程；通过车辆间动态决策轨迹规划来避免多车轨迹规划陷入局部最优解，同时也加快了轨迹规划的过程。
[0071]
4.提出双层闭环求解框架，将高速公路瓶颈区域的通行优化问题，拆分为两个部分(通行优先权寻优和车辆轨迹规划)，第一层通过结合蒙特卡洛树搜索方法来进行通行优先权寻优，第二层则在第一层基础上进行车辆轨迹动态规划，降低了求解复杂度，通过蒙特卡洛树搜索方法与车辆轨迹动态规划方法两个部分不断循环迭代，最后得到最优通行优先权顺序和车辆轨迹规划方案，加快了求解速度，同时保证所得的结果在减少通行时间和减少能耗方面有很好的表现。
附图说明
[0072]
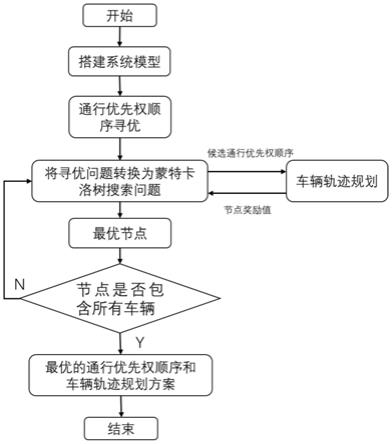
图1为本发明一个实施例中控制方法的流程示意图；
[0073]
图2为驾驶场景示意图；
[0074]
图3为闭环求解框架示意图；
[0075]
图4为蒙特卡洛树搜索算法迭代过程图；
[0076]
图5为轨迹生成示意图。
具体实施方式
[0077]
本发明主要面向全自动驾驶车辆的复杂驾驶场景例如车道数减少或者道路有瓶颈区域驾驶场景，如图2所示。对于图2所示驾驶场景中的车辆是均采用自动驾驶模式的，并且在v2x通信技术的支持下，可以与相邻车辆和道路基础设施共享其驾驶状态(位置、速度、加速度等)和意图，以更好地协调其运动。因此，我们可以将高速公路瓶颈区域的协作驾驶问题表述为轨迹规划问题，约束包括车辆动力学、安全性、物理约束和通行优先权顺序。
[0078]
参见附图，本发明提出的一种高速公路瓶颈区域自动驾驶协同控制方法，该方法建立的优化模型考虑了通行效率和能耗方面，以最小化通行时间和耗电量为优化目标，克服现有优化方法未兼顾能耗的问题。为求解该模型，通过一个双层闭环求解框架，第一层通过结合蒙特卡洛树搜索方法来进行通行优先权寻优，第二层则在第一层基础上进行车辆轨
迹动态规划，通过不断循环迭代，最后得到最优通行优先权顺序和车辆轨迹规划方案，进而解决该优化问题。本方法包括以下步骤：
[0079]
步骤1，设定针对于高速公路瓶颈区域的控制区域，对于控制区域内的车辆，构建考虑车辆通行时间、耗电量的车辆轨迹优化模型；所述模型用于根据车辆的实时速度、加速度来计算成本值。
[0080]
该步骤中，对于高速公路瓶颈区域设定控制区域，对控制区域中的所有车辆，建立轨迹优化模型；所述瓶颈区域是指公路上因车祸、施工、自然灾害等造成的部分车道不能通行的情况。控制区域的大小根据实际需求设定，例如本实施例中控制区域为距离高速公路瓶颈区域500米的路段。
[0081]
1.1根据车辆的物理及设计约束，对于控制区域范围内的n台车辆，建立车辆动力学约束：
[0082][0083]
其中，x
i
(t)表示车辆i在t时刻的状态，即车辆当前位置和速度所组成的向量值；u
i
(t)表示车辆i在t时刻的输入向量，即车辆速度和加速度组成的输入向量；为x
i
(t)的时间导数；f
i
(
·
)函数表示的是车辆的动力学约束。
[0084]
1.2设置车辆i的通行优先权p
i
∈p，其中p为控制区域内所有车辆的通行优先权矩阵，当两车存在潜在冲突风险时，优先权低的车辆要进行减速避让优先权高的车辆。
[0085]
1.3设置车辆碰撞避免约束，用g
i
(x
i
(t),p
i
)来表示车辆i在状态为x
i
(t)时所占有的空间范围；因此，车辆i和j在t时刻没有产生冲突的情况可表示为：
[0086][0087]
其中，p
i
和p
j
表示车辆i和j的通行优先权。
[0088]
1.4使用行驶过程中时间成本和耗电成本构建目标函数，以便于优化后的模型可以在时间成本和耗电成本之间有个很好的均衡：
[0089][0090]
其中，j
i
(
·
)表示车辆i的成本函数；和分别表示车辆i通过瓶颈区域的时间和进入瓶颈区域的时间；ω1、ω2分别为时间成本系数和耗电成本系数，以便于将成本转换为价格；本实施例中，取值分别为0.01和0.8；表示车辆i的净耗电量。
[0091]
对于以每秒的车速和加速度作为输入来计算车辆的瞬时耗电量；净耗电量具体计算过程如下：
[0092]
1.4.1根据车辆运动学数据(例如瞬时速度、加速度)、道路坡度、滚动摩擦和车辆特性等来计算车轮处瞬时功率p
w
(t)；然后，基于车辆系统间转换效率(即发动机、制动系统、电池)来计算瞬时所需牵引功率p
t
(t)或产生的再生功率p
r
(t)；最后，在车辆行驶期间，对p
t
(t)和p
r
(t)进行积分运算，进而可以得到该驾驶过程中能量消耗和能量回收，并由此得到车辆在行驶过程中的净耗电量e
ac
。
[0093]
1.4.2车轮处瞬时功率p
w
(t)计算如下：
[0094]
[0095]
其中，m为车辆质量；a(t)为车辆在t时刻的瞬时加速度；v(t)为车辆在t时刻的瞬时速度；g为重力加速度，取值为9.8066m/s2；θ为道路坡度；c
r
、c1和c2为滚动阻力参数，其与路面类型、路况以及车辆轮胎有关；ρ
air
为空气质量密度，在海平面温度为15℃时，其取值为1.2256kg/m3；a
f
为车辆前部区域面积大小；c
d
为车辆空气动力阻力系数。
[0096]
1.4.3当车辆处于牵引模式时，能量从电机流向车轮。此时，电动机的功率高于车轮的功率，并且假设车轮的功率为正；当车辆处于再生制动模式下，能量从车轮流向电机。此时，电动机的功率低于车轮的功率，并且功率被假定为负。故p
t
(t)和p
r
(t)可以根据p
w
(t)的值来进行计算：
[0097][0098]
其中，η
dl
为传动系统的转换效率；η
em
为电动机的转换效率；η
bat
为电池系统的转换效率；η
rb
(t)为再生制动系统转换效率，其与瞬时加速度有关，定义如下：
[0099][0100]
其中，a的值取决于电动车辆的特性，通常在[0,1]之间取值，e为自然对数底数。
[0101]
1.4.4结合以上公式，可以直接求取能耗e
c
以及能量回收e
r
：
[0102][0103][0104]
其中，t0和t
e
分别表示计算周期的起始时间和终止时间。
[0105]
1.4.5最后，车辆在行驶过程中的净耗电量e
ac
可以用下式得出：
[0106]
e
ac
＝e
c
‑
e
r
[0107]
1.5结合以上步骤，可以得到完整的车辆轨迹优化模型(成本函数)，通过最小化该模型的成本值，即可解决高速公路瓶颈区域的车辆协同控制问题。
[0108][0109]
其中，x(t),u(t)分别为控制区域内车辆在t时刻的状态集合和输入向量集合。
[0110]
步骤2，将车辆的通行优先权顺序寻优转换为树搜索以进行树结构的展开，将蒙特卡洛树搜索算法与设定的选择策略相结合，使得搜索不断向总成本更小的方向进行搜索，得到候选的通行优先权顺序。
[0111]
针对所述车辆轨迹优化模型，直接求解将会是一个很难解决的混合整数规划问题，尤其是在考虑车辆间避碰以及变道问题上。为此通过一个双层闭环求解框架来进行求解，如图3所示。其中第一层通过结合蒙特卡洛树搜索方法来进行通行优先权寻优，解决步骤1.2中的通行优先权的寻优问题；第二层则在第一层基础上进行车辆轨迹动态规划，解决步骤1.1、1.3和1.4中的规划问题；通过不断循环迭代，最后得到最优通行优先权顺序和车
辆轨迹规划方案，进而解决高速公路瓶颈区域的车辆协同控制问题，即解决步骤1.5所提出的完整车辆轨迹优化模型。具体步骤如步骤3和步骤4。
[0112]
步骤3，结合蒙特卡洛树搜索方法来进行通行优先权寻优
[0113]
针对步骤1.2的通行优先权的寻优问题，将其中的通行优先权寻优问题转化为树搜索问题，利用蒙特卡洛树搜索方法和设定的选择策略来进行求解。以车辆编号id组成的字符串作为每个节点来进行展开。其中，在展开的树结构中最上层的优先权最高，最底层的优先权最低。例如，“2
‑3‑
1”节点中，2号车辆优先权最高，其将率先通过瓶颈区域，并且当其与其他车辆发生冲突时，其他车辆要进行避让。树结构搜索示意图如图4所示，具体过程如下：
[0114]
3.1对控制区域内的车辆进行id分配(按照车辆进入控制范围内的时间顺序进行编号，最早进入的车辆id为1；若进入时间相同则根据前进方向的所在的车道从左到右顺序进行id分配)。
[0115]
3.2将每个车辆作为一个节点，节点的数据信息包含车辆编号id组成的字符串s、父节点和子节点信息，并且包含其被遍历次数n、奖励值q；
[0116]
3.3选择阶段：传入当前需要开始搜索的起始节点p(例如根节点)，根据设定的选择策略返回最好的节点进行扩展(步骤3.4)，如果节点是叶节点(即全部车辆编号id均在字符串s中)则直接结束。
[0117]
本方案中选择策略是先找当前未遍历过的子节点，如果有多个则随机选；如果都遍历过就找ucb值最大的，如果ucb值相等则随机选。节点v
′
的ucb值计算如下：
[0118][0119]
其中，v
′
表示当前节点，v表示v
′
的父节点，q表示该节点的累计的奖励值，n表示节点的访问次数，为权重参数；该公式前半部分用于利用，鼓励选择当前最优子节点；后半部分用于探索，鼓励探索更多的子节点。
[0120]
3.4扩展阶段：输入3.3中给出的节点，在该节点上拓展一个新节点作为其子节点，其中新节点的字符串s形成是在其父节点的字符串的末尾添加新的车辆编号id；最后将该新拓展的节点传给步骤3.5。
[0121]
该过程需要保证所新组成的字符串s中不能出现同一车道上的车，前车优先权比后车优先权低(通过此限制条件可以限定节点拓展的子节点数量)；对于同一父节点的子节点，它们之间的字符串s不能重复。
[0122]
3.5仿真阶段：根据步骤3.4给出的新节点，进行奖励值评估，具体过程如下：
[0123]
3.5.1根据给出的新节点，获取该节点的字符串s，若s包含所有的车辆编号id(即得到完整的通行优先权顺序ψ)，则直接跳过步骤3.5.2，否则需要将未添加的车辆编号id追加到s中，进而得到完整的通行优先权顺序ψ：
[0124]
该步骤中将字符串s作为输入，输出完整的通行优先权顺序，具体步骤如下：
[0125]
(1)首先将车辆编号按照车道分成三个数组p1、p2、p3，数组内元素按照距离冲突区域纵向距离排序(从小到大)；
[0126]
(2)将p1、p2、p3中已经出现在字符串s中的元素移除，若出现空数组则也将其移除；
在所存数组中随机选择一个数组p
i
，并取出其第一个元素p
i
(1)，将该元素添加到s的末尾；
[0127]
(3)重复步骤(1)—(2)，直到s中包含所有车辆id；最后得到完整通行优先权顺序ψ；
[0128]
3.5.2将步骤3.5.1给出的完整的通行优先权顺序ψ传递给步骤4中进行车辆轨迹规划，最后得到一个奖励值(即为该新节点的奖励值q)。
[0129]
3.6回溯阶段：根据步骤3.5中得到的奖励值q，进行向上回溯，对该新节点及其上游父节点的数据信息(奖励值q和被遍历次数n)进行更新，即q＝q+q、n＝n+1。
[0130]
3.7通过在有限时间内，循环执行步骤3.3
‑
3.6，之后根据不断更新的数据信息，再通过步骤3.3中的选择策略，选择出节点p的最优子节点作为下一轮的循环起始节点，重复步骤3.3
‑
3.7，直到循环起始节点中的字符串s包含了所有的车辆编号id，则该字符串s为最优的候选通行优先权顺序。
[0131]
步骤4，根据所述候选通行优先权顺序对车辆轨迹进行轨迹规划，使得车辆能从初始化状态行驶到候选的通行优先权顺序所对应的状态。
[0132]
该步骤中，利用步骤3中给定的候选通行优先权顺序ψ，对控制区域内的车辆进行轨迹规划：首先，先解决单辆车的轨迹规划，并将其扩展到多辆车中，得到所有车辆的局部轨迹，然后通过不断迭代局部轨迹规划算法，进而得到整个变化过程的轨迹规划，同时根据步骤1.4计算出所有车辆在整个过程的总成本值(即奖励值q)。具体步骤如下：
[0133]
4.1，将步骤3.1的车辆id构建矩阵v，将其与通行优先权顺序矩阵ψ进行差分运算，并对该结果进行处理，使得差分值对应的车辆id与其索引值一致，最后得到差分矩阵d(差分值大于0的则表示需要加速，等于0的表示匀速，小于0表示减速)，进而确定车辆的目标速度target_v。
[0134]
4.2，根据步骤4.1所确定的车辆目标速度target_v，进行车辆轨迹规划(单辆车辆)。具体过程如下：
[0135]
4.2.1，该车辆轨迹规划方法是在frenet坐标系下进行的。在frenet坐标中根据沿着给定参考线(一般定义为道路中心线)弧线的纵向位移s和距离该参考线的横向偏移d来指定车辆位置(s,d)，同时轨迹点可以用来表示，其中分别为s的一阶导和二阶导，分别为d的一阶导和二阶导。
[0136]
4.2.2，定义车辆轨迹集合这些轨迹都是由s(t)和d(t)构成，可以表示为沿着frenet轴的时间多项式：
[0137][0138]
其中，s(t)和d(t)表示t时刻的纵向位移s、横向偏移d，a
i
、c
i
为多项式系数，k＝4，r＝5，t
i
为时间参数，t0为轨迹起始时间，t
f
为轨迹终点时间；故若要求出完整的轨迹集合则只需要求解出a
i
、c
i
这些多项式系数即可，具体过程如下：
[0139]
(1)为了保持前一轨迹的连续性和动态可行性，需要对轨迹终端的做出以下约束：
[0140][0141]
其中，t
f
为轨迹终点时间；d
f
为最终横向位置，忽略了终端状态的横向速度，所以d在终点时间的导数及二阶导均设为0；v
f
为最终纵向速度。
[0142]
(2)可以通过确定的轨迹初始状态和轨迹末端状态并在时间间隔t内，利用五次和四次多项式来进行拟合(即求解出a
i
、c
i
)，进而完成这两个状态之间的轨迹规划；结合(1)中所给出的约束，由于初始状态和终点时间已知，故关键在于确定终止状态中d
f
、v
f
。所以通过改变这两个参数，则可以得到一个轨迹集合
[0143]
其中，s0、d0为初始状态时的纵向位移s、横向偏移d。
[0144]
(3)为得到d
f
、v
f
的取值，我们分别设置三种不同的终止状态，即巡航、变道和跟车模式，具体设置如下：
[0145]
a)巡航模式下，设置d
f
保持与初始状态的d0一样，v
f
设置为目标速度target_v；
[0146]
b)变道模式下，设置d
f
为邻近车道中心，v
f
设置为目标速度target_v；
[0147]
c)跟车模式下，设置d
f
保持与初始状态的d0一样，v
f
设置为前车速度。
[0148]
(4)通过以上步骤可以得到一个轨迹集合生成轨迹如图5所示。
[0149]
4.2.3，在得到frenet坐标下的轨迹集合后，经过数值变换将其转换为笛卡尔坐标[x,y,θ,k,v,a]，其中[x,y]为在笛卡尔坐标系下位置，k为曲率，θ为航向角，v为速度，a为加速度，以便于消除不可行的轨迹以及选择最优轨迹。
[0150]
4.2.4，根据步骤1.1所建立的动力学约束和步骤1.3车辆碰撞避免约束，可以将其细化为硬约束和软约束，用以排除不符合约束条件的轨迹以及挑选出最优轨迹具体如下：
[0151]
a)碰撞避免约束，若轨迹集合中存在与其他车辆发生碰撞的轨迹则直接排除该碰撞轨迹
[0152]
b)硬约束，用以排除不符合车辆动力性能标准的轨迹，主要是使得曲率k，航向角θ，速度v以及加速度a在控制范围内：
[0153][0154]
上式中，k(t)、θ(t)、a(t)表示t时刻的曲率k、航向角θ、加速度a；k
max
、θ
max
、v
max
、a
max
表示设定的曲率、航向角、速度、加速度的最大值，v
min
表示设定的速度最小值。
[0155]
c)软约束，主要考虑安全性、可靠性和舒适性等方面，通过设计一个成本函数，然后利用数值优化在轨迹集中找出成本最小的轨迹；
[0156][0157]
其中，表示轨迹集，ω
d
、ω
v
、ω
a
为权重系数，第一项j0表示最小化车辆到目标车道中心d
des
的横向偏移，以确保安全性；第二项j
v
表示车辆尽量要以目标速度行驶v
des
(t)，以确保可靠性；第三项j
a
表示车辆加速度a(t)变化，以确保舒适性。d(t)和v(t)表示t时刻的横向偏移和速度。
[0158]
d)通过步骤a)、b)、c)的筛选，可以在轨迹集合中挑选最优的轨迹
[0159]
4.3，局部轨迹规划：将控制区域内所有的车辆都执行步骤4.2，即可得到所有车辆
的局部轨迹优化；
[0160]
4.4，全局轨迹规划：根据步骤4.3所得到的所有车辆的局部轨迹，为得到全局轨迹，需要不断地进行采样更新车辆位置信息，然后根据车辆更新的位置信息重新进行执行步骤4.3中的局部轨迹规划。
[0161]
4.5，循环执行步骤4.4直到所有车辆均通过瓶颈区域为止；最后得到车辆整个过程的轨迹规划方案、总通行时间和总耗电量，然后根据步骤1.5来计算出该过程的总成本值；
[0162]
4.6，根据步骤4.5所得到的总成本值，将其反馈回到步骤3.5.2中作为其奖励值q。
[0163]
步骤5，通过不断循环迭代，直到所述树结构扩展的节点中包含所有车辆为止，得到对应总成本最小的通行优先权顺序和对应的车辆轨迹，然后利用该车辆轨迹对控制范围内的车辆进行控制，达到最小化通行时间和耗电量的目的。
[0164]
利用步骤3和步骤4之间的相互循环迭代，最终可以得到最优的通行优先权顺序和车辆轨迹的规划方案，进而得到步骤1.5中的最优解，至此完成了高速公路瓶颈区域的协作驾驶问题的求解。
[0165]
以上实施例仅用以说明本技术的技术方案，而非对其限制；尽管参照前述实施例对本技术进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本技术各实施例技术方案的精神和范围，均应包含在本技术的保护范围之内。