一种基于时空图卷积网络的空域扇区复杂度预测方法

1.本发明涉及空中交通环境预测、空中交通管制等技术领域，具体涉及一种基于时空图卷积网络的空域扇区复杂度预测方法。


背景技术：

2.近年来，我国相较于世界大部分地区，在航空量的增长趋势上尤为明显，空管系统面临着十分严峻的挑战。常规的空管体系是以管制员为主体来提供服务的，并将多个空域划分为更细的扇区，每一扇区由一位管制员负责，但复杂的空中交通运作态势会给管制员带来极大负担。一方面，为使扇区内复杂度保持在管制员可承受范围内，管制员会采取战术级流量管制措施如等待或绕飞等，这在一定程度上会造成航班延误；另一方面，由于复杂度等级目前并没有一个确切的计算公式，全由管制专家的经验判断，高维的复杂度特征因子容易让管制员误判，无法做到准确的实时预测，导致扇区内运行安全风险提升，进而引发飞行事故。因此，建立一个智能化系统来预测未来扇区的复杂度，可以大大降低人为的非实时性和不可靠性，并帮助管制员提前做出管制决策，从而实现提前的空中交通动态规划，这是非常有意义的。
3.空域扇区复杂度预测在空中交通管制领域是被广泛研究的课题之一。该课题研究的是：利用n个空域扇区在过去一段连续时间的28维特征因子，通过一定方法提取历史序列的特征，从而预测出未来某时刻空域扇区的复杂度等级(高、中、低)。现有空域扇区复杂度预测技术，如参考文献1：王超,杨乐.空域扇区流量与拥塞预测的概率方法[j].西南交通大学学报,2011,046(001):162-166，依据航空器在扇区内停留时间来建立概率模型，但是没有考虑扇区之间的空间依赖关系，在短时空域复杂度预测上所取得的效果并不好。此外，目前空域扇区复杂度仍大部分人为根据经验判断，具有非实时性和不可靠性。
[0004]
图卷积神经网络(gcn)在最近兴起，其作用的对象是不具备规则空间特征的数据，如推荐系统、电子交易、分子结构等抽象出来的图谱。这些图谱具有拓扑图特征，即一个节点可能与其余多个节点相连，也可能不相连。常规的卷积神经网络在这些不规则的空间结构上不起作用，而gcn通过人为设计卷积核的部分权重，可以有效提取拓扑图的空间特征，并在使用矩阵逼近的相关算法后，高复杂度的图卷积操作被简化为高效的矩阵乘积操作，使得gcn在实时性要求极高的交通流量预测上得以推广。
[0005]
门控卷积神经网络(gated cnn)通过在时间轴上对每一个特征因子序列做一维卷积，并使用glu(gated liner unit)作为激活函数，可以有效提取数据的时间特征，且相比于常规的序列预测网络rnn复杂度更低，反应速度更快。


技术实现要素：

[0006]
针对目前空域扇区复杂度由人为根据经验判断，具有人为的非实时性和不可靠性，而现有技术建立的概率模型在短时空域复杂度预测上所取得的效果较差等问题，本发明提供了一种基于时空图卷积网络的空域扇区复杂度预测方法，基于gcn和gated cnn实现
空域扇区复杂度预测，以解决上述问题。
[0007]
本发明的一种基于时空图卷积网络的空域扇区复杂度预测方法，包括如下步骤：
[0008]
步骤1：获取空域扇区数据集，基于扇区之间的中心距离和航班流量构建扇区的拓扑图；计算扇区的邻接矩阵w，邻接矩阵中元素w
ij
表示扇区i对扇区j的贡献度；
[0009]
步骤2：基于图卷积神经网络和门控卷积神经网络搭建空域扇区复杂度预测模型；
[0010]
所述的预测模型包括两个时空卷积模块、输出层和分类层；所述的时空卷积模块包括两个门控卷积神经网络和一个图卷积神经网络，图卷积神经网络位于两个门控卷积神经网络之间；
[0011]
所述的图卷积神经网络对输入的信号x执行图卷积，提取扇区拓扑特征；所述的门控卷积神经网络，用于提取时间序列特征；第一时空卷积模块的第一门控卷积神经网络输入的信号为n个扇区过去h个连续时刻的复杂度因子；n、h均为正整数；
[0012]
所述的输出层将时空卷积模块的输出数据在时间轴进行归一化，输出预测时间的空域扇区复杂度；
[0013]
所述的分类层对输出层输出的预测序列处理，输出扇区复杂度；
[0014]
步骤3：利用空域扇区数据集对所述的空域扇区复杂度预测模型进行训练，将实时获取的空域扇区的复杂度因子输入训练后的预测模型，预测未来时刻的扇区复杂度。
[0015]
所述的步骤2中，图卷积神经网络执行图卷积表示如下：
[0016]
θ*gx＝θ(l)x＝θ(uλu
t
)x＝uθ(λ)u
t
x
[0017]
其中，*g为图卷积操作符号，θ为图卷积核，l为归一化拉普拉斯矩阵，u是矩阵l的特征向量组成的矩阵，λ是矩阵l的特征值组成的矩阵；利用邻接矩阵w计算归一化拉普拉斯矩阵l；利用切比雪夫逼近得到图卷积核θ。
[0018]
所述的步骤2中，第一时空卷积模块的输出x
″
表示为：
[0019]
x
″
＝γ
′1*
τ
relu(θ
′
*g(γ
′0*
τ
x
′
))
[0020]
其中，x
′
为n个扇区过去h个连续时刻的复杂度因子，γ
′0，γ
′1为上下两个门控卷积神经网络门控卷积层，θ
′
是图卷积核。
[0021]
所述的步骤2中，门控卷积神经网络包含一个一维卷积，特征通道分为两组，一组通道与输入残差连接与另一组通道输入门控线性单元进行激活。
[0022]
本发明的优点与积极效果在于：
[0023]
(1)本发明方法提出了一种空域复杂度的时空预测模型，首次考虑了多扇区之间的空间邻接关系，能够利用图卷积网络充分挖掘空域复杂度的空间特征，提取到空域复杂度在扇区拓扑网络上的传递规律，大大提升对未来空域复杂度的预测效果。
[0024]
(2)本发明方法基于门控卷积神经网络算法，一方面能够更有效地捕捉到空域复杂度在时间周期上的变化特征，提取到长短期混合模式下的时序数据特征，提升预测模型的可靠性；另一方面该模型训练参数较少，计算速度较快，提升了空域复杂度预测的实时性。
[0025]
(3)本发明方法采用深度学习框架，能够自适应地进行空域复杂度预测，避免了人为预测的主观性，这种智能化预测方式能够在实际空管业务中减少人力物力资源的使用，最大化了空管系统的运行效率。
附图说明
[0026]
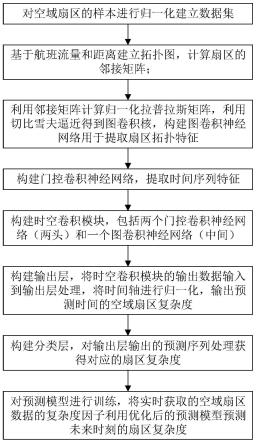
图1是本发明的基于时空图卷积网络的空域扇区复杂度预测方法的流程图；
[0027]
图2是本发明的空域扇区复杂度预测模型的整体结构图；
[0028]
图3是本发明的门控卷积神经网络的结构示意图；
[0029]
图4是本发明的时空卷积模块的结构示意图；
[0030]
图5是本发明的输出层的结构示意图。
具体实施方式
[0031]
下面将结合附图和实施例对本发明作进一步的详细说明。
[0032]
本发明提出的一种基于时空图卷积网络的空域扇区复杂度预测方法，基于扇区之间的中心距离进行拓扑图建模，将gcn提取的扇区拓扑特征与gated cnn提取的多组时间序列特征融合，进行未来扇区复杂度因子预测，并利用多组全连接层对各扇区的复杂度因子进行特征压缩和复杂度等级分类。
[0033]
本发明实施例中，设空域扇区共有n个，采集各空域扇区的历史数据，生成n条训练样本，对每个扇区采用如现有技术一样，每个样本提取28维特征因子，因此，由历史数据得到n个扇区的训练样本表示为xi∈rn×
28
表示第i个样本，包括所有扇区在某时刻的特征因子，x
ij1
表示第i个样本第j个扇区的第1维特征因子。本发明实施例中，空域扇区的复杂度等级有三种：高、中、低。对训练样本添加扇区的独热码复杂度等级标签，标签表示为：其中yi∈rn×3表示第i个样本的所有扇区在某时刻的复杂度等级独热码。特征因子也称为复杂度因子。
[0034]
如图1所示，本发明的基于时空图卷积网络的空域扇区复杂度预测方法，实现主要分如下三大步骤来说明。
[0035]
步骤1，对空域扇区的样本进行归一化处理，然后建立数据集。
[0036]
为防止训练或测试网络时数据值溢出，利用z分数(z-score)的方法进行数据归一化，即对每一个扇区的每一个特征分别归一化，特征的每一个样本均需要减去该扇区中该特征的均值并除以方差。
[0037]
用n个扇区过去h个连续时刻的复杂度因子来预测未来第f时刻的复杂度等级，那么共可打包n-h-f+1条输入数据。规定第一条数据为0时刻，假设当前时刻为t，数据可以表示为：
[0038][0039]
其中，data
t
∈rh×n×
28
表示所有扇区在过去h个连续时刻的复杂度因子。
[0040]
其对应的标签为：
[0041][0042]
其中label
t
∈r1×n×3表示所有扇区在未来第f时刻的复杂度等级。
[0043]
步骤2，基于图卷积神经网络和门控卷积神经网络搭建空域扇区复杂度预测模型。
[0044]
预测模型整体结构如图2所示，本发明实施例预测模型包括两个时空卷积模块、输出层和分类层。其中，时空卷积模块利用图卷积神经网络和门控卷积神经网络组合形成。本
发明实施例中输入预测模型的信号为n个扇区过去h个连续时刻的复杂度因子，针对步骤1所建立的数据集，即为data
t
，t＝h-1,h,
…
n-f-1。本发明实施例模型的搭建具体分如下5个步骤来说明。
[0045]
步骤2.1，构建图卷积神经网络，用于提取扇区拓扑特征。
[0046]
本发明基于谱图卷积的定义引入图卷积操作符号“*g”，图卷积定义为：
[0047]
θ*gx＝θ(l)x＝θ(uλu
t
)x＝uθ(λ)u
t
x
[0048]
其中，θ为图卷积核，l为归一化拉普拉斯矩阵，in是单位矩阵，d∈rn×n为度矩阵，w为邻接矩阵，u∈rn×n是矩阵l的特征向量组成的矩阵，λ∈rn×n是l的特征值组成的矩阵。该定义中，输入的图信号x被一个核θ通过θ和图傅里叶变换u
t
x之间的乘积过滤。
[0049]
步骤2.1.1，首先采用扇区之间的航班流量和航线与扇区相交情况进行拓扑图建模，计算获得邻接矩阵。
[0050]
常规的邻接矩阵是基于节点之间的距离建模，相邻距离较远的节点之间权重较小。而空域扇区并不能仅仅基于这个方法建模，因为不同省的相邻扇区之间由于距离较近，可以采用其他交通方式代替，因此航班数非常少，这意味着这两个扇区之间复杂度相关性很小，矩阵权重应很小，如昆明到贵阳几乎没有航班；而同一省内部的各子扇区之间虽然距离很近，但航空器切换扇区非常频繁，这意味着权重应该很大。根据该实际情况，本发明提出一种基于距离和航班流量的建模方法：
[0051]
近似认为飞机从每个扇区的中心起飞，且从一扇区飞往另一扇区为直线飞行，也即航线为扇区中心的连线。由于航空器只要位于一个扇区内，就会对该扇区复杂度进行贡献，因此扇区i对扇区j的贡献度，也即权重，与扇区i到其余所有扇区的平均航班量均有关系，本发明依据航线在扇区内长度占比来分类权重，建立一个抽象拓扑图结构，具体如下：
[0052]
将飞机起点和终点所在的扇区中心连接，航线由位于扇区内部的各线段拼接而成，设扇区i与扇区k之间距离为m
ik
；z
ikj
为m
ik
位于扇区j内的航线长度，即航线与扇区相交部分；扇区i与扇区j之间的航班流量贡献度定义为：
[0053][0054]
其中，flow
ik
为当前数据集中从扇区i到扇区k的实际航班量，若从扇区i到扇区k的航线未经过扇区j，z
ikj
＝0。距离m
ik
是扇区i与扇区k的中心连线的长度。
[0055]
邻接矩阵w中元素w
ij
定义为：
[0056][0057]
其中，σ2用于控制权重的大小和分布。
[0058]
步骤2.1.2，利用计算的邻接矩阵计算归一化拉普拉斯矩阵。
[0059]
计算度矩阵d，其非对角元素d
ij
＝0(i≠j)，其对角线元素d
ij
为邻接矩阵w对应行元素之和，如下：
[0060][0061]
依据定义，初始化拉普拉斯矩阵l中元素如下：
[0062][0063]
其对角线元素为w每一行之和，其余元素为w的对应位置元素的相反数。
[0064]
利用度矩阵d来归一化拉普拉斯矩阵l：
[0065][0066]
归一化后对角线元素一定为1，其余元素在-1与0之间。
[0067]
步骤2.1.3，利用切比雪夫逼近得到图卷积核。
[0068]
原始的图卷积复杂度为o(n2)，可以通过近似策略降低其复杂度降低至线性，最常用的是切比雪夫逼近。核θ可以被一个关于λ的多项式限制起来，也就是：
[0069][0070]
其中，k表示图卷积核的大小，它决定了卷积从中心节点开始的最大半径；θ∈rk是一个多项式系数的向量，θk是项λk的系数。可以利用切比雪夫多项式对核近似，即：
[0071][0072]
其中λ
max
为矩阵l的最大特征值，in为单位矩阵。
[0073]
因此图卷积可以写为：
[0074][0075]
其中切比雪夫k阶逼近定义为：
[0076][0077]
其中表示归一化后的拉普拉斯矩阵的第k阶逼近矩阵，初始化的第k阶逼近矩阵，初始化
[0078]
在得到图卷积核后，图卷积神经网络利用该卷积核对输入x进行图卷积操作。
[0079]
步骤2.2，构建门控卷积神经网络，用于提取时间序列特征。
[0080]
门控卷积神经网络的时间卷积层包含一个一维卷积，核的宽度为k
t
，将特征通道数一分为二，其中一组通道与输入残差连接后与另一组通道输入门控线性单元glu进行激活，如图3所示。一维卷积作用于拓扑图上每一个扇区节点的时间轴，因此拓扑图的时间卷积可以视为一个有着h(h≤h)个时间轴，n个节点和c个通道的时间序列s∈rh×n×c，卷积核输出其中p和q各占输出的一半通道数，k
t
表示一维卷
积的时间轴个数，即卷积核长度。引入门控卷积运算符“*
τ”，结果可定义为：
[0081][0082]
其中，y为输入信号，第一个时空卷积模块的输入信号为n个扇区过去h个连续时刻的复杂度因子；p和q是glu的输入门，为s的切片，表示对应元素乘积，sigmoid门函数σ(q)控制当前哪个状态输入p，哪个状态输入q，对于发现时间序列中的组成结构和动态方差是相关的。非线性门通过堆叠时间层对挖掘输入也有贡献。除此以外，在堆叠时间卷积层时，实现了残差连接防止梯度消失。
[0083]
步骤2.3，构建时空卷积模块。
[0084]
时空卷积模块包括两个门控卷积神经网络(两头)和一个图卷积神经网络(中间)，如图4所示。采取瓶颈策略让该模块两头通道数少，中间多，形成“三明治”结构。此外，每个时空卷积模块之后会加入一个归一化层和dropout层，防止数据溢出和过拟合。
[0085]
对于时空卷积模块的输入x
′
∈rh×n×c′
，输出可以定义为：
[0086]
x
″
＝γ
′1*
τ
relu(θ
′
*g(γ
′0*
τ
x
′
))
[0087]
其中，x
′
为包含当前时刻的h个历史数据(也即过去的时间轴)，每条数据用含有c
′
个通道的n个扇区节点表示，每经过一个时空卷积模块，其时间轴数量减少2(k
t-1)。特别说明，x
″
在时间轴部分归一之前不具备实际物理意义，时间轴归一后表示预测的未来某一时刻序列。γ
′0，γ
′1为上下两个门控卷积层，θ
′
是图卷积核。relu为线性整流函数。
[0088]
步骤2.4，构建输出层，将时空卷积模块的输出数据输入到输出层处理，将时间轴进行归一化，输出预测时间的空域扇区复杂度。
[0089]
输出层包含两个门控卷积神经网络和一个单独的一维卷积层，如图5所示，将时间轴的数量归一化，输出通道数还原为初始的28，实现了时间和空间的特征融合。设第二时空卷积模块输入到输出层的数据为未来第f时刻的预测序列可以定义为：
[0090][0091]
其中为一维卷积的卷积核，γ
″′0，γ
″′1分别为输出层的两个门控卷积层。预测序列表示未来第f时刻的n个扇区的复杂度因子。
[0092]
步骤2.5，构建分类层，对输出层输出的预测序列处理获得对应的扇区复杂度。
[0093]
分类层包含n组全连接层，每组全连接层有两个隐藏层，用于将预测的每个扇区复杂度因子转换为相应复杂度，相当于管制员对复杂度等级的判断过程。用参数w1,b1,w2,b2表示两个隐藏层的参数，对于预测序列每一扇区的分类结果l
t+f
∈r1×3可定义为：
[0094][0095]
其中为的切片，即某个扇区的未来复杂度因子。
[0096]
步骤3，对预测模型进行训练。本发明实施例进行训练是包括如下步骤3.1和3.2。
[0097]
步骤3.1，模型训练时代价函数的设置。
[0098]
本发明实施例，代价函数中采用交叉熵损失函数，在输出为概率分布时它对损失
更加敏感。再加入l2正则化损失，防止模型过拟合。对于分类结果l
t+f
∈r1×3和真实标签某一扇区的损失lossj可定义为：
[0099][0100]
总损失loss
total
定义为：
[0101][0102]
其中，λ表示正则化因子，w
trainable
表示所有可训练参数。
[0103]
步骤3.2，模型训练的配置。
[0104]
本发明实施例的数据包大小batch_size设置为16，训练20轮，采用adam优化器，学习率初始为0.01，每5轮衰减90％，损失函数正则化因子设置为0.0001。
[0105]
利用步骤1获得的训练数据集对预测模型进行训练，得到参数优化后的预测模型，则可以将实时获取的空域扇区数据的复杂度因子输入预测模型，预测未来时刻的扇区复杂度。
[0106]
除说明书所述的技术特征外，均为本专业技术人员的已知技术。本发明省略了对公知组件和公知技术的描述，以避免赘述和不必要地限制本发明。上述实施例中所描述的实施方式也并不代表与本技术相一致的所有实施方式，在本发明技术方案的基础上，本领域技术人员不需要付出创造性的劳动即可做出的各种修改或变形仍在本发明的保护范围内。