一种自动驾驶汽车驶离环形交叉口的极限轨迹的确定方法

1.本发明属于自动驾驶轨迹规划领域，具体为一种自动驾驶汽车驶离环形交叉口的极限轨迹的确定方法。


背景技术：

2.环形交叉口在我国各类城市中普遍存在，其不仅增加了城市绿化面积，还能有效减少低交通量情况下的道路拥挤、车辆延误以及交通事故发生率，在缓解城市交通问题上起到了积极作用。
3.由于自动驾驶技术的快速发展，自动驾驶汽车的适用场景由相对简单的路况开始向复杂的城市环形交叉口场景扩展。现有对环形交叉口中行驶的自动驾驶汽车的研究多倾向于智能交通仿真领域与基于环道选择的轨迹规划。发明专利202110280449.8将环形交叉口划分为入环区、环中区和出环区，通过采集入环区各仿真车辆的交通参数值，根据预设的换道规则构建仿真车辆入环路径目标曲线；发明专利202111074077.x基于b样条插值法进行全局路径规划，通过制定驶入和驶出规则进行合理的环道选择。然而，未见对自动驾驶汽车驶离环形交叉口的极限轨迹的研究。环形交叉口车流交织程度高，若未在适当区域做出转向操作，汽车将难以在遵守交通规则的前提下安全驶入出口道。
4.基于上述背景，自动驾驶汽车在环形交叉口这种对驾驶技术要求较高的场景中行驶时，为保证其安全、顺利地驶出环形交叉口，需要对其行驶轨迹进行合理、精细地规划，计算出环道内的最晚驶离转向点，以此来对自动驾驶汽车开始向出口道方向转向的区域作出限制。


技术实现要素：

5.一种自动驾驶汽车驶离环形交叉口的极限轨迹的确定方法，包括：从任一环道n最晚驶离转向点an，出口道的道路中心线或渠化线的端点b，以及点an、点b之间的极限轨迹anb；
6.自动驾驶汽车，下称汽车，其左侧车头沿环道n中心线所在的圆曲线行驶，n＝1，2
…
n，车头方向垂直于中心岛半径方向；
7.汽车驶出环岛的过程为非受限自由换道，即此过程不受其他汽车影响；
8.环道n最晚驶离转向点an位于自动驾驶汽车左侧车头，且位于环道n中心线所在的圆曲线；
9.极限轨迹anb按照自动驾驶汽车换道或转弯行驶时所采用的五次多项式计算；
10.一种自动驾驶汽车驶离环形交叉口的极限轨迹的确定方法，其步骤如下：
11.步骤一：将环形交叉口中心岛与环道线均视为正圆形的同心圆，中心岛的圆心为o，半径为r，单位：米；建立以中心岛圆心o为原点的直角坐标系，以自动驾驶汽车的目标出口道中心线为y轴，远离o点的方向为y轴正方向，与y轴正方向顺时针垂直90
°
的方向为x轴的正方向；
12.步骤二：自动驾驶汽车左侧车头沿环道n中心线所在的圆曲线在步骤一所述的直角坐标系中的方程为其中，d为环道宽度，单位：米；
13.步骤三：以等角度间隔1
°
在汽车当前位置与y轴之间的环道n中心线所在的圆曲线上取点，任意点i的坐标为(xi，yi)，其中i＝1，2，3
…
m，(xm，ym)为最晚驶离转向点an的坐标；
14.步骤四：出口道的道路中心线或渠化线的端点b在步骤一所述的直角坐标系中的坐标为(0，r+nd)；
15.步骤五：以环道n的中心线作为参考线，分别以参考线的切向向量和法向向量所在直线为坐标轴建立frenet坐标系，采用五次多项式模型描述换道轨迹：
[0016][0017]
式中，t代表换道过程中的某一时刻，单位：秒；s(t)、d(t)分别表示frenet坐标系下纵向位移和横向位移关于时间t的函数，单位：米；pk、qk分别表示t的系数，k＝0，1，2，3，4，5；
[0018]
对s(t)函数进行二次求导：
[0019][0020]
式中，表示t时刻汽车的纵向速度，单位：米/秒，表示t时刻汽车的纵向加速度，单位：米/平方秒；
[0021]
将汽车左侧车头驶离环道n中心线的时刻记为t0＝0，带入s(t)函数，求得前三项系数：
[0022][0023]
对d(t)函数进行二次求导：
[0024][0025]
式中，表示t时刻汽车的横向速度，单位：米/秒，表示t时刻汽车的横向加速度，单位：米/平方秒；
[0026]
将汽车左侧车头驶离环道n中心线的时刻记为t0＝0，带入d(t)函数，求得前三项系数：
[0027][0028]
步骤六：以任意点i处汽车左侧车头驶离环道n中心线的时刻为t0，令i＝1，通过直角坐标系与frenet坐标系的转换求得(x1，y1)在frenet坐标系下的纵向位移s(0)，求得p0、p1和p2；
[0029]
定义任意点i处出发的汽车左侧车头到达b点的时刻为换道结束时刻t
1i
，即i＝1时，t
1i
＝t
11
；令t＝t
11-t0，其中t为换道时间，取值范围为[3，10]，单位：秒；则b点在frenet坐标系下的纵向位移为s(t
11
)，目标出口道上汽车的纵向期望速度和纵向期望加速度为和
[0030]
将t
11
时刻状态信息带入s(t)函数，求得系数p3、p4和p5；
[0031]
再通过直角坐标系与frenet坐标系的转换求得(x1，y1)在frenet坐标系下的横向位移d(0)，求得q0、q1和q2；
[0032]
b点在frenet坐标系下的横向位移为d(t
11
)，目标出口道上汽车的横向期望速度和期望加速度为和
[0033]
将t
11
时刻状态信息带入d(t)函数，求得系数q3、q4和q5，
[0034]
得到frenet坐标系下的五次多项式换道轨迹；
[0035]
步骤七：换道过程中，汽车受自身、道路等相关条件的约束，分别为：
[0036]
约束一：汽车自身约束
[0037][0038]
式中，vs为汽车的横向速度，单位：米/秒；v
s，limit
为横向速度极限，单位：米/秒；as为横向加速度，单位：米/平方秒；a
s，limit
为横向加速度极限，单位：米/平方秒；vd为纵向速
度，单位：米/秒；v
d，limit
为纵向速度极限，单位：米/秒；ad为纵向加速度，单位：米/平方秒；a
d，-limit
为纵向减速度极限，单位：米/平方秒；a
d，limit
为纵向加速度极限，单位：米/平方秒；
[0039]
约束二：道路约束
[0040]
v≤v
l，limit
[0041]
式中，v为汽车横向速度与纵向速度矢量和，单位：米/秒；v
l，limit
为道路速度限制，单位：米/秒；
[0042]
步骤八：分别令i＝2，3，4
…
，重复步骤六直至在t的取值范围内轨迹方程无解，令m＝i-1，此时的(xm，ym)即为环道n最晚驶离转向点an，求得的轨迹anb即为自动驾驶汽车驶离环形交叉口的极限轨迹。
[0043]
与现有技术相比，本发明的有益效果是：
[0044]
本发明所述的一种自动驾驶汽车驶离环形交叉口的极限轨迹的确定方法，考虑了自动驾驶汽车在环形交叉口出环时环境条件的限制，计算出驶离环形交叉口的极限轨迹和最晚驶离转向点，为环形交叉口中行驶的自动驾驶汽车提供最晚出环转向预警，为自动驾驶汽车轨迹规划提供技术支持。
附图说明
[0045]
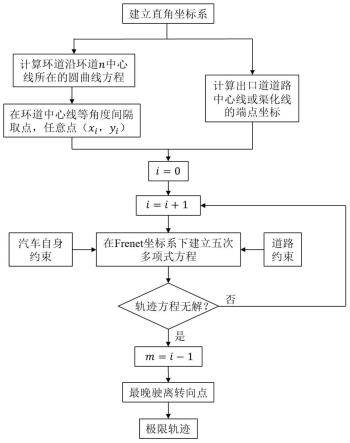
图1为本发明所述的自动驾驶汽车驶离环形交叉口的极限轨迹的计算方法总体流程图；
[0046]
图2为本发明所述的frenet坐标系示意图；
[0047]
图3为本发明实施例所述的正阳广场环形交叉口的结构化示意图；
[0048]
图4为本发明实施例所述的任意点i、道路中心线端点、最晚驶离转向点以及极限轨迹示意图。
具体实施方式
[0049]
本发明专利所述的一种自动驾驶汽车驶离环形交叉口的极限轨迹的确定方法，适用于不受周围车辆干扰的自动驾驶汽车即将驶离环形交叉口的情境。通过计算极限轨迹和最晚驶离转向点向汽车发出最晚转向预警，以避免违反交通规则，实现汽车自身安全行驶。
[0050]
参阅图1，本发明所述的一种自动驾驶汽车驶离环形交叉口的极限轨迹的确定方法有以下几个步骤：
[0051]
步骤一：建立以中心岛圆心为原点、自动驾驶汽车的目标出口道中心线为y轴的直角坐标系；
[0052]
步骤二：计算环道沿环道n中心线所在的圆曲线方程；
[0053]
步骤三：以等角度间隔在汽车当前位置与y轴之间的环道n中心线所在的圆曲线上取点；
[0054]
步骤四：计算出口道道路中心线或渠化线的端点坐标；
[0055]
步骤五：建立frenet坐标系下的五次多项式，求得前三项系数；
[0056]
步骤六：在换道时间约束下用换道结束时刻状态信息求出五次多项式其余系数，得到五次多项式换道轨迹；
[0057]
步骤七：加入汽车自身约束和道路约束；
[0058]
步骤八：依次在所有点重复步骤六直至五次多项式轨迹方程无解，此时最后一个有解的点即为最晚驶离转向点，其对应的方程轨迹即为自动驾驶汽车驶离环形交叉口的极限轨迹。
[0059]
实施例
[0060]
下面将结合本技术实施例中的附图，对本发明的详细内容和本技术实施例中的技术方案进行清楚、完整地描述。所描述的实施例仅是本技术一部分实施例，而不是全部的实施例。基于本技术中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本技术保护的范围。
[0061]
正阳广场为5路交叉的5环道环形交叉口，出口道湖西路为双向四车道，道路中心线上置有隔离护栏，正阳广场环形交叉口的结构化示意图如图3所示。
[0062]
如图4所示，以正阳广场中心岛的圆心为原点o建立直角坐标系，以湖西路为自动驾驶汽车的目标出口道，湖西路道路中心线为y轴，远离o点的方向为y轴正方向，与y轴正方向顺时针垂直90
°
的方向为x轴的正方向。
[0063]
环道n中心线所在的圆曲线在直角坐标系中的方程为：
[0064][0065]
通过高精地图获取环形交叉口结构参数。中心岛半径r为33米，环道宽度d为5米，环道数n＝1，2，3，4，5。
[0066]
如图4所示，以等角度间隔1
°
在所在的曲线上取点，任意点i的坐标为(xi，yi)，其中i＝1，2，3
…
m。
[0067]
湖西路的道路中心线的端点b的坐标为(0，58)。
[0068]
以图4中所示环道3为例，以环道3的中心线作为参考线，采用参考线的切向向量和法向向量建立frenet坐标系，采用五次多项式模型计算环道3到湖西路出口道的极限轨迹：
[0069][0070]
令i＝1，通过直角坐标系与frenet坐标系的转换求得(x1，y1)在frenet坐标系下的纵向位移s(0)和横向位移d(0)。
[0071]
分别对s(t)、d(t)函数进行二次求导并将t0＝0代入，求得s(t)、d(t)的前三项系数
[0072][0073]
定义任意点i处出发的汽车左侧车头到达b点的时刻为换道结束时刻t
1i
，即i＝1，t
1i
＝t
11
；令t＝t
11-t0，其中t为换道时间，取值范围为[3，10]，单位：秒；则b点在frenet坐标
系下的纵向位移为s(t
11
)，目标出口道上汽车的纵向期望速度和期望加速度为和b点在frenet坐标系下的横向位移为d(t
11
)，目标出口道上汽车的横向期望速度和期望加速度为和
[0074]
将t
11
时刻状态信息带入s(t)函数，带入s(t)函数，带入d(t)函数，求得系数p3、p4、p5、q3、q4和q5，
[0075]
得到frenet坐标系下的五次多项式换道轨迹。
[0076]
分别令i＝2，3，4
…
，重复步骤六直至在t的取值范围内轨迹方程无解，令m＝i-1，此时的(xm，ym)即为环道n最晚驶离转向点an，求得的轨迹anb即为自动驾驶汽车驶离环形交叉口的极限轨迹。
[0077]
计算出的极限轨迹如图4所示。
[0078]
将极限轨迹计算方法应用于环形交叉口任一自动驾驶汽车，将其仿真结果与未应用此计算方法的汽车仿真结果做对比，发现应用此计算方法的汽车驶出环形交叉口时压线行驶等违反交通规则的现象消失，汽车平均行驶时间减少了8.9％，说明此自动驾驶汽车驶离环形交叉口的极限轨迹确定方法保证了行车安全，行车效率明显提高。