一种并联式六自由度副面调整机构设计工艺的制作方法
本发明属于射电望远镜天线装置领域,具体涉及到一种并联式六自由度天线副面调整机构系统的设计工艺。
背景技术:
随着现代电子技术、无线电通信、雷达技术、计算机技术的迅猛发展。射电天文技术方法得到长足的进步。作为射电天文主要探测工具的射电望远镜,口径越来越大,且要求其精度越来越高。随着天线口径的增大,副面越来越重,其撑杆变形越来越大,由于受重力变形及安装误差的影响,主反射面的位置和姿态安装精度存在一定的误差,从而影响了天线的接收性能。因此需要在副面和撑杆之间安装调整机构,对于精度要求较高的天线系统,尤其是大型射电天线由于副反射面直径大、自重大、所需调整量大、而且需要进行多个自由度的调整,故高精度射电天线的副反射面位姿调整机构需要具备高刚度、结构紧凑、精度高、多个自由度调整等性能,此时传统的主反射面位姿调整机构已不能满足使用要求。
六自由度并联机构由于其刚度高、自重小、自由度多很适合作为副面调整机构。而传统的六自由度并联机构一般为结构对称,它在z轴方向刚度最大,而大型射电望远镜天线在工作时一般不朝天,因此需要研究适合于大型射电望远镜天线的副面调整机构。
技术实现要素:
针对上述所提及的传统副面调整机构存在的诸多不足,提供了一种并联式六自由度驱动副面调整机构的设计工艺,以补偿因重力变形和安装误差等因素导致的天线性能的变化和指向偏差,使其具有高的指向精度、环境适应性以及长期工作的可靠性,提高天线设备的信号接收性能。
对此提供的技术方案为:
一种并联式六自由度副面调整机构设计工艺,包括以下步骤,
s1.定义天线各个铰点坐标,六个杆的分支铰点在上平台坐标系中的坐标bi=(xiyizi)(i=1…6),六个杆的分支铰点在下平台坐标系中的坐标ai=(xiyizi)(i=1…6),共计36个参数,所述参数根据空间结构分为n1-ni组;
s2.建立构型,由上述参数中初始位置时n1组所对应参数设立为初始构型,采用运动学反解计算初始构型所对应杆长,该构型的初始杆长li0和所需要的最大杆长lmax;
s3.判断是否满足约束条件,设定分支杆两端的固定件部分所预留的安装长度为l,判断是否满足li0>l+3lmax,若不满足li0>l+3lmax,则返回步骤s2计算下一组直至满足li0>l+3lmax;
s4.将该构型下允许的动平台动作范围进行分组,分组方式为动平台位于各个不同位姿状态下的位置所对应的坐标,得到离散化的m1-mi组;
s5.计算各杆受力,
由m1组开始,根据力平衡方程计算求解m1下的六个杆的受力f=[f1f2f3f4f5f6]t,计算完成后计算下一组直至得到mi组的六个杆的受力;
s6.将天线俯仰角渐变增加,增加量为*,*取值范围为1度-10度,每次天线俯仰角增加后重复执行步骤s4-s5,直至得到天线仰角为90度时的各杆受力得到0度-90度状态下m1-mi组对应的六杆受力;
s7.计算下一空间结构分组n所对应的0度-90度状态下m1-mi组对应的六杆受力,直至完成ni的计算,将所有计算结果组成受力模型库;
s8.判断最佳构型,选取受力模型库中力刚度矩阵最大所对应的构型n作为最优构型;
s9.加工分支杆和上平台(4)、下平台(5),根据最优构型n进行加工得到对应分支杆的长度,并将分支杆对应的配装至上平台(4)、下平台(5)之间。
进一步的,所述的步骤s2的计算初始构型所对应杆长的计算方法为,
定义下平台的三个欧拉角为α、β、γ,则从下平台到上平台的旋转变化矩阵为:
进一步的,所述的步骤s5的求解m1下的六杆受力过程为,
利用螺旋理论建立数学模型。当以力旋量表示六个轴力时,考虑动平台的平衡,六个杆的力螺旋之和应与平台的六维力相平衡,列出螺旋方程:
式中,f={fx,fy,fz,mx,my,mz}t为作用在动平台上的六维外力,f=[f1f2f3f4f5f6]t,为各分支杆上所受的力,
进一步的,步骤s8中力刚度矩阵为六杆受力最大值最小且受力均衡所对应的矩阵模型。
与现有技术比较具有的有益效果在于:
通过采用了针对大型天线的设计工艺,摒弃了传统的对称式六杆结构,本机构的杆列采用非对称的的杆结构分布,补偿因重力变形和安装误差等因素导致的天线性能的变化和指向偏差,使其具有高的指向精度、环境适应性以及长期工作的可靠性,提高天线设备的信号接收性能。
本机构可以灵活地指向工作空间内的任意方向,实现副面调整机构工作空域内任意姿态的连续调整。
将得到的全部分支杆受力进行分析,运用综合优化方法将各个姿态下的六个分支杆综合计算得出该位姿下机构分支受力的综合值,综合值包括各构型下六个分支受力总和、六个分支受力最大值和最小值差等优化数据,综合优化所有分支受力值,找出天线在最佳仰角下各分支受力值最优的构型,该构型作为天线副面调整机构的构型,可以选出针对不同的天线所选取的最佳构型天线结构,其刚度最大,耐久性最高,在天线最佳仰角时基本保持或者接近垂直状态。。
附图说明
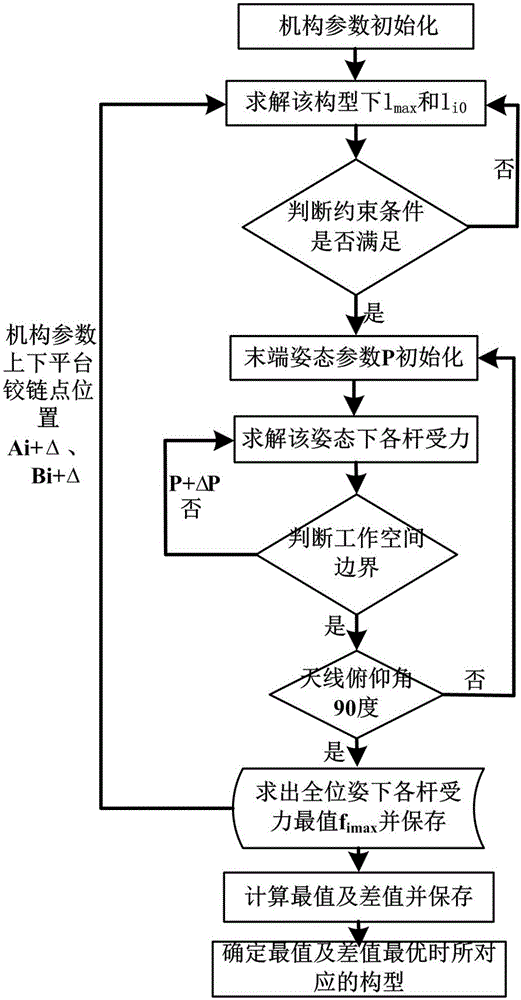
图1为构型优化设计工艺
图2为天线最佳仰角示意图;
图中的附图标记为:天线主反射体—1、天线副反射体—2、天线副面撑杆—3、调整机构上平台—4、调整机构下平台—5、分支杆—6、虎克铰—7、球铰—8、调整机构—9、护管—10。
具体实施方式
如图2所示,一种大型射电望远镜并联式六自由度调整机构系统,包括上平台4、下平台5、分支杆6、、虎克铰7、球铰—8。所述的上平台4连接在天线副面撑杆3上,所述的下平台5连接在天线副反射体2上,所述的分支杆6通过虎克铰7与上平台4连接、通过球铰8与下平台5连接,所述的上平台联结在射电望远镜天线副面撑杆上,所述的下平台连接在副面上,上平台和下平台之间通过六个运动分支连接,且六个分支不完全对称分布。
如图2所示,所述的六条运动支链结构完全相同,但长度不同,每个分支上的虎克铰7和球铰8的位置通过图1的设计工艺确定。
所述的分支杆6的直线运动实现方式可以为直线运动电机,或者为液压缸、滚珠丝杠机构等在添加动力源之后以实现直线运动。
如图1所示,其设计工艺为:
s1.,而传统六自由度并联机构一般在天线仰角为0度时刚度最好,因此需要在构型设计时考虑天线工作的最佳仰角,首先定义天线各个铰点坐标,六个杆的分支铰点在上平台坐标系中的坐标bi=(xiyizi)(i=1…6),六个杆的分支铰点在下平台坐标系中的坐标ai=(xiyizi)(i=1…6),六个杆体铰接点,每个杆体上下端两个坐标点,每个坐标点横纵竖,共计36个参数,所述参数根据空间结构分为n1-ni组,空间结构认定,人工预设为位移量,设备越大位移量越大,设备越小位移量越小,选取好位移量后,即可将所述分组分出;
s2.建立构型,由上述参数中初始位置时n1组所对应参数设立为初始构型,采用运动学反解计算初始构型所对应杆长,计算初始构型所对应杆长的计算方法为,
定义下平台的三个欧拉角为α、β、γ,则从下平台到上平台的旋转变化矩阵为:
s3.判断是否满足约束条件,设定分支杆两端的固定件部分所预留的安装长度为l,判断是否满足li0>l+3lmax,若不满足li0>l+3lmax,则返回步骤s2计算下一组直至满足li0>l+3lmax;
s4.将该构型下允许的动平台动作范围进行分组,分组方式为动平台位于各个不同位姿状态下的位置所对应的坐标,得到离散化的m1-mi组;
s5.计算各杆受力,
由m1组开始,根据力平衡方程计算求解m1下的六个杆的受力
求解m1下的六杆受力过程为,
利用螺旋理论建立数学模型。当以力旋量表示六个轴力时,考虑动平台的平衡,六个杆的力螺旋之和应与平台的六维力相平衡,列出螺旋方程:
式中,f={fx,fy,fz,mx,my,mz}t为作用在动平台上的六维外力,f=[f1f2f3f4f5f6]t,为各分支杆上所受的力,
得到六杆受力f=[f1f2f3f4f5f6]t,计算完成后计算下一组直至得到mi组的六个杆的受力;
s6.将天线俯仰角渐变增加,增加量为α,α取值范围为1度-10度,每次天线俯仰角增加后重复执行步骤s4-s5,直至得到天线仰角为90度时的各杆受力得到0度-90度状态下m1-mi组对应的六杆受力;
s7.计算下一空间结构分组n所对应的0度-90度状态下m1-mi组对应的六杆受力,直至完成ni的计算,将所有计算结果组成受力模型库;
s8.判断最佳构型,选取受力模型库中力刚度矩阵最大所对应的构型n作为最优构型,力刚度矩阵为六杆受力最大值最小且受力均衡所对应的矩阵模型。
s9.加工分支杆和上平台(4)、下平台(5),根据最优构型n进行加工得到对应分支杆的长度,并将分支杆对应的配装至上平台(4)、下平台(5)之间。
。
- 还没有人留言评论。精彩留言会获得点赞!