燃料电池低温环境启动控制系统

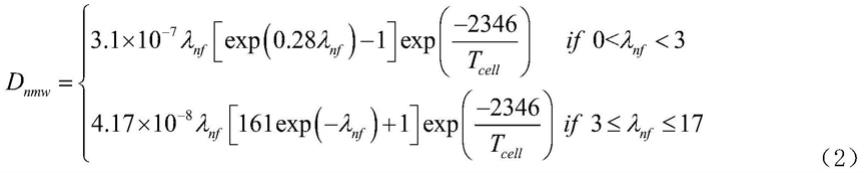
1.本发明属于燃料电池汽车优化控制技术领域。


背景技术：

2.我国宣布将力争于2030年前实现二氧化碳排放达到峰值、2060年前实现碳中和。氢能是替代化石能源实现双碳目标的重要选择，它已经成为应对气候变化、建设脱碳社会的重要能源。2021年中国氢电产业发展蓝皮书指出，2030
‑
2035年实现氢能及燃料电池汽车的大规模应用。工业和信息化部也提出，到2035年我国公共领域用车将全面实现电动化，燃料电池汽车实现商业化应用。
3.当燃料电池处于零度以上环境时，电堆反应生成的水可被直接回收，用于后续工作过程中的加湿工作或直接排出。若燃料电池从零度以下的环境中启动，且工作在大电流工况下或工作时间较长时，由于此时电堆温度还未升至零上，反应生成的水无法被直接排出或利用，它会由液态相变至固态，即产生冰。冰的存在对电堆输出特性会产生不利影响：若冰完全将催化层或气体扩散层覆盖，电堆将无法继续正常工作，此时冷启动失败。低温环境下燃料电池汽车的冷启动问题是影响其商业推广的重要因素。如何在电堆完全被冰覆盖之前将温度升温至冰融化点即零度是目前学者们较为关注的热点问题。燃料电池冷启动分为内部升温和辅助升温两种方式，其中内部升温细分为三种方式，分别为改变输出特性法，氧饥饿法与催化法。电堆辅助升温方面，主要有冷却液加热、热气体吹扫与反向电压加热三种方式。
4.针对燃料电池低温环境的启动方法，主要有以下问题：1.辅助升温方式增加了系统的成本和复杂程度并使得燃料电池整体系统可靠性降低。
5.2.目前关于燃料电池低温环境启动的解决方法大多集中在开环设置燃料电池工作点方面，即为燃料电池设置某一固定的电流或电压，使其始终工作在该固定点从而实现冷启动，未能针对被控系统从全局进行优化设计。
6.3.温升速率与结冰速率的关系往往是导致冷启动失败的关键原因，换言之，在冰体积分数达到1即冰将催化层与气体扩散层等完全覆盖之前，若电堆温度未升至0℃(摄氏度)，则冷启动失败。但目前已经存在的燃料电池低温环境启动方法仅考虑能否成功升温至0℃，而未考虑冷启动过程中升温速率与结冰速率的关系，一味的追求温升速率可能会导致冷启动失败。


技术实现要素：

7.本发明的目的是在约束电流变化率的前提下通过平衡温升速率与结冰速率之间的关系，规划冷启动过程中的电流轨迹，实现燃料电池在期望启动时间内冷启动的燃料电池低温环境启动控制系统。
8.本发明步骤是：
s1、建立燃料电池冷启动系统微观模型1.1建立燃料电池水传递模型1.1.1膜中非冻结水含量模型式(1)为膜中非冻结水质量守恒方程，等式左侧表示膜中非冻结水含量动态变化，等式右侧第一项表示气体扩散项，第二项表示源项：分别来自于氧化还原反应生成的水、膜中非冻结水与气态水之间的相变、膜中非冻结水与固态水之间的相变以及电液拖拽其中，ρ
mem
表示膜密度，ew表示膜当量，ω表示催化层中离子交联聚合物的体积分数，λ
nf
表示膜中非冻结水含量，表示*对x的二阶偏导，x表示非冻结水在膜中的扩散距离；式(1)中d
nmw
表示膜中非冻结水扩散系数其中，t
cell
表示电堆温度；式(1)中s
nmw
表示膜中非冻结水的源项其中，j
c
表示阴极催化层反应速率，f表示法拉第常数；式(3)中s
n
‑
v
表示膜中非冻结水与气态水之间的相变过程其中，表示膜中非冻结水与气态水之间的变化速率系数，式(4)中λ
equil
表示平衡水含量，即膜在内外处于水平衡状态时的水含量：式(5)中a表示水活度其中，x
vp
表示孔隙中气态水摩尔分数，p
g
表示孔隙中混合气体压强，p
sat
表示水蒸气饱和压力，表示液态水体积分数；式(3)中s
n
‑
i
表示膜中非冻结水与固态水之间的相变过程
其中，表示膜中非冻结水与冰之间的变化速率系数，λ
sat
表示饱和水含量式(3)中s
eod
表示氢离子通过离子交联聚合体时对水分子的拖拽现象其中，n
d
表示电液拖拽系数，即每个氢离子通过离聚体所拖拽的水分子数，由式(10)获得，表示修正离子电导率，由式(11)获得，表示离子电势表示离子电势其中，k
ion
表示离子交联聚合体电导率；1.1.2膜中冻结水含量模型式(12)为膜中冻结水质量守恒方程，等式左侧表示膜中冻结水含量λ
f
的动态变化，等式右侧表示源项其中，s
fmw
表示膜中冻结水的源项其中，s
n
‑
f
表示膜中冷冻水向膜中非冻结水变化的过程，表示膜中非冻结水与膜中冻结水之间相变速率系数；1.1.3液态水含量模型式(14)为液态水质量守恒方程，等式左侧表示液态水体积分数动态变化，等式右侧第一项表示扩散项，第二项表示液态水源项其中，ε表示孔隙率，ρ
lq
表示液态水密度，表示液态水体积分数，d
lq
表示液态水
扩散率， s
lq
表示液态水源项s
lq
＝s
v
‑
l
‑
s
l
‑
i
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)式(15)中s
v
‑
l
表示气态水与液态水的相变过程其中，γ
cond
表示冷凝速率系数，γ
evap
表示蒸发速率系数，表示水的摩尔质量，r表示气体常数；式(15)中s
l
‑
i
表示液态水与固态水的相变过程其中，γ
fusn
表示凝固速率系数，γ
melt
表示融化速率系数，ρ
lq
表示液态水密度，ρ
ice
表示冰密度，表示冰体积分数；1.1.4冰含量模型式(18)为冰质量守恒方程，等式左侧表示冰体积分数的动态变化，等式右侧表示冰的源项式(18)中s
ice
为冰的源项式(19)中s
l
‑
i
与s
n
‑
i
由式(17)与式(7)得到，s
v
‑
i
表示气态水与固态水的相变过程其中，γ
desb
表示凝华速率系数；1.2建立燃料电池温升模型比热方程q＝cmδt，其中，q表示物体温度变化过程中吸收或放出的热量，c表示物体比热容，m表示物体摩尔质量，δt表示物体温度变化量，燃料电池热量产生与散失的关系以及温度变化如公式(21)所示其中，c
st
表示电堆比热容，m
st
表示电堆质量，c
ice
表示冰比热容，m
ice
表示冷启动过程中冰质量，其值与冰体积分数有关，表示电堆温度对时间的微分；
式(21)中q
tot
表示电堆总化学能其中，δh表示氢气与氧气发化学反应生成水的焓变，表示阳极参与反应的氢气物质的量其中，n表示电堆中电池片数，i
st
表示电堆电流值；式(21)中p
st
表示电堆输出功率p
st
＝nv
cell
i
st
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(24)其中，v
cell
表示电堆输出电压；式(21)中q
amb
表示电堆向环境散热能量其中，t
amb
表示环境温度，η
heat
表示边界散热系数，a
st
表示电堆表面积；1.3建立燃料电池输出电压模型v
cell
＝e
nernst
‑
v
act
‑
v
ohmic
‑
v
conc
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(26)式(26)中能斯特电压e
nernst
式(26)中活化压降v
act
其中，α表示传递系数，i表示电流密度，j
*
表示交换电流密度，δ
cl
表示催化层厚度，ξ表示化学计量比，p
c
表示毛细压力，c
ref
表示参考摩尔浓度；式(26)中欧姆压降v
ohmic
其中，asr
bp
、asr
gdl
、asr
mem
、asr
cl
分别表示双极板、气体扩散层、膜、催化层的面比电阻；式(26)中浓差压降v
conc
其中，δ
gdl
表示气体扩散层厚度，δ
cl
表示催化层厚度，与分别表示气体扩散层与催化层的有效扩散系数，c
h
表示等效阴极氢摩尔浓度；s2、建立冷启动电流优化2.1建立冷启动电流优化选取燃料电池电堆温度t
cell
与启动电流i
st
作为状态变量，选取电流变化率di
st
作为控制量，通过对燃料电池冷启动系统工作原理的分析，得到其状态方程为：式(31)通过公式(32)表示：其中f1表示电堆温度变化与电堆温度，非冻膜水含量，电堆电流与电堆电流变化率的函数关系，f2表示电堆电流变化与电堆电流变化率的函数关系；优化目标是满足终端约束与电流变化率约束的条件下，使得燃料电池在平衡结冰速率与温升速率之间找到一组电流值完成冷启动；其中，j表示优化问题的性能指标，φ(x(t
f
))表示对状态变量的终端约束，t0与t
f
分别表示起始时刻与终值时刻，u表示控制量，即di
st
，ω1，ω2为加权系数，u是控制变量取值的集合； 2.2确定冷启动电流优化1)出于对电堆的保护，需要满足燃料电池启动过程中电流的变化率约束：di
stmin
≤di
st
(t)≤di
stmax
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(34)其中，di
stmin
表示燃料电池电流变化率最小值，di
stmax
表示燃料电池电流变化率最大值；2)需要满足燃料电池冷启动系统的动态方程：3)需要满足燃料电池冷启动系统的状态约束：
其中，t
cellmin
与i
stmin
分别表示电堆温度与电堆电流的最小值，t
cellmax
与i
stmax
分别表示电堆温度与电堆电流的最大值，t
cellini
与i
stini
分别表示电堆温度与电堆电流在初始时刻t0的值，t
cellfinal
与 i
stfinal
分别表示电堆温度与电堆电流在终止时刻t
f
的值，即终端约束；s3、设计基于dp的启动电流规划方法求解出能够使得燃料电池成功实现冷启动的最优电堆电流i
st
轨迹3.1dp的电堆电流轨迹优化需要对数据进行采样，将该环境温度下的冷启动时间离散成n
m
等份，离散时间记为 k∈{1,2,...,n
m
+1}，目标函数为：其中，u表示满足约束的电流变化率集合，φ(x(n
m
+1))表示状态变量的终端约束，δt表示燃料电池相邻两状态间的采样时间间隔，控制变量u(k)表示相邻采样时间内的电流变化量，将电堆温度在初始时刻的值设定为环境温度，将电堆温度在终值时刻的值设定为0℃，需要满足的具体约束条件是：1)出于对电堆的保护，需要满足燃料电池启动过程中电流的变化率约束：δi
stmin
≤δi
st
(k)≤δi
stmax
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(38)其中，δi
st
表示电流变化率，δi
stmin
表示燃料电池电流变化率最小值，δi
stmax
表示燃料电池电流变化率最大值；2)需要满足燃料电池冷启动系统的动态方程：3)需要满足燃料电池冷启动系统的状态约束：
3.2划分关于系统状态及控制变量的网格将状态变量电堆温度t
cell
从环境温度t
amb
开始以每格0.65℃的增幅递增至0℃，以环境温度为
ꢀ‑
13℃为例，划分出20个状态网格，将状态变量电堆电流i
st
从0a开始以每格6a的增幅递增至150a，划分出25个状态网格；将控制量电流变化率从
‑
3a/s开始以每格1a/s的增幅递增到5a/s，划分出9个控制变量网格；3.3代价成本经划分网格完成的状态变量x(k)分别在控制变量网格u(k)中各u
i
(k)作用下，依据状态转移方程得到新的状态变量x(k+1)；从初始时刻起，控制变量网格中的不同控制量对状态变量网格中的不同状态量进行作用，进而得到下一时刻的状态变量网格以及相应的一组代价j(k)，此过程重复进行，直至启动时间终值；每一时刻不同状态量在不同控制量作用下的代价成本 j(k)可由公式(41)得出，并将该代价成本j(k)按时间顺序从前至后进行存储3.4确定最优决策从终端时刻开始，满足状态变量的终端约束，即确定了状态变量在k＝n
m
+1时刻的值，电堆温度与电堆电流分别取值为t
cellfinal
与i
stfinal
，即x(n
m
+1)，对应初始代价成本j(n
m
+1)＝0，从终端时刻的前一时刻开始代价成本公式(42)所示其中，j
*
(k)表示第k时刻系统中状态变量为x(k)时的代价成本最优值，即升温速率，结冰速率，电流变化率之间加权作差的最大值，l(x(k),u(k))表示第k时刻状态变量值处在x(k) 时系统经控制作用u(k)作用后产生的代价转移成本，j
*
(k+1)为上一时刻系统中状态变量为 x(k+1)时的代价转移成本最大值，将每一时刻得到最大代价成本对应的状态变量进行顺序组合，得到最优状态变量序列{x
*
(1),x
*
(2),...,x
*
(k)}，即最优的电堆温度t
cell
序列与电堆电流 i
st
序列
9.本发明是主要针对燃料电池低温环境启动问题，基于动态规划算法(dynamic programming,dp)设计启动电流轨迹全局优化方法。采用内部升温方式，在满足燃料电池电堆电流变化率的约束条件下，计算从0a(安培)开始变化的启动电流轨迹。仿真结果表明所设计的控制系统能够较好的平衡温升速率与结冰速率之间的关系，提高燃料电池的冷启动性能并解决现有技术中三点问题。本发明的有益效果是：1.设计了燃料电池低温环境启动控制系统。相较于现有冷启动方法，本发明提出了基于模型框架下的优化控制策略，在期望启动时间内基于dp优化出一组电堆电流轨迹，
与传统的开环控制策略相比，所提出的控制策略可以在保证冷启动成功的同时缩短冷启动时间；2.结合燃料电池实际应用中的启动过程，对燃料电池启动电流的变化率加以约束，避免因电流变化过大而影响燃料电池安全性能。同时使燃料电池启动过程中的电流从零开始升高，相较于传统启动方法中启动初始时刻电流值较大的情况更贴合实际工作过程。
附图说明
10.图1为燃料电池低温环境启动控制系统简图。图2为燃料电池低温环境启动控制系统工作流程图。图3为冷启动过程中电流对电堆温度影响示意图。图4为dp算法所得电流。图5为计算处理所得电流与时间的关系图。图6为恒流法电流与dp所得电流在冷启动过程中对电堆温度影响对比图。图7为恒流法电流与dp所得电流在冷启动过程中对电堆冰体积分数影响对比图。
具体实施方式
11.本发明包括以下步骤：步骤一：建立燃料电池冷启动系统微观模型，具体包括水传递模型，燃料电池温升模型，燃料电池输出电压模型。
12.步骤二：建立冷启动电流优化问题描述。确定冷启动电流优化问题约束条件。
13.步骤三：结合环境温度，设计基于动态规划算法的启动电流规划方法。在保证满足系统终端约束及电流变化率约束的条件下，以平衡温升速率与结冰速率之间的关系为目标，设计基于dp的电流优化策略，求解出期望启动时间下的最优启动电流轨迹。
14.步骤四：将上述dp求解得到的电流序列进行数据处理，得到电流与时间的关系，并传递至燃料电池电子控制单元用于实时控制。
15.步骤五：对所设计燃料电池低温环境启动控制系统进行仿真验证。
16.下面结合附图对本发明做进一步详细描述：本发明的燃料电池低温环境启动控制系统简图如图1所示。具体实施方式为：建立燃料电池微观模型，具体包括燃料电池水传递模型、燃料电池温升模型、燃料电池输出电压模型。建立冷启动电流优化问题的问题描述，确定其约束条件。在满足系统终端约束和电流变化率约束的条件下，通过平衡升温需求与结冰速率之间的关系，应用dp算法求解出期望启动时间内对应的电流轨迹。将上述求解结果进行数据处理，得到电流与时间的关系轨迹并将其作为最优控制序列传送给相应的执行控制单元用于实时控制。最后对所设计的系统进行仿真验证，佐证其对燃料电池低温环境冷启动性能的改善情况。
17.燃料电池低温环境启动控制系统工作流程如图2所示，具体包括以下步骤：1.建立燃料电池冷启动系统微观模型建立质子交换膜燃料电池(proton exchange membrane fuel cell，pemfc)电堆的冷启动微观模型。该模型考虑了冷启动过程中催化层内水的主要运输与相变现象，电堆
温升过程以及催化层结冰对输出电压的影响。
18.步骤1包含以下子步骤：1.1建立燃料电池水传递模型鉴于燃料电池工作过程中，氢气与氧气进行氧化反应后生成的水大多存在于阴极内，所以在该模型中，主要对催化层(catalyst layer,cl)内水的相变及传输过程进行建模。同时存在以下守恒方程：催化层膜中非冻结水质量守恒方程、催化层膜中冻结水质量守恒方程、液态水质量守恒方程、冰质量守恒方程。
19.1.1.1膜中非冻结水含量模型膜中非冻结水质量守恒方程如公式(1)所示，等式左侧表示膜中非冻结水含量动态变化，等式右侧第一项表示气体扩散项，第二项表示源项：分别来自于氧化还原反应生成的水、膜中非冻结水与气态水之间的相变、膜中非冻结水与固态水之间的相变以及电液拖拽。其中，ρ
mem
表示膜密度，ew表示膜当量，ω表示催化层中离子交联聚合物的体积分数，λ
nf
表示膜中非冻结水含量，表示*对x的二阶偏导，x表示非冻结水在膜中的扩散距离， d
nmw
表示膜中非冻结水扩散系数，s
nmw
表示膜中非冻结水的源项。
20.公式(1)中d
nmw
表示膜中非冻结水扩散系数，其表达式如下式所示：其中，t
cell
表示电堆温度。
21.公式(1)中s
nmw
表示膜中非冻结水的源项，其表达式如下式所示：其中，j
c
表示阴极催化层反应速率，f表示法拉第常数，s
n
‑
v
表示膜中非冻结水与气态水之间的相变过程，s
n
‑
i
表示膜中非冻结水与固态水之间的相变过程，s
eod
表示氢离子通过离子交联聚合体时对水分子的拖拽现象。
22.公式(3)中s
n
‑
v
表示膜中非冻结水与气态水之间的相变过程，其表达式如下式所示：其中，表示膜中非冻结水与气态水之间的变化速率系数，λ
equil
表示平衡水含量，即膜在内外处于水平衡状态时的水含量。
23.λ
equil
表达式如公式(5)所示：
其中，a表示水活度。
24.a表达式如公式(6)所示。其中，x
vp
表示孔隙中气态水摩尔分数，p
g
表示孔隙中混合气体压强，p
sat
表示水蒸气饱和压力，表示液态水体积分数。
25.公式(3)中s
n
‑
i
表示膜中非冻结水与固态水之间的相变过程，其表达式如下式所示：其中，表示膜中非冻结水与冰之间的变化速率系数，λ
sat
表示饱和水含量。
26.λ
sat
表达式如式(8)所示
27.公式(3)中k表示温度单位：开尔文，s
eod
表示氢离子通过离子交联聚合体时对水分子的拖拽现象，其表达式如下式所示：其中，n
d
表示电液拖拽系数，即每个氢离子通过离聚体所拖拽的水分子数，表示修正离子电导率，表示离子电势。
28.n
d
表达式如公式(10)所示，表达式如公式(11)所示表达式如公式(11)所示其中，k
ion
表示离子交联聚合体电导率。
29.1.1.2膜中冻结水含量模型膜中冻结水质量守恒方程如公式(12)所示，等式左侧表示膜中冻结水含量λ
f
的动态变化，等式右侧表示源项，来自于膜中非冻结水与膜中冻结水之间的转变其中，s
fmw
表示膜中冻结水的源项。
30.s
fmw
表达式如式(13)所示。其中，s
n
‑
f
表示膜中冷冻水向膜中非冻结水变化的过程。表示膜中非冻结水与膜中冻结水之间相变速率系数。
31.1.1.3液态水含量模型液态水质量守恒方程如公式(14)所示，等式左侧表示液态水体积分数动态变化，等式右侧第一项表示扩散项，第二项表示液态水源项，来自于水的三相之间的变化其中，ε表示孔隙率，ρ
lq
表示液态水密度，表示液态水体积分数，d
lq
表示液态水扩散率， s
lq
表示液态水源项。
32.s
lq
表达式如公式(15)所示。s
lq
＝s
v
‑
l
‑
s
l
‑
i
，
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)其中，s
v
‑
l
表示气态水与液态水的相变过程，s
l
‑
i
表示液态水与固态水的相变过程。
33.公式(15)中s
v
‑
l
表示气态水与液态水的相变过程，其表达式如下式所示：其中，γ
cond
表示冷凝速率系数，γ
evap
表示蒸发速率系数，表示水的摩尔质量，r表示气体常数，值为8.314j
·
(mol
·
k)
‑1。
34.公式(15)中s
l
‑
i
表示液态水与固态水的相变过程，其表达式如下式所示：其中，γ
fusn
表示凝固速率系数，γ
melt
表示融化速率系数，ρ
lq
表示液态水密度，ρ
ice
表示冰密度，表示冰体积分数。
35.1.1.4冰含量模型冰质量守恒方程如公式(18)所示，等式左侧表示冰体积分数的动态变化，等式右侧表示冰的源项。其中，s
ice
为冰的源项，来自于气态水与液态水凝结成冰以及非冻结水析出结冰。s
ice
表达式如公式(19)所示
36.公式(19)中s
l
‑
i
与s
n
‑
i
可由公式(17)与公式(7)计算得出，s
v
‑
i
表示气态水与固态水的相变过程，表达式如下式所示：其中，γ
desb
表示凝华速率系数。
37.1.2建立燃料电池温升模型燃料电池冷启动策略成功的标准为在电堆被冰完全覆盖之前将其升温至零度以上，所以对温度模块进行建模是很有必要的。基于比热方程q＝cmδt，其中，q表示物体温度变化过程中吸收或放出的热量，c表示物体比热容，m表示物体摩尔质量，δt表示物体温度变化量，燃料电池热量产生与散失的关系以及温度变化如公式(21)所示。其中，c
st
表示电堆比热容，m
st
表示电堆质量，c
ice
表示冰比热容，m
ice
表示冷启动过程中冰质量，其值与冰体积分数有关，表示电堆温度对时间的微分。q
tot
表示电堆总化学能， p
st
表示电堆输出功率，q
amb
表示电堆面向环境的散热能量。
38.公式(21)中q
tot
表示电堆总化学能，其表达式如下式所示：其中，δh表示氢气与氧气发化学反应生成水的焓变，表示阳极参与反应的氢气物质的量。
39.表达式如下式所示：其中，n表示电堆中电池片数，i
st
表示电堆电流值。
40.公式(21)中p
st
表示电堆输出功率，其表达式如下式所示：p
st
＝nv
cell
i
st
，
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(24)其中，v
cell
表示电堆输出电压。
41.公式(21)中q
amb
表示电堆向环境散热能量，其表达式如下式所示：其中，t
amb
表示环境温度，η
heat
表示边界散热系数，a
st
表示电堆表面积。
42.1.3建立燃料电池输出电压模型据上节所述，电堆输出功率与电堆输出电压有关，故需要对输出电压进行建模。输
出电压通过能斯特电压e
nernst
与活化压降v
act
、欧姆压降v
ohmic
、浓差压降v
con
作差得到，如式(25)所示。v
cell
＝e
nernst
‑
v
act
‑
v
ohmic
‑
v
conc
，
ꢀꢀꢀꢀꢀꢀ
(26)其中，能斯特电压e
nernst
与电堆温度、氧气分压以及氢气分压有关，活化压降v
act
与常温环境不同的是它会受到冰体积分数的影响。欧姆压降v
ohmic
与电堆双极板、气体扩散层、催化层膜的面比电阻以及电流有关，浓差压降v
con
主要受电流密度与氢气浓度影响。
43.公式(26)中能斯特电压e
nernst
表达式如下式所示：
44.公式(26)中活化压降v
act
表达式如下式所示：其中，α表示传递系数，i表示电流密度，j
*
表示交换电流密度，δ
cl
表示催化层厚度，ξ表示化学计量比，p
c
表示毛细压力，其值与液态水体积分数有关，c
ref
表示参考摩尔浓度。
45.公式(26)中欧姆压降v
ohmic
表达式如下式所示：其中，asr
bp
、asr
gdl
、asr
mem
、asr
cl
分别表示双极板、气体扩散层、膜、催化层的面比电阻。
46.公式(26)中浓差压降v
conc
表达式如下式所示：其中，δ
gdl
表示气体扩散层厚度，δ
cl
表示催化层厚度，与分别表示气体扩散层与催化层的有效扩散系数，c
h
表示等效阴极氢摩尔浓度。
47.2建立冷启动电流优化问题描述选取控制变量，建立冷启动电流优化问题描述，确定约束条件。
48.2.1建立冷启动电流优化问题描述冷启动过程中燃料电池电流对电堆温度影响如图3所示，当电堆以大电流启动时
升温速率较高，然而由于堆内冰累积速率与电流值成正比，所以此时电堆会快速地被冰覆盖，进而导致冷启动失败。当电堆以小电流启动时，结冰速度较慢，电堆不易完全被冰覆盖，但此时升温速率相对较小，故升温时间较长。由上述分析可知，在导致冷启动失败的大电流和启动时间过长的小电流之间，存在一组合适的电流值使其成功实现较短时间的冷启动。
49.燃料电池冷启动成功的标志为在冰完全将催化层等结构覆盖之前将电堆温度升至0℃，故电堆温度与电堆冰含量是两个需要被重点关注的变量，而电堆冰含量主要与电流值相关，所以本文选取燃料电池电堆温度t
cell
与启动电流i
st
作为状态变量，选取电流变化率δi
st
作为控制量。通过对燃料电池冷启动系统工作原理的分析，得到其状态方程为：
50.上式可以通过公式(32)表示：其中f1表示电堆温度变化与电堆温度，非冻膜水含量，电堆电流与电堆电流变化率的函数关系，f2表示电堆电流变化与电堆电流变化率的函数关系。
51.优化目标是满足终端约束与电流变化率约束的条件下，使得燃料电池在平衡结冰速率与温升速率之间找到一组电流值完成冷启动：其中，j表示优化问题的性能指标，φ(x(t
f
))表示对状态变量的终端约束，t0与t
f
分别表示起始时刻与终值时刻，u表示控制量，即di
st
，ω1，ω2为加权系数，u是控制变量取值的集合。
52.2.2确定冷启动电流优化问题约束条件低温环境燃料电池冷启动系统需满足如下约束条件：1)出于对电堆的保护，需要满足燃料电池启动过程中电流的变化率约束：di
stmin
≤di
st
(t)≤di
stmax
,
ꢀꢀꢀꢀꢀꢀꢀꢀ
(34)其中，di
stmin
表示燃料电池电流变化率最小值，di
stmax
表示燃料电池电流变化率最大值；
53.2)需要满足燃料电池冷启动系统的动态方程：
54.3)需要满足燃料电池冷启动系统的状态约束：
其中，t
cellmin
与i
stmin
分别表示电堆温度与电堆电流的最小值，t
cellmax
与i
stmax
分别表示电堆温度与电堆电流的最大值，t
cellini
与i
stini
分别表示电堆温度与电堆电流在初始时刻t0的值，t
cellfinal
与 i
stfinal
分别表示电堆温度与电堆电流在终止时刻t
f
的值，即终端约束。
55.3.设计基于dp的启动电流规划方法结合环境温度信息与期望启动时间，在约束电流变化率的前提下以平衡冷启动过程中温度升高速率与结冰速率为优化目标，求解出能够使得燃料电池成功实现冷启动的最优电堆电流i
st
轨迹具体包含以下步骤：
56.3.1基于dp的电堆电流轨迹优化问题描述基于dp的电堆电流i
st
轨迹规划在保证满足系统终端约束与电流变化率约束的条件下以平衡冷启动过程中温度升高速率与结冰速率为优化目标进行优化求解。在求解过程中，需要对数据进行采样，将该环境温度下的冷启动时间离散成n
m
等份，离散时间记为k∈{1,2,...,n
m
+1}，目标函数为：其中，u表示满足约束的电流变化率集合，φ(x(n
m
+1))表示状态变量的终端约束，δt表示燃料电池相邻两状态间的采样时间间隔，控制变量u(k)表示相邻采样时间内的电流变化量。将电堆温度在初始时刻的值设定为环境温度，将电堆温度在终值时刻的值设定为0℃。
57.需要满足的具体约束条件是：1)出于对电堆的保护，需要满足燃料电池启动过程中电流的变化率约束：δi
stmin
≤δi
st
(k)≤δi
stmax
，
ꢀꢀꢀꢀꢀꢀꢀ
(38)其中，δi
st
表示电流变化率，δi
stmin
表示燃料电池电流变化率最小值，δi
stmax
表示燃料电池电流变化率最大值；
58.2)需要满足燃料电池冷启动系统的动态方程：
59.3)需要满足燃料电池冷启动系统的状态约束：
60.3.2划分关于系统状态及控制变量的网格为了应用dp方法，将状态变量电堆温度t
cell
从环境温度t
amb
开始以每格0.65℃的增幅递增至 0℃，以环境温度为
‑
13℃为例，划分出20个状态网格，将状态变量电堆电流i
st
从0a开始以每格6a的增幅递增至150a，划分出25个状态网格；将控制量电流变化率从
‑
3a/s(安培每秒)开始以每格1a/s的增幅递增到5a/s，划分出9个控制变量网格。
61.3.3计算代价成本上述经划分网格完成的状态变量x(k)分别在控制变量网格u(k)中各u
i
(k)作用下，依据状态转移方程得到新的状态变量x(k+1)。从初始时刻起，控制变量网格中的不同控制量对状态变量网格中的不同状态量进行作用，进而得到下一时刻的状态变量网格以及相应的一组代价 j(k)。此过程重复进行，直至启动时间终值。每一时刻不同状态量在不同控制量作用下的代价成本j(k)可由公式(41)计算得出，并将该代价成本j(k)按时间顺序从前至后进行存储，
62.3.4确定最优决策确定最优的控制输入序列需要通过从后向前迭代计算实现。优化问题的优化目标为满足终端约束的条件，使得燃料电池在平衡结冰速率与温升速率之间找到一组电流完成冷启动，并且考虑到电堆安全问题还需要使电流变化率尽可能小。首先从终端时刻开始，满足状态变量的终端约束，即确定了状态变量在k＝n
m
+1时刻的值(电堆温度与电堆电流分别取值为t
cellfinal
与 i
stfinal
)，即x(n
m
+1)，对应初始代价成本j(n
m
+1)＝0，从终端时刻的前一时刻开始代价成本公式(42)所示。其中，j
*
(k)表示第k时刻系统中状态变量为x(k)时的代价成本最优值，即升温速率，结冰速率，电流变化率之间加权作差的最大值。l(x(k),u(k))表示第k时刻状态变量值处在x(k) 时系统经控制作用u(k)作用后产生的代价转移成本。j
*
(k+1)为上一时刻系统中状态变量为 x(k+1)时的代价转移成本最大值。将每一时刻得到最大代价成本对应的状态变量进行顺序组合，得到最优状态变量序列{x
*
(1),x
*
(2),...,x
*
(k)}，即最优的电堆温度t
cell
序列与电堆电流 i
st
序列
63.4.数据处理对最优电堆电流序列进行数据处理，得到用以实时控制策略的电堆电流序列，该
电流序列是时间的函数，如图5所示。
64.5.对所设计燃料电池低温环境启动控制系统进行仿真验证。根据仿真结果，可以看出本发明所提出的燃料电池低温环境启动方法具有如下优越性：1)所设计的燃料电池低温环境启动方法既满足了冷启动过程中电堆温度升高的需求，又考虑了电堆在零度以下环境中阴极反应生成水易结冰的问题。该方法解决了单方面追求温升速率而导致结冰速率过快造成的冷启动失败与单方面追求冷启动成功而导致的启动时间过长的问题。
65.图4为
‑
13℃dp算法所得电流，图6为恒流法电流与dp所得电流在冷启动过程中对电堆温度影响对比图。图7为恒流法电流与dp所得电流在冷启动过程中对电堆冰体积分数影响对比图。从这两组仿真结果可以看出，启动电流大小为150a时，升温速率最快，然而因为此时结冰速率也较为快速，未能在冰体积分数到达1之前将电堆升温至零摄氏度，故启动失败。启动电流大小为50a时，冰累积速率较慢，故其可以在电堆完全被冰覆盖之前升温至0℃，成功完成冷启动，相应的，其升温速率也较为缓慢，故启动时间较长。当采用动态规划法时，电堆的升温速率与结冰速率均处于中间水平，可以在冰体积分数达到1之前，以较快速度将电堆升温至零摄氏度。
66.2)所设计的燃料电池低温环境启动方法得到的启动电流值从0a缓慢上升，相较于传统恒流法，更加符合实际应用中电堆启动过程中电流的变化情况。同时所设计的方法对电流变化速率加以限制，避免电流变化频繁与变化幅度过大而导致的燃料供给响应不及时的问题，满足厂商对电堆保护的要求，满足其安全性能。